「HNSDFZ暑期集训测试1」「LuoguT36488」连连看

题目描述

给定一个n × m的矩形地图，每个各自上可能为空，可能有牌，牌上有一个数字。

对于两张同样数字的牌，如果我们可以在地图上用不超过三根水平或竖直，在地图界内，且不经过其他牌的线段将两张牌连起来，那么我们这一对牌是可以被消去的。

比如下图中，两张1可以被消去，但是2和3都不能被消去。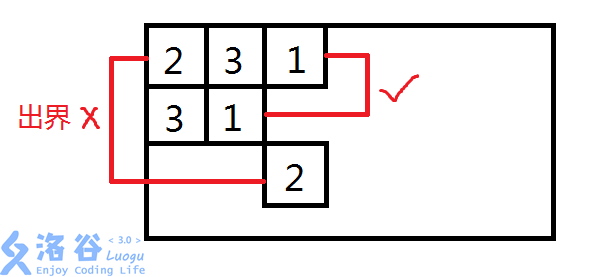

现在给出一个n × m的连连看地图，其中有2k张牌，保证每张牌上的数字都在[1, k]范围内，且每个数字都只会出现两次，问目前有多少对牌是可以消去的。

输入输出格式

输入格式：

输入第一行三个正整数n, m, k，分别代表地图的长，宽以及牌的对数。

接下来k行每行四个正整数x1 , y1 , x2 , y2，表示数字为k的两张牌的位置。

输出格式：

输出仅一行一个整数，表示当前可以消去的牌的对数

输入输出样例

输入样例#1：复制

输出样例#1：复制

说明

30%的数据 n, m≤ 20，k<=min(3, ⌊ n*m/2 ⌋)

接下来30%的数据 n, m≤ 100，k<=min(100, ⌊ n*m/2 ⌋)

接下来30%的数据 n, m≤ 1000，k<=min(5000, ⌊ n*m/2 ⌋)

题解

考虑数据范围很小，我们可以做各种n方操作。

读入的同时把相应坐标标记

    flag[ i ] [ j ]=1;

套两个for循环，分别求横排上的前缀和及竖排上的前缀和

    for(int i=1;i<=n;++i)

    for(int j=1;j<=m;++j)

    ss[i][j]=ss[i-1][j]+tu[i][j],

    hs[i][j]=hs[i][j-1]+tu[i][j];

对于每组牌：

我们把一张牌分别向上下左右暴力走，走到边界或障碍就停，经过的点就标记。（画十字）

|____________|

|      O     |

|      |  O  |

|      |     |

|   O——O————O|

|      |     |

|      |     |

|  O   |     |

|______|_____|

然后把第二张牌也上下左右暴力走，同样经过则标记。如果有到被标记过的点，说明路线相交了，这对牌可消，flag=1

若未相交：

从1~n枚举横坐标j，如果这一段（< x1 , j >点到 < x2 , j >点）上的区间和为0
且< x1 , j >点和< x2 , j >点被标记过(画十字的时候经历过)的话（用前缀和O(1)查询）
则这一段没有障碍，可以连线，flag=1

从1~n枚举纵坐标i，如果< i , y1 >点到< i , y2 >上的区间和为0，则可连，flag=1

最后如果flag为1，则ans++

代码：//考场代码

 #include<algorithm>

 #include<iostream>

 #include<cstring>

 #include<cstdio>

 #include<cmath>

 using namespace std;

 inline int read()//快读

 {

     char ch=getchar();

     int x=;bool s=;

     while(ch<''||ch>''){if(ch=='-')s=;ch=getchar();}

     while(ch>=''&&ch<=''){x=x*+ch-;ch=getchar();}

     return s?x:-x;

 }

 int lx[],ly[],rx[],ry[];

 int ss[][];

 int hs[][];

 bool tu[][];

 bool sf[][];

 int main()

 {

     int n=read(),m=read(),k=read();

     for(int i=;i<=k;++i)

     {

         lx[i]=read(),

         ly[i]=read(),

         rx[i]=read(),

         ry[i]=read();

         tu[lx[i]][ly[i]]=;

         tu[rx[i]][ry[i]]=;//标记

     }

     for(int i=;i<=n+;++i)

     tu[i][]=tu[i][m+]=;

     for(int i=;i<=m+;++i)

     tu[][i]=tu[n+][i]=;

     for(int i=;i<=n;++i)

     for(int j=;j<=m;++j)

     ss[i][j]=ss[i-][j]+tu[i][j],

     hs[i][j]=hs[i][j-]+tu[i][j];//前缀和

     int ans=;

     for(int c=;c<=k;++c)

     {

         int flag=;

         memset(sf,,sizeof(sf));

         //以下一大堆为画十字

         tu[lx[c]][ly[c]]=;

         tu[rx[c]][ry[c]]=;//便于之后操作

         int x=lx[c],y=ly[c];

         int l,r,u,d;

         while(!tu[x][y]){sf[x--][y]=;}

         u=x+;

         x=lx[c]+,y=ly[c];

         while(!tu[x][y]){sf[x++][y]=;}

         d=x-;

         x=lx[c],y=ly[c]-;

         while(!tu[x][y]){sf[x][y--]=;}

         l=y+;

         x=lx[c],y=ly[c]+;

         while(!tu[x][y]){sf[x][y++]=;}

         r=y-;

         x=rx[c],y=ry[c];

         while(!tu[x][y]){if(sf[x][y])flag++;sf[x--][y]=;}

         u=max(u,x+);

         x=rx[c]+,y=ry[c];

         while(!tu[x][y]){if(sf[x][y])flag++;sf[x++][y]=;}

         d=min(d,x-);

         x=rx[c],y=ry[c]-;

         while(!tu[x][y]){if(sf[x][y])flag++;sf[x][y--]=;}

         l=max(l,y+);

         x=rx[c],y=ry[c]+;

         while(!tu[x][y]){if(sf[x][y])flag++;sf[x][y++]=;}

         r=min(r,y-);

         //画十字结束

         if(!flag)

         {

             int zx=lx[c],zy=ly[c],yx=rx[c],yy=ry[c];

             if(zx>yx)swap(zx,yx);

             if(zy>yy)swap(zy,yy);

             for(int i=u;i<=d;++i)//枚举横坐标

             if(hs[i][yy]-hs[i][zy-]==)flag++;

             for(int j=l;j<=r;++j)//枚举纵坐标

             if(ss[yx][j]-ss[zx-][j]==)flag++;

         }

         if(flag)ans++;

         tu[lx[c]][ly[c]]=;

         tu[rx[c]][ry[c]]=;//复原

         //cout<<flag<<endl;

     }

     cout<<ans;//强大怪！！！

     return ;

 }

//强大怪！！！（滑稽