【UOJ34】高精度乘法（FFT）

题意：

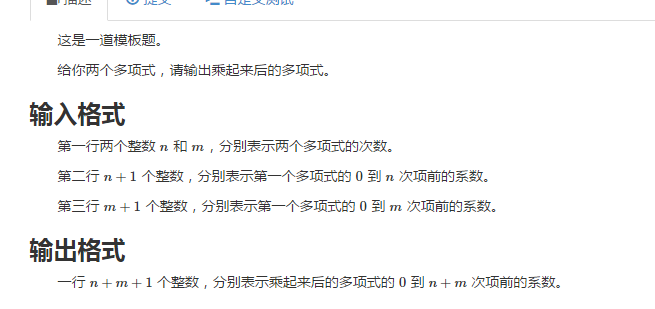
思路：FFT模板，自带10倍常数

 type cp=record
          x,y:double;
         end;
      arr=array[..]of cp;
 var a,b,cur:arr;
     n,m,n1,n2,i,j:longint;
     x:double;

 function jia(a,b:cp;f:longint):cp;
 begin
  if f=- then
  begin
   b.x:=-b.x; b.y:=-b.y;
  end;
  jia.x:=a.x+b.x;
  jia.y:=a.y+b.y;
 end;

 function mult(a,b:cp):cp;
 begin
  mult.x:=a.x*b.x-a.y*b.y;
  mult.y:=a.x*b.y+a.y*b.x;
 end;

 procedure swap(var x,y:cp);
 var t:cp;
 begin
  t:=x; x:=y; y:=t;
 end;

 function max(x,y:longint):longint;
 begin
  if x>y then exit(x);
  exit(y);
 end;

 procedure fft(var a:arr;n,f:longint);
 var i,j,k,m:longint;
     w,u,v:cp;

 begin
  i:=n>>; j:=;
  while j<n do
  begin
   if i<j then swap(a[i],a[j]);
   k:=n>>;
   while k and i> do
   begin
    i:=i xor k;
    k:=k>>;
   end;
   i:=i xor k;
   inc(j);
  end;
  m:=;
  while m<=n do
  begin
   w.x:=cos(*pi*f/m); w.y:=sin(*pi*f/m);
   cur[].x:=; cur[].y:=;
   for i:= to m- do cur[i]:=mult(cur[i-],w);
   i:=;
   while i<n do
   begin
    j:=i;
    while j<i+(m>>) do
    begin
     u:=a[j]; v:=mult(a[j+(m>>)],cur[j-i]);
     a[j]:=jia(u,v,);
     a[j+(m>>)]:=jia(u,v,-);
     inc(j);
    end;
    i:=i+m;
   end;
   m:=m<<;
  end;
 end;

 begin
  assign(input,'uoj34.in'); reset(input);
  assign(output,'uoj34.out'); rewrite(output);
  readln(n1,n2);
  inc(n1); inc(n2);
  for i:= to n1- do
  begin
   read(x); a[i].x:=x;
  end;
  for i:= to n2- do
  begin
   read(x); b[i].x:=x;
  end;
  n:=max(n1,n2);
  m:=;
  while m<=(n<<) do m:=m<<;
  fft(a,m,); fft(b,m,);
  for i:= to m do a[i]:=mult(a[i],b[i]);
  fft(a,m,-);
  for i:= to n1+n2- do write(round(a[i].x/m),' ');
  close(input);
  close(output);
 end.