Coin Toss(uva 10328,动态规划递推,限制条件,至少转至多,高精度)

有n张牌，求出至少有k张牌连续是正面的排列的种数。（1=<k<=n<=100)

Toss is an important part of any event. When everything becomes equal toss is the ultimate decider. Normally a fair coin is used for Toss. A coin has two sides head(H) and tail(T). Superstition may
 work in case of choosing head or tail. If anyone becomes winner choosing head he always wants to choose head. Nobody believes that his winning chance is 50-50. However in this problem we will deal with a fair coin and n times tossing of such a coin. The result
 of such a tossing can be represented by a string. Such as if 3 times tossing is used then there are possible 8 outcomes.

HHH HHT HTH HTT THH THT TTH TTT
As the coin is fair we can consider that the probability of each outcome is also equal. For simplicity we can consider that if the same thing is repeated 8 times we can expect to get each possible sequence
 once.
The Problem
In the above example we see 1 sequnce has 3 consecutive H, 3 sequence has 2 consecutive H and 7 sequence has at least single H. You have to generalize it. Suppose a coin is tossed n times. And the same
 process is repeated 2^n times. How many sequence you will get which contains a consequnce of H of length at least k.

The Input
The input will start with two positive integer, n and k (1<=k<=n<=100). Input is terminated by EOF.
The Output
For each test case show the result in a line as specified in the problem statement.
Sample Input

4 1
4 2
4 3
4 4
6 2

Sample Output

15
8
3
1
43

 

/*
思路:
ps(a数组内部的递推计算本来应该也用高精度整数来计算,但是被我省略了,因为太懒了)
(把至少k个正面)转换为(至多n个正面)-(至多k-1个正面)
对于(至多n个正面),它等于2^n,考虑到n比较大,用高精度大整数来计算出2^n

对于(至多k-1个正面)
先根据k-1是否为0定义f[1][1]的初始值
f[1][2]肯定为1
ps.数组的第二维中1代表正,2代表反的总情况数
由于对反面牌没有要求,所以:
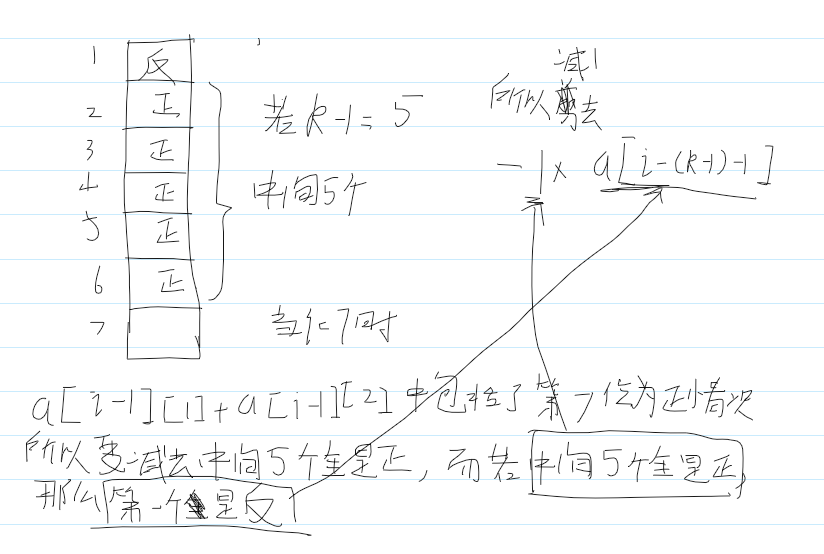
第i次为反情况数=第i-1次为正情况数+第i-1次为反情况数

如果i<=k-1,随便放,那么第i次为正情况数=第i-1次为正情况数+第i-1次为反情况数

如果i=(k-1)+1,那么第i次为正情况数=第i-1次为正情况数+第i-1次为反情况数-1
那个-1是减去前面全是正面的情况


如果i>(k-1)+1,那么第i次为正情况数=第i-1次为正情况数+第i-1次为反情况数-第i-(k-1)-1次为反情况数
那个-第i-(k-1)-1次为反情况数 是排除第i-(k-1)-1次为反而且中间全是正的情况的情况

*/
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const ll maxn=;
ll a[maxn][];
ll big[maxn];
int main()
{
    ll n,k;
    cin>>n>>k;
    big[]=;
    big[]=;
    for(ll i=;i<=n;i++)
    {
        for(ll i=;i<=big[];i++)
            big[i]*=;
        for(ll i=;i<=big[];i++)
        {
            if(big[i]>=)
            {
                big[i+]+=big[i]/;
                big[i]%=;
            }
            if(big[big[]+]>)
                big[]++;
        }
    }

    if(k-==)
    {
        a[n][]=,a[n][]=;
        goto dog;
    }

    a[][]=;a[][]=;
    for(ll i=;i<=n;i++)
    {
        a[i][]=a[i-][]+a[i-][];

        if(i<=k-)
            a[i][]=a[i-][]+a[i-][];
        else if(i==k-+)
            a[i][]=a[i-][]+a[i-][]-;
        else
            a[i][]=a[i-][]+a[i-][]-a[i-(k-)-][];
    }
    dog:;
    big[]-=a[n][]+a[n][];
    while(big[]<)
    {
        big[]+=pow(,big[]-);
        big[big[]]--;
        if(big[big[]]==)
        {
            big[]--;
        }
    }
    for(ll i=;i<=big[];i++)
    {
        if(big[i]>=)
        {
            big[i+]+=big[i]/;
            big[i]%=;
        }
        if(big[big[]+]>)
            big[]++;
    }
    for(ll i=big[];i>=;i--)
        printf("%lld",big[i]);
    return ;
}