字典(trie)树--从入门到入土

今天再来认识一个强大的数据结构。

字典树又称单词查找树，Trie树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。

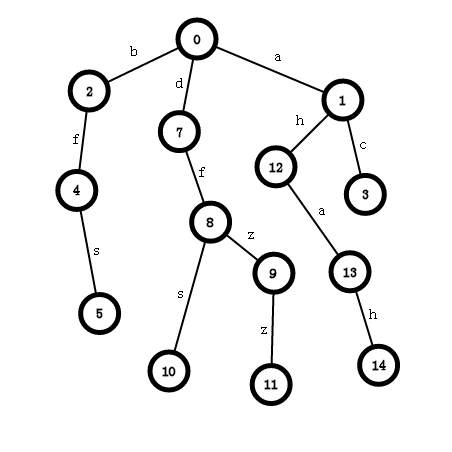
就像这么一棵树，0号点为根节点，这里的节点编号没有多大意义。

看到这棵树首先要注意到这可树上储存的元素(也就是字母)都是储存在树的边上，而不是节点上，节点只是为了让父亲节点知道自己的儿子节点是多少号，便于向下深入。

定义一个二维数组tree[i][j]，表示第i个节点与tree[i][j]之间的边储存着j (好难解释啊qwq)，举个例子就好明白了：

看上图，tree[1]['b']=2,tree[2]['f']=4.

trie树中每个节点的左右孩子编号没有特殊限制。

插入(insert)

开始初始节点是root=0；tot表示用了多少个节点。

当我们插入一串字符，例如：yyfissb.

首先我们知道tree[root]['y']值为0，也就是没有连边，现在我们用一个节点,tot++,tree[root]['y']=tot=1;

插入以后，这是一个连续的单词，我们就不能再从根节点向外连边了，现在root = tree[root]['y'] = 1.

那么再插入下个y值，确认tree[root(1)]['y']值为0，tot++，再次连边tree[root]['y']=tot,root=tree[root]['y']。

直到插入完b为止。

注意：root不能直接等于tot，因为可能已经存在连边，tot值不会改变。

实现代码：

void insert()//插入单词s
{
    len=strlen(s);//单词s的长度
    root=;//根节点编号为0
    for(int i=;i<len;i++)
    {
        int id=s[i]-'a';//第二种编号
        if(!trie[root][id])//如果之前没有从root到id的前缀
                    trie[root][id]=++tot;//插入，tot即为第一种编号
        root=trie[root][id];//顺着字典树往下走
    }
}

查询(search)

1.查询单词字符前缀

和插入的写法差不多。

插入时我们一个一个的按单词顺序在树中不断找边，若有连边直接线下==向下找，没有连边就建边。

同样查询时，有连边是不断向下深入，而发现没有连边了，那么表明这个单词前缀没有出现过。

拿查询字符串dfzk来说:

开始root=0, tree[root]['d']=7 ,root=tree[root]['d'].

root=7, tree[root]['f']=8,root=tree[root]['f'].

root=8,tree[root]['z']=9,root=tree[root]['z'].

root=9,tree[root]['z']=0，未查询到，表明不存在前缀为‘dfzk’的字符串。

bool find()
{
    len=strlen(s);
    root=;//从根结点开始找
    for(int i=;s[i];i++)
    {
        int x=s[i]-'a';//
        if(trie[root][x]==)   return false;//以root为头结点的x字母不存在，返回0
        root=trie[root][x];//为查询下个字母做准备，往下走
    }
    return true;//找到了
}

2.查询单词是否出现过以。

我们可以再定义一个bool型数组，在每个新单词插入时，最后在结尾节点处进行标记，表明有单词在此处结尾，查询时当这一串字符不能查询到最后一定不存在，查询到最后是判断节点处是否有标记。

3.查询单词或前缀出现的次数

若要查询单词出现的次数，上边的bool型可以直接改为int，结尾处每次++。

查询前缀出现的次数，路径上所有经过的节点每次都++。

int search()
{
    root=;
    len=strlen(s);
    for(int i=;i<len;i++)
    {
        int id=s[i]-'a';
        if(!trie[root][id]) return ;
        root=trie[root][id];
    }//root经过此循环后变成前缀最后一个字母所在位置的后一个位置
    return sum[root];//因为前缀后移了一个保存，所以此时的sum[root]就是要求的前缀出现的次数
}

查询是否出现过代码

/*
  trie tree的储存方式：将字母储存在边上，边的节点连接与它相连的字母
  trie[rt][x]=tot:rt是上个节点编号，x是字母，tot是下个节点编号
*/
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#define maxn 2000010
using namespace std;
int tot=,n;
int trie[maxn][];
//bool isw[maxn];查询整个单词用
void insert(char *s,int rt)
{
    for(int i=;s[i];i++)
    {
        int x=s[i]-'a';
        if(trie[rt][x]==)//现在插入的字母在之前同一节点处未出现过
        {
            trie[rt][x]=++tot;//字母插入一个新的位置，否则不做处理
        }
        rt=trie[rt][x];//为下个字母的插入做准备
    }
    /*isw[rt]=true;标志该单词末位字母的尾结点，在查询整个单词时用到*/
}
bool find(char *s,int rt)
{
    for(int i=;s[i];i++)
    {
        int x=s[i]-'a';
        if(trie[rt][x]==)return false;//以rt为头结点的x字母不存在，返回0
        rt=trie[rt][x];//为查询下个字母做准备
    }
    return true;
    //查询整个单词时，应该return isw[rt]
}
char s[];
int main()
{
    tot=;
    int rt=;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        cin>>s;
        insert(s,rt);
    }
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        cin>>s;
        if(find(s,rt))printf("YES\n");
        else printf("NO\n");
    }
    return ;
}

查询前缀出现的次数代码

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
int trie[][],len,root,tot,sum[];
bool p;
int n,m;
char s[];
void insert()
{
    len=strlen(s);
    root=;
    for(int i=;i<len;i++)
    {
        int id=s[i]-'a';
        if(!trie[root][id]) trie[root][id]=++tot;
        sum[trie[root][id]]++;//前缀后移一个位置保存
        root=trie[root][id];
    }
}
int search()
{
    root=;
    len=strlen(s);
    for(int i=;i<len;i++)
    {
        int id=s[i]-'a';
        if(!trie[root][id]) return ;
        root=trie[root][id];
    }//root经过此循环后变成前缀最后一个字母所在位置的后一个位置
    return sum[root];//因为前缀后移了一个保存，所以此时的sum[root]就是要求的前缀出现的次数
}
int main()
{
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        cin>>s;
        insert();
    }
    scanf("%d",&m);
    for(int i=;i<=m;i++)
    {
        cin>>s;
        printf("%d\n",search());
    }
}