数据结构与算法之美学习笔记：B+树（第48讲）

一、解决问题的前提是定义清楚问题

通过对一些模糊需求进行假设，来限定要解决问题的范围

根据某个值查找数据，比如 select * from use where id=1234；
根据区间值来查询某些数据比如 select * from use where id > 1234 and id < 2345

性能方面的需求，我们主要考察时间和空间两方面，也就是执行效率和存储空间

执行效率：我么你希望通过索引，查询数据的效率尽可能的高；
存储空间方面：我们希望索引不需要消耗太多的内存空间

二、尝试用学过的数据结构解决这个问题

支持快速查询、插入等操作的动态数据结构，我们已经学过散列表、平衡二叉树、跳表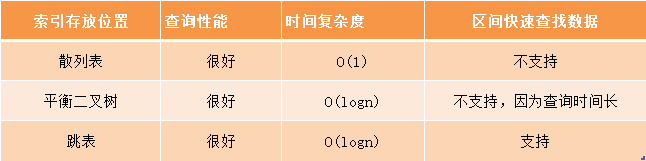

这样看来，跳表是可以解决这个问题，实际上，数据库索引所用到的数据结构跟跳表非常相似，叫做B+树
它是通过跳表演化雇来的，而非跳表

三、改造二叉查找树来解决这个问题

1、实现代码

/**
 * 这是 B+ 树非叶子节点的定义。
 *
 * 假设 keywords=[3, 5, 8, 10]
 * 4 个键值将数据分为 5 个区间：(-INF,3), [3,5), [5,8), [8,10), [10,INF)
 * 5 个区间分别对应：children[0]...children[4]
 *
 * m 值是事先计算得到的，计算的依据是让所有信息的大小正好等于页的大小：
 * PAGE_SIZE = (m-1)*4[keywordss 大小]+m*8[children 大小]
 */
public class BPlusTreeNode {
  public static int m = 5; // 5 叉树
  public int[] keywords = new int[m-1]; // 键值，用来划分数据区间
  public BPlusTreeNode[] children = new BPlusTreeNode[m];// 保存子节点指针
}
 
/**
 * 这是 B+ 树中叶子节点的定义。
 *
 * B+ 树中的叶子节点跟内部结点是不一样的,
 * 叶子节点存储的是值，而非区间。
 * 这个定义里，每个叶子节点存储 3 个数据行的键值及地址信息。
 *
 * k 值是事先计算得到的，计算的依据是让所有信息的大小正好等于页的大小：
 * PAGE_SIZE = k*4[keyw.. 大小]+k*8[dataAd.. 大小]+8[prev 大小]+8[next 大小]
 */
public class BPlusTreeLeafNode {
  public static int k = 3;
  public int[] keywords = new int[k]; // 数据的键值
  public long[] dataAddress = new long[k]; // 数据地址
 
  public BPlusTreeLeafNode prev; // 这个结点在链表中的前驱结点
  public BPlusTreeLeafNode next; // 这个结点在链表中的后继结点
}

2、实现步骤

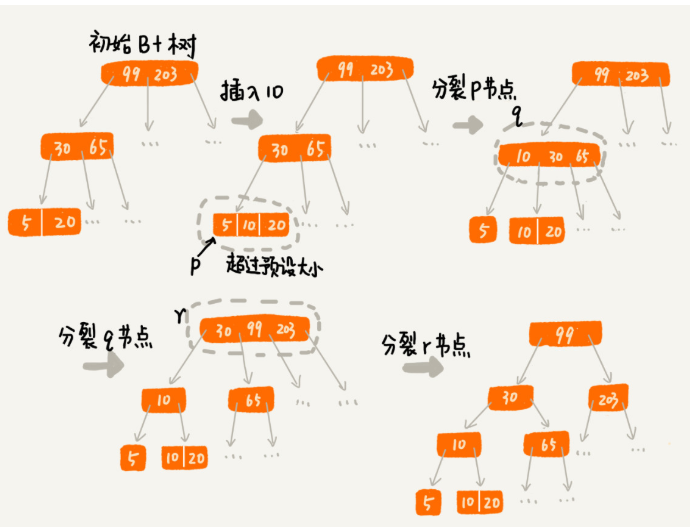
3、实现思路

分裂合并

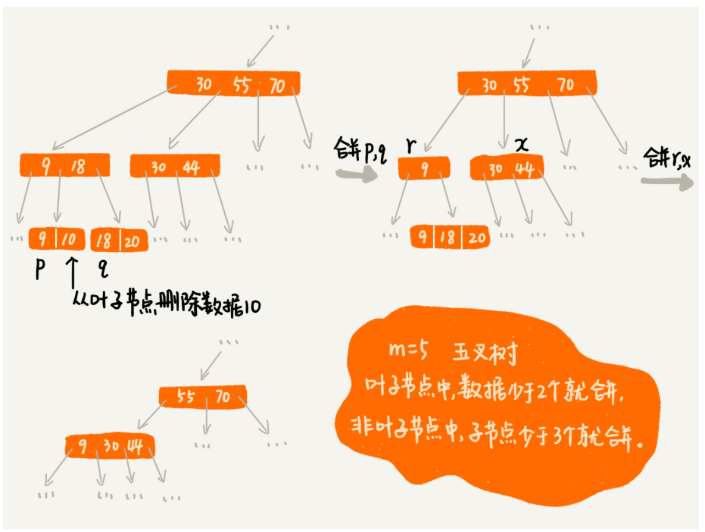
4、删除操作的例子

四、总结引申

1、每个节点中子节点的个数不能超过m，也不能小于m/2
2、根节点的子节点个数不可超过m/2，这是一个例外
3、M叉树只存储索引，并不真正存储数据，这个有点类似跳表
4、通过链表将叶子阶段串联在一次，这样可以方便区间查询
5、一般情况下，根节点会被存储在内存中，其他节点存储在磁盘中