Python全栈-magedu-2018-笔记10

第三章 - Python 内置数据结构

集set

• 约定
  • set 翻译为集合
  • collection 翻译为集合类型，是一个大概念
• set
  • 可变的、无序的、不重复的元素的集合

set定义 初始化

• set() -> new empty set object
• set(iterable) -> new set object

  s1 = set()
  s2 = set(range(5))
  s3 = set(list(range(10)))
  s4 = {} # dict
  s5 = {9,10,11} # set
  s6 = {(1,2),3,'a'}
  s7 = {[1],(1,),1} # unhashable type: 'list'

set的元素

• set的元素要求必须可以hash（因为set就是哈希表啊）
• 目前学过的不可hash的类型有list、set
• 元素不可以索引，因为无序
• set可以迭代

set增加

• add(elem)
  • 增加一个元素到set中
  • 如果元素存在，什么都不做
• update(*others)
  • 合并其他元素到set集合中来
  • 参数others必须是可迭代对象
  • 就地修改

set删除

• remove(elem)
  • 从set中移除一个元素
  • 元素不存在，抛出KeyError异常。为什么是KeyError？
• discard(elem)
  • 从set中移除一个元素
  • 元素不存在，什么都不做
• pop() -> item
  • 移除并返回任意的元素。为什么是任意元素？
  • 空集返回KeyError异常
  • clear()
  • 移除所有元素

set修改、查询

• 修改
  • 要么删除，要么加入新的元素
  • 为什么没有修改？
• 查询
  • 非线性结构，无法索引
• 遍历
  • 可以迭代所有元素
• 成员运算符
  • in 和 not in 判断元素是否在set中
  • 效率呢？与索引访问列表的效率是差不多的，O(1)

set成员运算符的比较

• list和set的比较
• lst1 = list(range(100))
• lst2 = list(range(1000000))
• -1 in lst1、-1 in lst2 看看效率
• set1 = set(range(100))
• set2 = set(range(1000000))
• -1 in set1、-1 in set2 看看效率

set成员运算符的比较

%%timeit lst1=list(range(100))
a = -1 in lst1

%%timeit lst1=list(range(1000000))
a = -1 in lst1

%%timeit set1=set(range(100))
a = -1 in set1

%%timeit set1=set(range(1000000))
a = -1 in set1

set不管元素怎么增加遍历的效率都是一样的。

set和线性结构

• 线性结构的查询时间复杂度是O(n)，即随着数据规模的增大而增加耗时

• set、dict等结构，内部使用hash值作为key，时间复杂度可以做到O(1)，查询时间和数据规模无关

• 可hash
  • 数值型int、float、complex
  • 布尔型True、False
  • 字符串string、bytes
  • tuple
  • None
  • 以上都是不可变类型，成为可哈希类型，hashable

• set的元素必须是可hash的

集合

• 基本概念
  • 全集
    • 所有元素的集合。例如实数集，所有实数组成的集合就是全集
  • 子集subset和超集superset
    • 一个集合A所有元素都在另一个集合B内，A是B的子集，B是A的超集
  • 真子集和真超集
    • A是B的子集，且A不等于B，A就是B的真子集，B是A的真超集
  • 并集：多个集合合并的结果
  • 交集：多个集合的公共部分
  • 差集：集合中除去和其他集合公共部分

集合运算

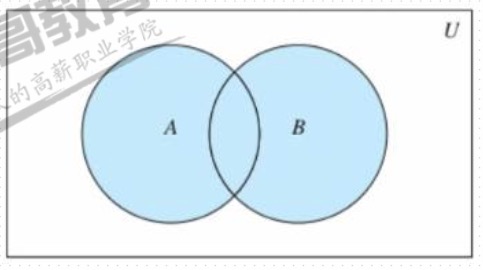
• 并集
  • 将两个集合A和B的所有的元素合并到一起，组成的集合称作集合A与集合B的并集
  • union(*others)
    • 返回和多个集合合并后的新的集合
  • | 运算符重载
    • 等同union
  • update(*others)
    • 和多个集合合并，就地修改
  • |=
    • 等同update

集合运算

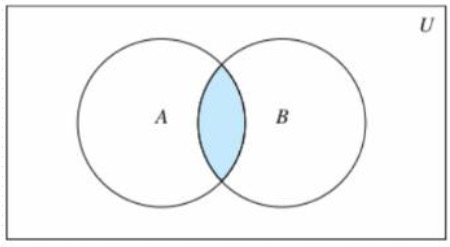
• 交集
  • 集合A和B，由所有属于A且属于B的元素组成的集合
  • intersection(*others)
    • 返回和多个集合的交集
  • &
    • 等同intersection
  • intersection_update(*others)
    • 获取和多个集合的交集，并就地修改
  • &=
    • 等同intersection_update

集合运算

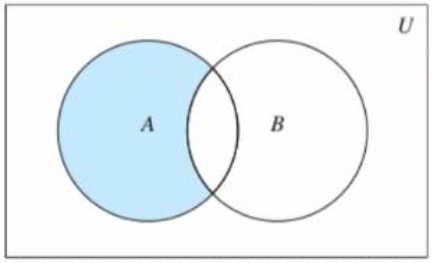
• 差集
  • 集合A和B，由所有属于A且不属于B的元素组成的集合
  • difference(*others)
    • 返回和多个集合的差集
• -
  • 等同difference
• difference_update(*others)
  • 获取和多个集合的差集并就地修改
• -=
  • 等同difference_update

集合运算

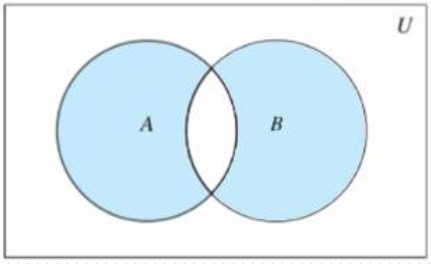
• 对称差集
  • 集合A和B，由所有不属于A和B的交集元素组成的集合，记作（A-B）∪（B-A）
  • symmetric_differece(other)
    • 返回和另一个集合的差集
  • ^
    • 等同symmetric_differece
  • symmetric_differece_update(other)
    • 获取和另一个集合的差集并就地修改
  • ^=
    • 等同symmetric_differece_update

集合运算

• issubset(other)、<=
  • 判断当前集合是否是另一个集合的子集
• set1 < set2
  • 判断set1是否是set2的真子集
• issuperset(other)、>=
  • 判断当前集合是否是other的超集
• set1 > set2
  • 判断set1是否是set的真超集
• isdisjoint(other)
  • 当前集合和另一个集合没有交集
  • 没有交集，返回True

集合应用

• 共同好友
  • 你的好友A、B、C，他的好友C、B、D，求共同好友
    如果是推荐好友，用差集求，不用查库，在内存中集合运算是非常快的，而且往往用到Redis的
• 微信群提醒
  • XXX与群里其他人都不是微信朋友关系
• 权限判断
  • 有一个API，要求权限同时具备A、B、C才能访问，用户权限是B、C、D，判断用户是否能够访问该API
  • 有一个API，要求权限具备A、B、C任意一项就可访问，用户权限是B、C、D，判断用户是否能够访问该API
• 一个总任务列表，存储所有任务。一个完成的任务列表。找出为未完成的任务

解决的方法都不是唯一的，下面仅供参考。

集合应用

• 共同好友
  • 你的好友A、B、C，他的好友C、B、D，求共同好友
  • 交集问题：{'A', 'B', 'C'}.intersection({'B', 'C', 'D'})
• 微信群提醒
  • XXX与群里其他人都不是微信朋友关系
  • 并集：userid in (A | B | C | ...) == False，A、B、C等是微信好友的并集，用户ID不在这个并集中，说明他和任何人都不是朋友

集合应用

• 权限判断
  • 有一个API，要求权限同时具备A、B、C才能访问，用户权限是B、C、D，判断用户是否能够访问该API
    • API集合A，权限集合P
    • A - P = {} ，A-P为空集，说明P包含A
    • A.issubset(P) 也行，A是P的子集也行
    • A & P = A 也行
  • 有一个API，要求权限具备A、B、C任意一项就可访问，用户权限是B、C、D，判断用户是否能够访问该API
    • API集合A，权限集合P
    • A & P != {} 就可以
    • A.isdisjoint(P) == False 表示有交集

集合应用

• 一个总任务列表，存储所有任务。一个已完成的任务列表。找出为未完成的任务
  • 业务中，任务ID一般不可以重复
  • 所有任务ID放到一个set中，假设为ALL
  • 所有已完成的任务ID放到一个set中，假设为COMPLETED，它是ALL的子集
  • ALL - COMPLETED = UNCOMPLETED

集合练习

• 随机产生2组各10个数字的列表，如下要求：
  • 每个数字取值范围[10,20]
  • 统计20个数字中，一共有多少个不同的数字？
  • 2组中，不重复的数字有几个？分别是什么？
  • 2组中，重复的数字有几个？分别是什么？

集合练习

• 随机产生2组各10个数字的列表，如下要求：
  • 每个数字取值范围[10,20]
  • 统计20个数字中，一共有多少个不同的数字？
  • 2组比较，不重复的数字有几个？分别是什么？
  • 2组比较，重复的数字有几个？分别是什么？

  a = [1, 9, 7, 5, 6, 7, 8, 8, 2, 6]
  b = [1, 9, 0, 5, 6, 4, 8, 3, 2, 3]
  s1 = set(a)
  s2 = set(b)
  print(s1)
  print(s2)
  print(s1.union(s2))
  print(s1.symmetric_difference(s2))
  print(s1.intersection(s2))

最后

本文的另外链接是：https://herodanny.github.io/python-magedu-2018-notes10.html