[jzoj]2938.【NOIP2012模拟8.9】分割田地

Link

　　https://jzoj.net/senior/#main/show/2938

Description

　　地主某君有一块由2×n个栅格组成的土地，有k个儿子，现在地主快要终老了，要把这些土地分给这些儿子。分给每个儿子的土地最小的单位是一个栅格，同时，分给同一个儿子的土地要求要相邻连续的。地主觉得分给某个儿子的土地面积至少有一个栅格，但是具体多少可以随意。

　　请问，聪明的你，能够算出地主一共有多少种分土地的方法吗？也就是说要求把2*n的栅格分成k个连通区域，每个区域至少有一个栅格。

Solution

10~90分

　　应该都是正解某些细节没有处理好，或者可以打个递归暴力做一下，可以得到少量的分数

100分

　　这道题是道很好的DP题目，准确来说是递推，因为它有许多情况需要讨论。

　　我们设f[i,k,0/1]表示你选到第i列，其中分配给k个儿子，第i列两个栅格分配给不同一个儿子为0，反之，为1。

　　关键是很难想到转移。

　　其中有9种情况，其实应该有12种情况，因为有的，状态一样，但是情况不一样。

　　[1]、f[i,k,0]:=f[i,k,0]+f[i-1,k-2.0]

　　[2]、f[i,k,0]:=f[i,k,0]+f[i-1,k-2,1]

　　[3]、f[i,k,0]:=f[i,k,0]+f[i-1,k-1,1]*2

　　[4]、f[i,k,0]:=f[i,k,0]+f[i-1,k-1,0]*2

　　[5]、f[i,k,0]:=f[i,k,0]+f[i-1,k,0]

　　[6]、f[i,k,1]:=f[i,k,1]+f[i−1,k−1,0]

　　[7]、f[i,k,1]:=f[i,k,1]+f[i-1,k-1,1]

　　[8]、f[i,k,1]:=f[i,k,1]+f[i-1,k,0]*2

　　[9]、f[i,k,1]:=f[i,k,1]+f[i-1,k,1]

　　状态怎么来呢？与前一列的状态有关，具体可以分成如下9种。盗用别人的图片

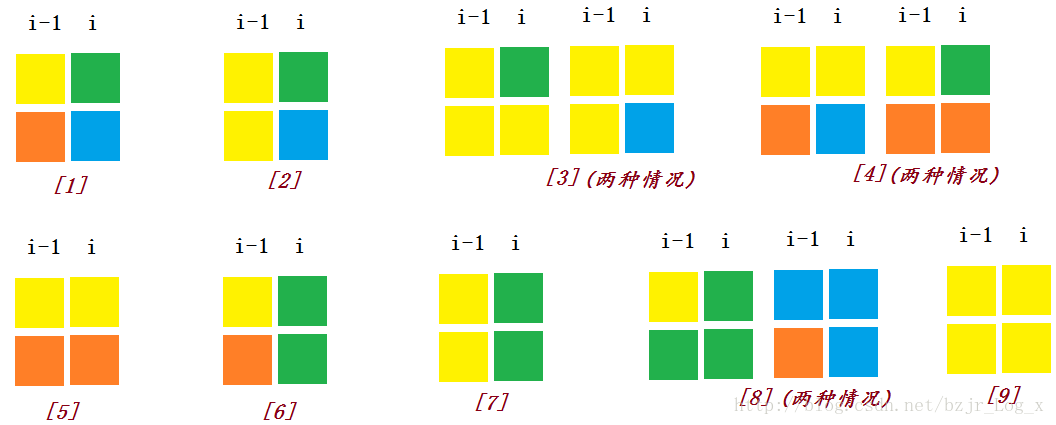
　　自己手推一下，非常容易可以的出来，故本题就迎刃而解了。没有想到递推如此强大。

Code

uses math;
const
        maxn=;
var
        n,m,i,k:longint;
        f:array[..,-..,..] of int64;
begin
        readln(n,m);

        f[,,]:=;
        f[,,]:=;

        for i:= to n do
                for k:= to min(i*,m) do
                begin
                        f[i,k,]:=(f[i,k,]+f[i-,k-,]+f[i-,k-,]+f[i-,k-,]*+f[i-,k-,]*+f[i-,k,]) mod maxn;
                        f[i,k,]:=(f[i,k,]+f[i-,k-,]+f[i-,k-,]+f[i-,k,]*+f[i-,k,]) mod maxn;
                end;

        writeln((f[n,m,]+f[n,m,]) mod maxn);

        writeln(chr());
end.