文本主题模型之潜在语义索引(LSI)

　　　　在文本挖掘中，主题模型是比较特殊的一块，它的思想不同于我们常用的机器学习算法，因此这里我们需要专门来总结文本主题模型的算法。本文关注于潜在语义索引算法(LSI)的原理。

1. 文本主题模型的问题特点

　　　　在数据分析中，我们经常会进行非监督学习的聚类算法，它可以对我们的特征数据进行非监督的聚类。而主题模型也是非监督的算法，目的是得到文本按照主题的概率分布。从这个方面来说，主题模型和普通的聚类算法非常的类似。但是两者其实还是有区别的。

　　　　聚类算法关注于从样本特征的相似度方面将数据聚类。比如通过数据样本之间的欧式距离，曼哈顿距离的大小聚类等。而主题模型，顾名思义，就是对文字中隐含主题的一种建模方法。比如从“人民的名义”和“达康书记”这两个词我们很容易发现对应的文本有很大的主题相关度，但是如果通过词特征来聚类的话则很难找出，因为聚类方法不能考虑到到隐含的主题这一块。

　　　　那么如何找到隐含的主题呢？这个一个大问题。常用的方法一般都是基于统计学的生成方法。即假设以一定的概率选择了一个主题，然后以一定的概率选择当前主题的词。最后这些词组成了我们当前的文本。所有词的统计概率分布可以从语料库获得，具体如何以“一定的概率选择”，这就是各种具体的主题模型算法的任务了。

　　　　当然还有一些不是基于统计的方法，比如我们下面讲到的LSI。

2. 潜在语义索引(LSI)概述

　　　　潜在语义索引(Latent Semantic Indexing,以下简称LSI)，有的文章也叫Latent Semantic  Analysis（LSA）。其实是一个东西，后面我们统称LSI，它是一种简单实用的主题模型。LSI是基于奇异值分解（SVD）的方法来得到文本的主题的。而SVD及其应用我们在前面的文章也多次讲到，比如：奇异值分解(SVD)原理与在降维中的应用和矩阵分解在协同过滤推荐算法中的应用。如果大家对SVD还不熟悉，建议复习奇异值分解(SVD)原理与在降维中的应用后再读下面的内容。

　　　　这里我们简要回顾下SVD：对于一个$m \times n$的矩阵$A$，可以分解为下面三个矩阵：

$$A_{m \times n} = U_{m \times m}\Sigma_{m \times n} V^T_{n \times n}$$

　　　　有时为了降低矩阵的维度到k，SVD的分解可以近似的写为：

$$A_{m \times n} \approx U_{m \times k}\Sigma_{k \times k} V^T_{k \times n}$$

　　　　如果把上式用到我们的主题模型，则SVD可以这样解释：我们输入的有m个文本，每个文本有n个词。而$A_{ij}$则对应第i个文本的第j个词的特征值，这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数，一般要比文本数少。SVD分解后，$U_{il}$对应第i个文本和第l个主题的相关度。$V_{jm}$对应第j个词和第m个词义的相关度。$\Sigma_{lm}$对应第l个主题和第m个词义的相关度。

　　　　也可以反过来解释：我们输入的有m个词，对应n个文本。而$A_{ij}$则对应第i个词档的第j个文本的特征值，这里最常用的是基于预处理后的标准化TF-IDF值。k是我们假设的主题数，一般要比文本数少。SVD分解后，$U_{il}$对应第i个词和第l个词义的相关度。$V_{jm}$对应第j个文本和第m个主题的相关度。$\Sigma_{lm}$对应第l个词义和第m个主题的相关度。

　　　　这样我们通过一次SVD，就可以得到文档和主题的相关度，词和词义的相关度以及词义和主题的相关度。

3. LSI简单实例

　　　　这里举一个简单的LSI实例，假设我们有下面这个有11个词三个文本的词频TF对应矩阵如下：

　　　　

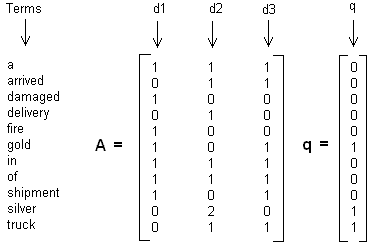
　　　　这里我们没有使用预处理，也没有使用TF-IDF，在实际应用中最好使用预处理后的TF-IDF值矩阵作为输入。

　　　　我们假定对应的主题数为2，则通过SVD降维后得到的三矩阵为：

　　　　从矩阵$U_k$我们可以看到词和词义之间的相关性。而从$V_k$可以看到3个文本和两个主题的相关性。大家可以看到里面有负数，所以这样得到的相关度比较难解释。

4. LSI用于文本相似度计算

　　　　在上面我们通过LSI得到的文本主题矩阵可以用于文本相似度计算。而计算方法一般是通过余弦相似度。比如对于上面的三文档两主题的例子。我们可以计算第一个文本和第二个文本的余弦相似度如下 ：$$sim(d1,d2) = \frac{(-0.4945)*(-0.6458) + (0.6492)*(-0.7194)}{\sqrt{(-0.4945)^2+0.6492^2}\sqrt{(-0.6458)^2+(-0.7194)^2}}$$

5. LSI主题模型总结

　　　　LSI是最早出现的主题模型了，它的算法原理很简单，一次奇异值分解就可以得到主题模型，同时解决词义的问题，非常漂亮。但是LSI有很多不足，导致它在当前实际的主题模型中已基本不再使用。

　　　　主要的问题有：

　　　　1） SVD计算非常的耗时，尤其是我们的文本处理，词和文本数都是非常大的，对于这样的高维度矩阵做奇异值分解是非常难的。

　　　　2） 主题值的选取对结果的影响非常大，很难选择合适的k值。

　　　　3） LSI得到的不是一个概率模型，缺乏统计基础，结果难以直观的解释。

　　　　对于问题1），主题模型非负矩阵分解（NMF）可以解决矩阵分解的速度问题。对于问题2），这是老大难了，大部分主题模型的主题的个数选取一般都是凭经验的，较新的层次狄利克雷过程（HDP）可以自动选择主题个数。对于问题3），牛人们整出了pLSI(也叫pLSA)和隐含狄利克雷分布(LDA)这类基于概率分布的主题模型来替代基于矩阵分解的主题模型。

　　　　回到LSI本身，对于一些规模较小的问题，如果想快速粗粒度的找出一些主题分布的关系，则LSI是比较好的一个选择，其他时候，如果你需要使用主题模型，推荐使用LDA和HDP。

（欢迎转载，转载请注明出处。欢迎沟通交流： liujianping-ok@163.com）