AVL树和平衡二叉树 平衡因子 右旋转LL 左旋转RR LR RL

　　前言

　　今天要介绍几种高级数据结构AVL树，介绍之前AVL，会先说明平衡二叉树，并将树的学习路线进行总结，并介绍维持平衡的方法：右旋转、左旋转。

　　一、树学习路线

　　1、路线总结

　　总结了一下树的学习路线，如下图：

　　

　　2、说明

　　上面这个图要从上往下进行一步一步学习；首先，从二叉树开始学习，要对树的一些概念有一些基本了解，如树的左孩子和右孩子等，然后对树的遍历方法：先序、中序和后序遍历都熟练掌握，有精力再把层序遍历掌握；

　　接下来，大部分的树，都是在二叉树的基础上加了许多特性而形成的，所以二叉树是基础，如二叉搜索树，任意一个节点都比左子树大，都比右子树小，主要用于解决查找问题，对二分查找法有一个基本了解，还有一个特性，二分搜索树的中序遍历：数据就从从小到大进行排序了。

　　AVL树，是今天要讲的话题，下面会详细进行讲解。

　　红黑树应该是大名鼎鼎了，都应该听过了，之后我会专门介绍。

　　trie树就不再是二叉树了，是多叉树了，之后也会讲解。

　　二、平衡二叉树

　　1、定义

　　平衡二叉树，首先是二叉树，并且对于任意一个节点，左子树和右子树的高度差不能超过1。

　　2、意义

　　有了二分查找树为什么还要平衡二叉树呢？这篇对二分查找树进行了详细介绍,并对先序、中序和后序进行了明确说明，可以参考：https://www.cnblogs.com/liudw-0215/p/9835691.html，因为二叉树有一个弊端就是会退化为链表，就是只有左子树或右子树有节点，这样查询效率就会变低了。所以，就需要“平衡”这个概念了。

　　3、平衡因子

　　先画个图，进行说明，不是平衡二叉树，只是为了说明问题，如下图：

　　

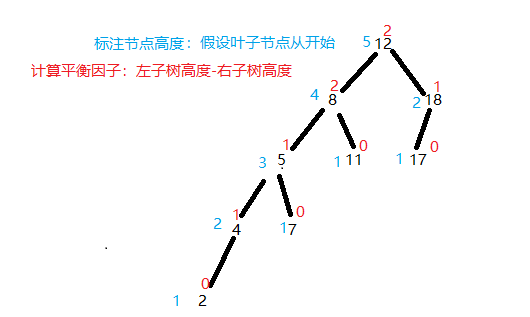
　　说明：如上图，树的高度从叶子节点开始，并且叶子节点高度是1；平衡因子就是用左子树高度减去右子树高度，例如：4这个节点，左子树2的高度为1，右子树没有则为0，所以4这个节点的平衡因子为1。

　　三、AVL树

　　1、定义

　　　　AVL树是自平衡二分搜索树，既具有平衡性和二分性。

　　　2、构建AVL树类

　　　　是在二分搜索树的基础上进行修改并维持“平衡”这个特性的，首先，来看下AVL树的类，如下：

#ifndef AVLTREE_AVLTREE_H
#define AVLTREE_AVLTREE_H

#include <algorithm>
#include <iostream>
#include <vector>

template<typename Key, typename Value>
class AVLTree {
private:
    struct Node {
        Key key;
        Value value;
        Node *left;
        Node *right;
        int height;    //用于标注高度，计算平衡因子

        Node(Key key, Value value) {
            this->key = key;
            this->value = value;
            this->left = this->right = nullptr;
            height = ;
        }

        Node(Node *node) {
            this->key = node->key;
            this->value = node->value;
            this->left = node->left;
            this->right = node->right;
            this->height = node->height;
        }
    };

    Node *root;
    int size;

public:

    AVLTree() {
        root = nullptr;
        size = ;
    }

    ~AVLTree() {
        destroy(root);
    }

    int getSize() {
        return size;
    }

    int isEmpty() {
        return size == ;
    }

    int getHeight(Node *node) {    //获取高度
        if (node == nullptr) {
            return ;
        }
        return node->height;
    }

    int getBalanceFactor(Node *node) {    //获取平衡因子
        if (node == nullptr) {
            return ;
        }
        return getHeight(node->left) - getHeight(node->right);
    }

    bool isBST() {
        std::vector<Key> keys;
        inOrder(root, keys);
        for (int i = ; i < keys.size(); ++i) {
            if (keys.at(i - ) < keys.at(i)) {
                return false;
            }
        }
        return true;
    }

    bool isBalanced() {
        return isBalanced(root);
    }

    void add(Key key, Value value) {
        root = add(root, key, value);
    }

    bool contains(Key key) {
        return getNode(root, key) != nullptr;
    }

    Value *get(Key key) {
        Node *node = getNode(root, key);
        return node == nullptr ? nullptr : &(node->value);
    }

    void set(Key key, Value newValue) {
        Node *node = getNode(root, key);
        if (node != nullptr) {
            node->value = newValue;
        }
    }

    // 从二叉树中删除键值为key的节点
    Value *remove(Key key) {
        Node *node = getNode(root, key);
        if (node != nullptr) {
            root = remove(root, key);
            return &(node->value);
        }
        return nullptr;
    }

private:

    // 向以node为根的二叉搜索树中,插入节点(key, value)
    // 返回插入新节点后的二叉搜索树的根
    Node *add(Node *node, Key key, Value value) {
        if (node == nullptr) {
            size++;
            return new Node(key, value);
        }
        if (key == node->key) {
            node->value = value;
        } else if (key < node->key) {
            node->left = add(node->left, key, value);
        } else {
            node->right = add(node->right, key, value);
        }
        node->height =  + std::max(getHeight(node->left), getHeight(node->right));
        int balanceFactor = getBalanceFactor(node);
        if (std::abs(balanceFactor) > ) {
            std::cout << "unbalanced : " << balanceFactor;
        }
        return node;
    }

    // 在以node为根的二叉搜索树中查找key所对应的Node
    Node *getNode(Node *node, Key key) {
        if (node == nullptr) {
            return nullptr;
        }
        if (key == node->key) {
            return node;
        } else if (key < node->key) {
            return getNode(node->left, key);
        } else {
            return getNode(node->right, key);
        }
    }

    void destroy(Node *node) {
        if (node != nullptr) {
            destroy(node->left);
            destroy(node->right);
            delete node;
            size--;
        }
    }

    // 在以node为根的二叉搜索树中,返回最小键值的节点
    Node *minimum(Node *node) {
        if (node->left == nullptr)
            return node;
        return minimum(node->left);
    }

    // 在以node为根的二叉搜索树中,返回最大键值的节点
    Node *maximum(Node *node) {
        if (node->right == nullptr)
            return node;
        return maximum(node->right);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    Node *removeMin(Node *node) {
        if (node->left == nullptr) {
            Node *rightNode = node->right;
            delete node;
            size--;
            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    Node *removeMax(Node *node) {
        if (node->right == nullptr) {
            Node *leftNode = node->left;
            delete node;
            size--;
            return leftNode;
        }

        node->right = removeMax(node->right);
        return node;
    }

    // 删除掉以node为根的二分搜索树中键值为key的节点
    // 返回删除节点后新的二分搜索树的根
    Node *remove(Node *node, Key key) {
        if (node == nullptr) {
            return nullptr;
        }
        if (key < node->key) {
            node->left = remove(node->left, key);
            return node;
        } else if (key > node->key) {
            node->right = remove(node->right, key);
            return node;
        } else {
            if (node->left == nullptr) {
                Node *rightNode = node->right;
                delete node;
                size--;
                return rightNode;
            }

            if (node->right == nullptr) {
                Node *leftNode = node->left;
                delete node;
                size--;
                return leftNode;
            }

            Node *successor = new Node(minimum(node->right));
            //Node *precursor = new Node(maximum(node->right));
            size++;

            successor->right = removeMin(node->right);
            successor->left = node->left;
            //precursor->left = removeMax(node->left);
            //precursor->right = node->right;

            delete node;
            size--;

            return successor;
            //return precursor;
        }
    }

    void inOrder(Node *node, std::vector<Key> keys) {
        if (node == nullptr) {
            return;
        }
        inOrder(node->left, keys);
        keys.push_back(node->key);
        inOrder(node->right, keys);
    }

    bool isBalanced(Node *node) {
        if (node == nullptr) {
            return true;
        }

        int balanceFactor = getBalanceFactor(node);
        if (std::abs(balanceFactor) > ) {
            return false;
        }

        return isBalanced(node->left) && isBalanced(node->right);
    }
};

#endif //AVLTREE_AVLTREE_H

　　增加height属性，用于记录每个节点的高度，并计算平衡因子；

　　3、获取节点高度

　　把height属性返回就可以了：

int getHeight(Node *node) {    //获取高度
        if (node == nullptr) {
            return ;
        }
        return node->height;
    }

　　4、获取平衡因子

　　将左子树高度减去右子树高度即可，但注意：不要区绝对值，因为之后的旋转要判断左子树还是右子树的高度高，代码如下：

　　

int getBalanceFactor(Node *node) {    //获取平衡因子
        if (node == nullptr) {
            return ;
        }
        return getHeight(node->left) - getHeight(node->right);
    }

　　5、判断是不是平衡二叉树

　　平衡因子大于1就不是平衡二叉树了，代码如下：

　　

bool isBalanced(Node *node) {
        if (node == nullptr) {
            return true;
        }

        int balanceFactor = getBalanceFactor(node);
        if (std::abs(balanceFactor) > ) {
            return false;
        }

        return isBalanced(node->left) && isBalanced(node->right);
    }

bool isBalanced() {
        return isBalanced(root);
    }

　　四、AVL树的旋转

　　　1、什么时维护平衡？

　　如下图，假如原来没有2这个节点，那么树是平衡二叉树，但插入2之后，就不再平衡了，这时就需要维护平衡了，大体上有4种情况需要维护平衡，来说明这一种。

　　　　

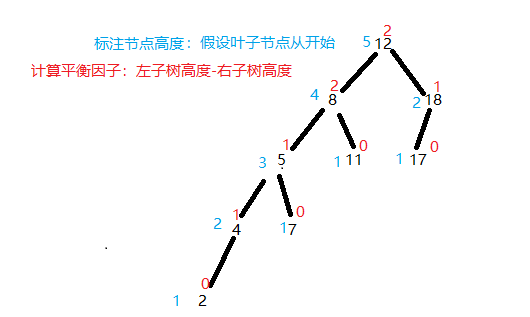
　　　　2、右旋转　LL

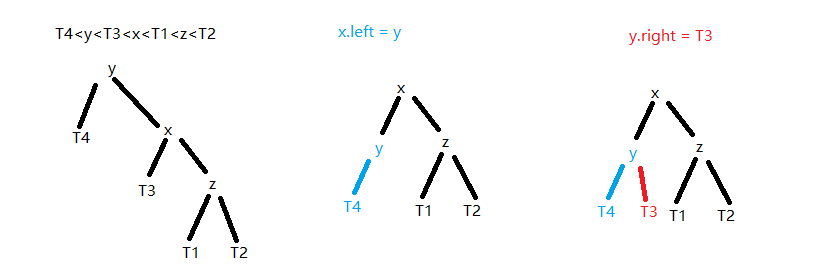
　　　　将其中的部分节点抽离出来，如下图：

　　

　　说明：主要分为两步：

　　第一步：将T3保存，然后将y以及孩子节点旋转到x的右孩子位置，相对于x，y是顺时针向右旋转的，所以叫右旋转；

　　第二步：将T3移到y的左孩子位置

　　最后，形成的二叉树符合二分和平衡两个性质，所以还是平衡二叉树。

　　3、右旋转代码实现

　　上图应该已经讲解的很明白了吧，代码如下：

　　

Node *rightRotate(Node *y) {
        Node *x = y->left;    //存x
        Node *tmp = x->right;    //将x的右孩子备份
        x->right = y;    //将y右旋转到x的右孩子
        y->left = tmp;    //将x的右孩子移到y的左侧
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + ;    //修改y高度，注意要先修改y的高度
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + ;    //修改x的高度
        return x;
    }

　　4、左旋转 RR

　　左旋转和右旋转很相似，只是方向不同，如下图：

　　

　　说明：相对于x，y是逆时针向左旋转，所以是左旋转

　　5、左旋转代码实现

　　左旋转代码跟右旋转很相似，代码如下：

　　

Node *leftRotate(Node *y){
        Node *x = y->right;
        Node *tmp = x->left;
        x->left = y;
        y->right = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + ;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + ;
        return x;
    }

　　6、LR

　　还有两种情况需要讨论，LL代表“左左”，LR代表“左右”，如下图：

　　

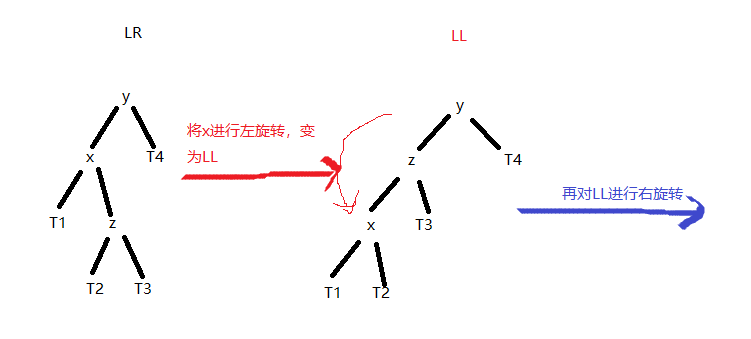
　　说明：借助左旋转将LR转为LL，再对LL进行右旋转就OK了，所以理解左、右旋转是基础！

　　7、LR代码实现

　　代码如下：

　　

if (balanceFactor >  && getBalanceFactor(node->left) < ) {    //LR
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }

　　8、RL

　　最后一种情况RL，如下图：

　　

　　9、RL代码实现

　　代码如下：

　　

if (balanceFactor < - && getBalanceFactor(node->right) > ) {    //RL
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }

　　总结

　　AVL树和平衡二叉树就比较难了，主要理解右旋转和左旋转，对之后理解红黑树有巨大作用！