scikit-learn 决策树 分类问题

1.Demo

from sklearn import tree
import pydotplus
import numpy as np
#李航p59表数据
#年龄，有工作，有自己房子，信贷情况，类别
#青年0    中年1     老年2
#否0     是1
#一般0    好1      非常好2
datasets = np.array([['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', ''],
               ['', '', '', '', '']])
X = datasets[:,:4]
Y = datasets[:,4:5]
clf = tree.DecisionTreeClassifier()
clf.fit(X,Y)
dot_data = tree.export_graphviz(clf,out_file=None)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf("Tree.pdf")

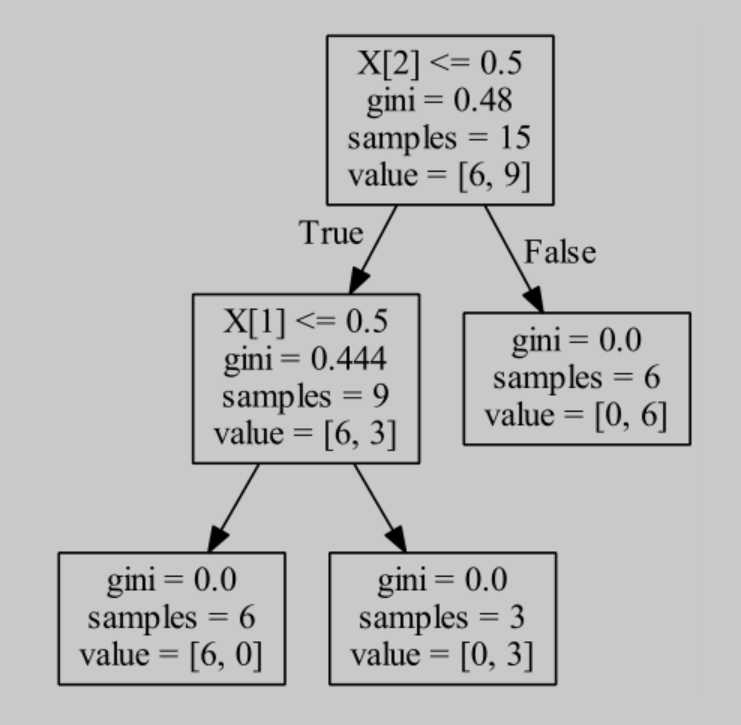
 生成的可视化的决策树

2.DecisionTreeClassifier

class sklearn.tree.DecisionTreeClassifier(criterion=’gini’, splitter=’best’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, class_weight=None, presort=False)

重要参数

criterion : string, optional (default=”gini”)

用来指定特征选择的方法，有"entropy"和"gini"两个选择

entropy指定用信息增益，使用ID3、C4.5算法

gini指定用基尼不纯度，使用CART决策树算法

splitter : string, optional (default=”best”)

用来指定怎么寻找最优划分点，有"best"和"random"两个选择

best指定在所有特征中找最优划分点

random指定在随机部分划分中找最优划分点

默认的"best"适合样本量不大的时候，而如果样本数据量非常大，此时决策树构建推荐"random"

max_depth : int or None, optional (default=None)

用来指定决策树的最大深度

通常将max_depth=3作为初始值，将数据可视化查看下拟合情况，在调整树的深度

通常用来解决过拟合问题

min_samples_split : int, float, optional (default=2)

用来指定子树划分条件

默认是2，当只有一个样本的时候，不在划分子树

当样本数很大时，才会考虑增加这个值

限制决策树增长，避免过拟合

min_samples_leaf : int, float, optional (default=1)

用来指定叶子节点包含的最少样本

当样本数很大时，才会考虑增加这个值

限制决策树增长，避免过拟合