TensorFlow机器学习实战指南之第二章
一、计算图中的操作
在这个例子中,我们将结合前面所学的知识,传入一个列表到计算图中的操作,并打印返回值:
声明张量和占位符。这里,创建一个numpy数组,传入计算图操作:
import tensorflow as tf
import numpy as np # Create graph
sess = tf.Session()
# Create data to feed in
x_vals = np.array([1., 3., 5., 7., 9.])
x_data = tf.placeholder(tf.float32)
m = tf.constant(3.)
# Multiplication
prod = tf.multiply(x_data, m)
for x_val in x_vals:
print(sess.run(prod, feed_dict={x_data: x_val}))
输出:
3.0
9.0
15.0
21.0
27.0
在下面这个例子中,我们将学习如何在同一个计算图中进行多个乘法操作。
下面我们将用两个矩阵乘以占位符,然后做加法。传入两个矩阵(三维numpy数组):
我们将传入两个形状为3×5的numpy数组,然后
每个矩阵乘以常量矩阵(形状为:5×1),将返回一个形状为3×1的矩阵。紧接着再乘以1×1的矩阵,返回的
结果矩阵仍然为3×1。最后,加上一个3×1的矩阵,示例如下:
1.首先,创建数据和占位符:
# Create graph
sess = tf.Session()
# Create data to feed in
my_array = np.array([[1., 3., 5., 7., 9.],
[-2., 0., 2., 4., 6.],
[-6., -3., 0., 3., 6.]])
x_vals = np.array([my_array, my_array + 1])
x_data = tf.placeholder(tf.float32, shape=(3, 5))
2.接着,创建矩阵乘法和加法中要用到的常量矩阵:
m1 = tf.constant([[1.],[0.],[-1.],[2.],[4.]])
m2 = tf.constant([[2.]])
a1 = tf.constant([[10.]])
3.现在声明操作,表示成计算图:
# 1st Operation Layer = Multiplication
prod1 = tf.matmul(x_data, m1) # 2nd Operation Layer = Multiplication
prod2 = tf.matmul(prod1, m2) # 3rd Operation Layer = Addition
add1 = tf.add(prod2, a1)
4.最后,通过计算图赋值:
for x_val in x_vals:
print(sess.run(add1, feed_dict={x_data: x_val}))
输出:
[[102.]
[ 66.]
[ 58.]]
[[114.]
[ 78.]
[ 70.]]
在我们通过计算图运行数据之前心里要有个数:声明数据形状,预估操作返回值形状。由于预先不知道
或者维度在变化,情况也可能发生变化。为了实现目标,我们指明变化的维度,或者事先不知道的维度设为
none。例如,占位符有未知列维度,使用方式如下:
x_data = tf.placeholder(tf.float32,shape=(3,None))
二、TensorFlow的多层Layer
1.首先,通过numpy创建2D图像,4×4像素图片。我们将创建成四维:第一维和最后一维大小为1。注
意,TensorFlow的图像函数是处理四维图片的,这四维是:图片数量、高度、宽度和颜色通道。这里是一张
图片,单颜色通道,所以设两个维度值为1:
# Create graph
sess = tf.Session() # Create a small random 'image' of size 4x4
x_shape = [1, 4, 4, 1]
x_val = np.random.uniform(size=x_shape)
2.下面在计算图中创建占位符。此例中占位符是用来传入图片的,代码如下:
x_data = tf.placeholder(tf.float32, shape=x_shape)
3.为了创建过滤4×4像素图片的滑动窗口,我们将用TensorFlow内建函数conv2d()(常用来做图像处
理)卷积2×2形状的常量窗口。conv2d()函数传入滑动窗口、过滤器和步长。本例将在滑动窗口四个方向
上计算,所以在四个方向上都要指定步长。创建一个2×2的窗口,每个方向长度为2的步长。为了计算平均
值,我们将用常量为0.25的向量与2×2的窗口卷积,代码如下:
my_filter = tf.constant(0.25, shape=[2, 2, 1, 1])
my_strides = [1, 2, 2, 1]
mov_avg_layer = tf.nn.conv2d(x_data, my_filter, my_strides,
padding='SAME', name='Moving_Avg_Window')
4.注意,我们通过conv2d()函数的name参数,把这层Layer命名为“Moving_Avg_Window”。
5.现在定义一个自定义Layer,操作滑动窗口平均的2×2的返回值。自定义函数将输入张量乘以一个2×2
的矩阵张量,然后每个元素加1。因为矩阵乘法只计算二维矩阵,所以剪裁图像的多余维度(大小为1)。
TensorFlow通过内建函数squeeze()剪裁。下面是新定义的Layer:
def custom_layer(input_matrix):
input_matrix_sqeezed = tf.squeeze(input_matrix)
A = tf.constant([[1., 2.], [-1., 3.]])
b = tf.constant(1., shape=[2, 2])
temp1 = tf.matmul(A, input_matrix_sqeezed)
temp = tf.add(temp1, b) # Ax + b
return(tf.sigmoid(temp))
6.现在把刚刚新定义的Layer加入到计算图中,并且用tf.name_scope()命名唯一的Layer名字,后续在
计算图中可折叠/扩展Custom_Layer层,代码如下:
# Add custom layer to graph
with tf.name_scope('Custom_Layer') as scope:
custom_layer1 = custom_layer(mov_avg_layer)
7.为占位符传入4×4像素图片,然后执行计算图,代码如下:
print(sess.run(custom_layer1, feed_dict={x_data: x_val}))
输出:
[[0.9027293 0.9333066 ]
[0.84296674 0.8839635 ]]
三、TensorFlow实现损失函数
损失函数(loss function)对机器学习来讲是非常重要的。它们度量模型输出值与目标值(target)间的
差值。本节会介绍TensorFlow中实现的各种损失函数。
为了优化机器学习算法,我们需要评估机器学习模型训练输出结果。在TensorFlow中评估输出结果依赖
损失函数。损失函数告诉TensorFlow,预测结果相比期望的结果是好是坏。在大部分场景下,我们会有算法
模型训练的样本数据集和目标值。损失函数比较预测值与目标值,并给出两者之间的数值化的差值。
为了比较不同损失函数的区别,我们将会在图表中绘制出来。先创建计算图,然后加载
matplotlib(Python的绘图库),代码如下:
import matplotlib.pyplot as plt
import tensorflow as tf
首先,将讲解回归算法的损失函数。回归算法是预测连续因变量的。创建预测序列和目标序列作为张
量,预测序列是-1到1之间的等差数列,代码如下:
# Numerical Predictions
x_vals = tf.linspace(-1., 1., 500)
target = tf.constant(0.)
1.回归模型的损失函数
(1)L2正则损失函数(即欧拉损失函数)。L2正则损失函数是预测值与目标值差值的平方和。注意,上述
例子中目标值为0。L2正则损失函数是非常有用的损失函数,因为它在目标值附近有更好的曲度,机器学习
算法利用这点收敛,并且离目标越近收敛越慢,代码如下:
# L2 loss
# L = (pred - actual)^2
l2_y_vals = tf.square(target - x_vals)
l2_y_out = sess.run(l2_y_vals)
注意:
TensorFlow有内建的L2正则形式,称为nn.l2_loss()。这个函数其实是实际L2正则
的一半,换句话说,它是上面l2_y_vals的1/2。
(2)L1正则损失函数(即绝对值损失函数)。与L2正则损失函数对差值求平方不同的是,L1正则损失函数
对差值求绝对值。L1正则在目标值附近不平滑,这会导致算法不能很好地收敛。代码如下:
# L1 loss
# L = abs(pred - actual)
l1_y_vals = tf.abs(target - x_vals)
l1_y_out = sess.run(l1_y_vals)
(3)Pseudo-Huber 损失函数
Pseudo-Huber损失函数是Huber损失函数的连续、平滑估计,试图利用L1和L2正则削减极值处的陡峭,
使得目标值附近连续。它的表达式依赖参数delta。我们将绘图来显示delta1=0.25和delta2=5的区别
Huber损失函数经常用于回归问题,它是分段函数,公式如下:
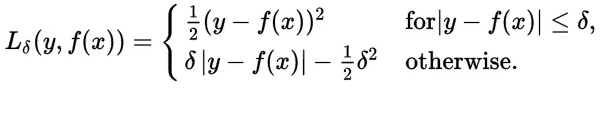
从这个公式可以看出当残差(预测值与目标值的差值,即y-f(x) )很小的时候,损失函数为L2范数,残差大的时候,为L1范数的线性函数。
Peseudo-Huber损失函数是Huber损失函数的连续、平滑估计,在目标附近连续,公式如下:
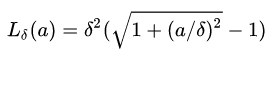
该公式依赖于参数delta,delta越大,则两边的线性部分越陡峭。
# Pseudo-Huber loss
# L = delta^2 * (sqrt(1 + ((pred - actual)/delta)^2) - 1)
delta1 = tf.constant(0.25)
phuber1_y_vals = tf.multiply(tf.square(delta1), tf.sqrt(1. + tf.square((target - x_vals) / delta1)) - 1.)
phuber1_y_out = sess.run(phuber1_y_vals) delta2 = tf.constant(5.)
phuber2_y_vals = tf.mul(tf.square(delta2), tf.sqrt(1. + tf.square((target - x_vals) / delta2)) - 1.)
phuber2_y_out = sess.run(phuber2_y_vals)
以下为L1、L2、Huber损失函数的对比图如下,其中Huber的delta取0.25、5两个值:

x_array = sess.run(x_vals)
plt.plot(x_array, l2_y_out, 'b-', label='L2 Loss')
plt.plot(x_array, l1_y_out, 'r--', label='L1 Loss')
plt.plot(x_array, phuber1_y_out, 'k-.', label='P-Huber Loss(0.25)')
plt.plot(x_array, phuber2_y_out, 'g:', label='P-Huber Loss(5.)')
plt.ylim(-0.2, 0.4)
plt.legend(loc='lower right', prop={'size': 11})
plt.show()
2.分类模型的损失函数
分类损失函数主要用于评估预测分类结果,重新定义预测值(-3至5的等差序列)和目标值(目标值为1),如下:
y_pred=tf.linspace(-3., 5., 100) y_target=tf.constant(1.) y_targets=tf.fill([100, ], 1.)
(1)Hinge损失函数
Hinge损失常用于二分类问题,主要用来评估向量机算法,但有时也用来评估神经网络算法,公式如下:
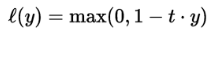
loss_hinge_vals = tf.maximum(0., 1. – tf.mul(y_target, y_pred)) loss_hinge_out = sess.run(loss_hinge_vals)
(2)两类交叉熵(Cross-entropy)损失函数
交叉熵来自于信息论,是分类问题中使用广泛的损失函数。交叉熵刻画了两个概率分布之间的距离,当两个概率分布越接近时,它们的交叉熵也就越小,给定两个概率分布p和q,则距离如下:
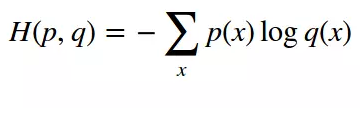
对于两类问题,当一个概率p=y,则另一个概率q=1-y,因此代入化简后的公式如下:
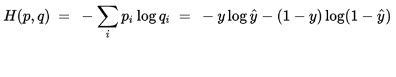
# Cross entropy loss
# L = -actual * (log(pred)) - (1-actual)(log(1-pred))
xentropy_y_vals = - tf.multiply(target, tf.log(x_vals)) - tf.multiply((1. - target), tf.log(1. - x_vals))
xentropy_y_out = sess.run(xentropy_y_vals)
(3)Sigmoid交叉熵损失函数
与上面的两类交叉熵类似,只是将预测值y_pred值通过sigmoid函数进行转换,再计算交叉熵损失。
# Sigmoid entropy loss
# L = -actual * (log(sigmoid(pred))) - (1-actual)(log(1-sigmoid(pred)))
# or
# L = max(actual, 0) - actual * pred + log(1 + exp(-abs(actual)))
xentropy_sigmoid_y_vals = tf.nn.sigmoid_cross_entropy_with_logits(labels=x_vals, logits=targets)
xentropy_sigmoid_y_out = sess.run(xentropy_sigmoid_y_vals)
(4)加权交叉熵损失函数
加权交叉熵损失函数是Sigmoid交叉熵损失函数的加权,是对正目标的加权。假定权重为0.5,在TensorFlow中的调用方式如下:
# Weighted (softmax) cross entropy loss
# L = -actual * (log(pred)) * weights - (1-actual)(log(1-pred))
# or
# L = (1 - pred) * actual + (1 + (weights - 1) * pred) * log(1 + exp(-actual))
weight = tf.constant(0.5)
xentropy_weighted_y_vals = tf.nn.weighted_cross_entropy_with_logits(x_vals, targets, weight)
xentropy_weighted_y_out = sess.run(xentropy_weighted_y_vals)
(5)Softmax交叉熵损失函数
Softmax交叉熵损失函数是作用于非归一化的输出结果,只针对单个目标分类计算损失。
通过softmax函数将输出结果转化成概率分布,从而便于输入到交叉熵里面进行计算(交叉熵要求输入为概率),softmax定义如下:
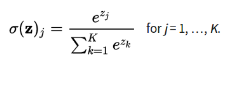
结合前面的交叉熵定义公式,则Softmax交叉熵损失函数公式如下:
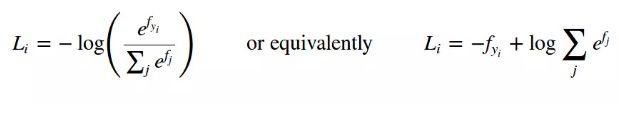
# Softmax entropy loss
# L = -actual * (log(softmax(pred))) - (1-actual)(log(1-softmax(pred)))
unscaled_logits = tf.constant([[1., -3., 10.]])
target_dist = tf.constant([[0.1, 0.02, 0.88]])
softmax_xentropy = tf.nn.softmax_cross_entropy_with_logits_v2(labels=unscaled_logits, logits=target_dist)
用于回归相关的损失函数,对比图如下:

3.总结
下面对各种损失函数进行一个总结,如下表所示:

在实际使用中,对于回归问题经常会使用MSE均方误差(L2取平均)计算损失,对于分类问题经常会使用Sigmoid交叉熵损失函数。
TensorFlow机器学习实战指南之第二章的更多相关文章
- TensorFlow机器学习实战指南之第二章2
TensorFlow实现反向传播 本节先举个简单的回归算法的例子.这里先举一个简单的例子,从均值1,标准差为0.1的正态分布中随机抽样100个数,然后乘以变量A,损失函数L2正则函数,也就是实现函数X ...
- TensorFlow机器学习实战指南之第一章
TensorFlow基础 一.TensorFlow算法的一般流程 1.导入/生成样本数据集 2.转换和归一化数据:一般来讲,输入样本数据集并不符合TensorFlow期望的形状,所以需要转换数据格式以 ...
- 学习TF:《TensorFlow机器学习实战指南》中文PDF+英文PDF+代码
从实战角度系统讲解TensorFlow基本概念及各种应用实践.真实的应用场景和数据,丰富的代码实例,详尽的操作步骤,带你由浅入深系统掌握TensorFlow机器学习算法及其实现. <Tensor ...
- HTTP权威指南:第二章
URL概览 前面提到,URL资源是HTTP协议所使用的寻找资源位置的定位符.分为三个部分,主要的结构是: 方案://服务器/路径 这种结构使得网络上的每一个资源都只有唯一的命名方法,从而使得浏览器可以 ...
- Spring 3.x 实践 第一个例子(Spring 3.x 企业应用开发实战读书笔记第二章)
前言:工作之后一直在搞android,现在需要更多和后台的人员交涉,技术栈不一样,难免鸡同鸭讲,所以稍稍学习下. 这个例子取自于<Spring 3.x 企业应用开发实战>一书中的第二章,I ...
- 《SDN核心技术剖析和实战指南》第一章小结
第一章主要是概况.新技术有一个特点是,每家都有不同的说法.这里我只说说我比较认同的部分. SDN的核心概念大概有两个:转发面与控制面分离.开发可编程化.书里还说逻辑上集中控制,其实这个就可以从转发与控 ...
- PMP备考指南之第二章:项目运作环境
本文已同步至 GitHub/Gitee/公众号,感兴趣的同学帮忙点波关注~ 第二章:项目运作环境 1. 事业环境因素.组织过程资产 事业环境因素 Enterprise Environmental Fa ...
- Windows Forms编程实战学习:第二章 欢迎使用Visual Studio
第二章 欢迎使用Visual Studio 1,AssemblyInfo文件 包含程序集的属性,向应用程序添加元数据 [assembly:<attribute>(<setting&g ...
- java并发编程实战笔记---(第二章)线程安全:正确性
ThreadA__________ 同步 ______________ 异步 ___________ 异步 ThreadB__________ ____________ ...
随机推荐
- git 命令提交项目到github
git 命令提交项目到github步骤如下: 1.使用git 命令客户端进入项目根路径,输入 git init 命令,创建github本地根目录 2.把文件加入到本地项目 git add . ,如 ...
- vue将网页中的特定部分转成pdf并下载(仅供个人学习记录)
先安装支持 将页面html转换成图片npm install --save html2canvas 将图片生成pdfnpm install jspdf --save 组件引用: import html2 ...
- python基础知识总结(二)
基础数据类型初始: int(数字):+ 加 - 减 * 乘 / 除 % 取余数 str(字符串):python中凡是用引号引起来的都是字符串 可以相加,用来表示字符串的拼接 可以相乘,只能 ...
- IP通信基础课堂笔记----关于数链层
课前回顾 IOS从上到下分别有:应用层,传输层,网络层,数链层,物理层. IP是网络层的地址,MAC是数链层的地址,IP必须通过ARP才能转换成MAC地址. 课堂内容 1.如何在数链层实现发送端数据无 ...
- makefile笔记7 - makefile函数
在 Makefile 中可以使用函数来处理变量,从而让我们的命令或是规则更为的灵活和具有智能. make 所支持的函数也不算很多,不过已经足够我们的操作了.函数调用后,函数的返回值可以当做变量来使用. ...
- makefile笔记2 - makefile总述
一.makefile的组成 Makefile 里主要包含了五个东西:显示规则.隐晦规则.变量定义.文件指示和注释. 1. 显示规则.显示规则说明了,如何生成一个或多的的目标文件.这是由 Makefil ...
- Selenium常用API详解介绍
转至元数据结尾 由 黄从建创建, 最后修改于一月 21, 2019 转至元数据起始 一.selenium元素定位 1.selenium定位方法 2.定位方法的用法 二.控制浏览器操作 1.控制 ...
- vgcreate语法
vgcreate 用于创建LVM卷组 补充说明 vgcreate命令 用于创建LVM卷组.卷组(Volume Group)将多个物理卷组织成一个整体,屏蔽了底层物理卷细节.在卷组上创建逻辑卷时不用考虑 ...
- opendaylight-O版本与openstack集成
feature:list list (Lists all existing features available from the defined repositories) feature:list ...
- CSS常用属性-xy
一.文本Text CSS text-align 属性 文本对齐方式 CSS text-decoration 属性 text-decoration 属性规定添加到文本的修饰 CSS line-heigh ...
