[USACO20FEB]Equilateral Triangles P 题解

优雅的暴力。

设三个点为 \((i,j,k)\)，则有 \(6\) 个未知数即 \(x_i,x_j,x_k,y_i,y_j,y_k\)。又因为有 \(2\) 条关于这 \(6\) 个未知数的方程 \(ij=jk,ij=ik\)，所以一定能通过枚举其中的 \(4\) 个量来求解，时间复杂度 \(O(n^4)\)。

而这个 \(O(n^4)\) 的暴力是肉眼可见的跑不满（

---

考虑先枚举点 \(i\)，则有以下四种情况：

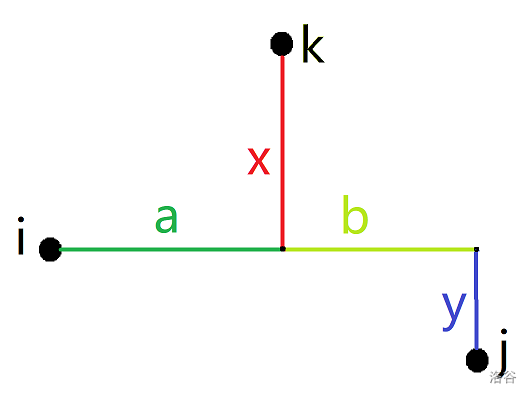
解得 \(x=a,y=a-b\)。

其中，\(a,x>0,0\le b,y \le a\)。

解得 \(x=a,y=a-b\)。

其中，其中，\(a,x>0,0\le b,y\le a,\color{red}b\not= 0\)。

解得 \(x=2b-a,y=b-a\)。

其中，\(0\le a<b,0\le x,y\)。

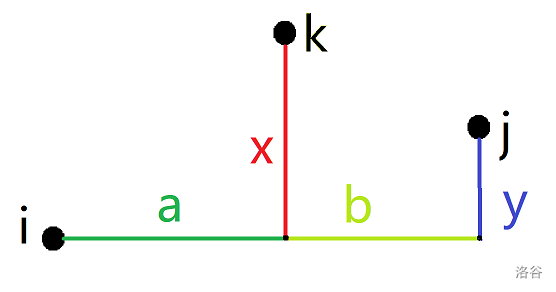
解得 \(x=2b-a,y=b-a\)。

其中，\(0\le a<b,0\le x,y,\color{red}a\not=0\)。

---

注意，有些同时存在于两种情况的状态， 需要通过标红的判断去除。

然后就能敲出以下代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn=310;
inline int read(){
	int x=0;
	char c=getchar();
	for(;(c^'.')&&(c^'*');c=getchar());
	return c=='*';
}
bool c[maxn][maxn];
int n,ans;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			c[i][j]=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			if(!c[i][j]) continue;
			for(int a=0;a<=n;a++){
				for(int b=0;b<=a;b++){
					if(a&&i+a<=n&&j+a<=n&&i-a+b>0&&j+a+b<=n)
						ans+=(c[i+a][j+a]&c[i-a+b][j+a+b]);
					if(a&&b&&i-a>0&&j+a<=n&&i+a-b<=n&&j+a+b<=n)
						ans+=(c[i-a][j+a]&c[i+a-b][j+a+b]);
				}
				for(int b=a+1;b<=n;b++){
					if(i-b-b+a>0&&j+a<=n&&i-b+a>0&&j+a+b<=n)
						ans+=(c[i-b-b+a][j+a]&c[i-b+a][j+a+b]);
					if(a&&i+b+b-a<=n&&j+a<=n&&i+b-a<=n&&j+a+b<=n)
						ans+=(c[i+b+b-a][j+a]&c[i+b-a][j+a+b]);
				}
			}
		}
	printf("%d\n",ans);
	return 0;
}

然后你会获得 \(51pt\) 的高分。

容易发现，代码中搜索到了许多冗余的状态，考虑将判断放到循环之外：

#include<bits/stdc++.h>
using namespace std;
const int maxn=310;
inline int read(){
	int x=0;
	char c=getchar();
	for(;(c^'.')&&(c^'*');c=getchar());
	return c=='*';
}
bool c[maxn][maxn];
int n,ans;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			c[i][j]=read();
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++){
			if(!c[i][j]) continue;
			for(int a=0;a<=n;a++){
				if(a&&i+a<=n&&j+a<=n)
					for(int b=max(a-i+1,0);b<=a&&j+a+b<=n;b++)
						ans+=(c[i+a][j+a]&c[i-a+b][j+a+b]);
				if(a&&i-a>0&&j+a<=n)
					for(int b=max(i+a-n,1);b<=a&&b<=n-j-a;b++)
						ans+=(c[i-a][j+a]&c[i+a-b][j+a+b]);
				if(j+a<=n)
					for(int b=a+1;j+a+b<=n&&b+b<i+a;b++)
						ans+=(c[i-b-b+a][j+a]&c[i-b+a][j+a+b]);
				if(a&&j+a<=n)
					for(int b=a+1;j+a+b<=n&&b+b<=n-i+a;b++)
						ans+=(c[i+b+b-a][j+a]&c[i+b-a][j+a+b]);
			}
		}
	printf("%d\n",ans);
	return 0;
}

然后就过了。

祝AC。