instance1：

求解下列线性规划问题

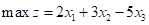
s.t.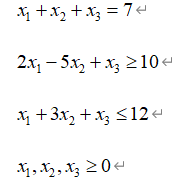  

代码：

from scipy import optimize
import numpy as np
c = np.array([2,3,-5])
A = np.array([[-2,5,-1],[1,3,1]])
B = np.array([-10,12])
#要与A对应，是二维矩阵
Aeq = np.array([[1,1,1]])
Beq = np.array([7])
#linprog解决的是最小问题，因此要加上-号
res = optimize.linprog(-c,A,B,Aeq,Beq)
print(res)

基于python的数学建模---scipy库的更多相关文章

  1. Python数模笔记-Scipy库（1）线性规划问题

    1.最优化问题建模 最优化问题的三要素是决策变量.目标函数和约束条件. (1)分析影响结果的因素是什么,确定决策变量 (2)决策变量与优化目标的关系是什么,确定目标函数 (3)决策变量所受的限制条件是 ...

  2. scapy - 基于python的数据包操作库

    简介 地址:https://github.com/secdev/scapy scapy是一个基于python的交互式数据包操作程序和库. 它能够伪造或者解码多种协议的数据包,通过使用pcap文件对他们 ...

  3. 使用Python scipy linprog 线性规划求最大值或最小值(使用Python学习数学建模笔记)

    函数格式 scipy.optimize.linprog(c, A_ub=None, b_ub=None, A_eq=None, b_eq=None, bounds=None, method='simp ...

  4. 基于Python的开源人脸识别库：离线识别率高达99.38%

    项目地址:https://github.com/ageitgey/face_recognition#face-recognition 本文的模型使用了C++工具箱dlib基于深度学习的最新人脸识别方法 ...

  5. 使用wxpy这个基于python实现的微信工具库的一些常见问题

    使用如下的命令行安装: pip install wxpy Collecting wxpy Downloading https://files.pythonhosted.org/packages/6b/ ...

  6. Python数学建模-01.新手必读

    Python 完全可以满足数学建模的需要. Python 是数学建模的最佳选择之一,而且在其它工作中也无所不能. 『Python 数学建模 @ Youcans』带你从数模小白成为国赛达人. 1. 数学 ...

  7. python常用框架及第三方库

    python常用框架及第三方库 一.Web框架 1.Django: 开源web开发框架,它鼓励快速开发,并遵循MVC设计,比较庞大,开发周期短.Django的文档最完善.市场占有率最高.招聘职位最多. ...

  8. Python图形界面开发—wxPython库的布局管理及页面切换

    前言 wxPython是基于Python的跨平台GUI扩展库,对wxWidgets( C++ 编写)封装实现.GUI程序的开发中界面布局是很重要的一个部分,合理的页面布局能够给予用户良好使用体验.虽然 ...

  9. Python小白的数学建模课-09 微分方程模型

    小白往往听到微分方程就觉得害怕,其实数学建模中的微分方程模型不仅没那么复杂,而且很容易写出高水平的数模论文. 本文介绍微分方程模型的建模与求解,通过常微分方程.常微分方程组.高阶常微分方程 3个案例手 ...

  10. Python小白的数学建模课-B5. 新冠疫情 SEIR模型

    传染病的数学模型是数学建模中的典型问题,常见的传染病模型有 SI.SIR.SIRS.SEIR 模型. 考虑存在易感者.暴露者.患病者和康复者四类人群,适用于具有潜伏期.治愈后获得终身免疫的传染病. 本 ...

随机推荐

  1. 【读书笔记】C#高级编程 第二章 核心C#

    (一)第一个C#程序 创建一个控制台应用程序,然后输入代码,输入完毕后点击F5 Console.WriteLine();这条语句的意思:把括号内的内容输出到界面上: Console.ReadKey() ...

  2. [Python]-os模块-文件读取

    import os 在Python中,os模块用来处理文件路径,比较方便. os读取文件 在读取文件过程中,最常用的几个功能如下: os.listdir() 获取此目录下的所有目录名,并且存为列表.在 ...

  3. 【ProxySQL】ProxySQL Cluster的搭建

    文章转载自:https://blog.51cto.com/l0vesql/2104643 背景 早期的ProxySQL若需要做高可用,需要搭建两个实例,进行冗余.但两个ProxySQL实例之间的数据并 ...

  4. tcp_tw_recycle参数引发的故障

    文章转载自:https://blog.csdn.net/wireless_tech/article/details/6405755 故障描述: 2010年9月7日,新上线的手机游戏论坛有部分地区用户反 ...

  5. 在K8S中安装jenkins

    以 NFS 为存储卷的示例,将在 NFS 存储卷上创建 Jenkins 目录,然后创建 NFS 类型的 PV.PVC. 1.NFS 存储卷创建 Jenkins 目录 进入 NFS Server 服务器 ...

  6. Handler机制与生产者消费者模式

    本文梳理了 Handler 的源码,并详细阐述了 Handler 与生产者消费者模式的关系,最后给出了多版自定义 Handler 实现.本文首发于简书,重新整理发布. 一.Handler Handle ...

  7. NSIS检测到窗口最小化闪烁提示

    #检测到窗口为最小化时闪烁提示 !include nsDialogs.nsh #编写:水晶石 Name "IsIconic Example" OutFile "IsIco ...

  8. centos7中配置java + mysql +jdk +使用jar部署项目

    centos7中配置java + mysql +jdk  +使用jar部署项目 思维导图 1. 配置JDK環境 1.1下载jdk安装包 Java Downloads | Oracle 1.2 将下载j ...

  9. 洛谷P1884 [USACO12FEB]Overplanting S （矩形切割）

    一种矩形切割的做法: 1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 const in ...

  10. <三>从编译器角度理解C++代码编译和链接原理

    1代码 点击查看代码 **sum.cpp** int gdata=10; int sum(int a,int b){ return a+b; } **main.cpp** extern int gda ...