二分查找-LeetCode704 简单题

LeetCode代码链接：https://leetcode.cn/problems/binary-search/

题目：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例1：

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例2：

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

思路

这道题目的前提是数组为有序数组，同时题目还强调数组中无重复元素，因为一旦有重复元素，使用二分查找法返回的元素下标可能不是唯一的，这些都是使用二分法的前提条件，当大家看到题目描述满足如上条件的时候，可要想一想是不是可以用二分法了。

二分查找涉及的很多的边界条件，逻辑比较简单，但就是写不好。例如到底是 while(left < right) 还是 while(left <= right)，到底是right = middle呢，还是要right = middle - 1呢？

大家写二分法经常写乱，主要是因为对区间的定义没有想清楚，区间的定义就是不变量。要在二分查找的过程中，保持不变量，就是在while寻找中每一次边界的处理都要坚持根据区间的定义来操作，这就是循环不变量规则。

写二分法，区间的定义一般为两种，左闭右闭即[left, right]，或者左闭右开即[left, right)。这里我主要讲解左闭右闭。

左闭右闭写法

区间的定义这就决定了二分法的代码应该如何写，因为定义target在[left, right]区间，所以有如下两点：

• while (left <= right) 要使用 <= ，因为left == right是有意义的，所以使用 <=
• if (nums[middle] > target) right 要赋值为 middle - 1，因为当前这个nums[middle]一定不是target，那么接下来要查找的左区间结束下标位置就是 middle - 1

例如在数组：1,2,3,4,7,9,10中查找元素2，如图所示（参考代码随想录）：

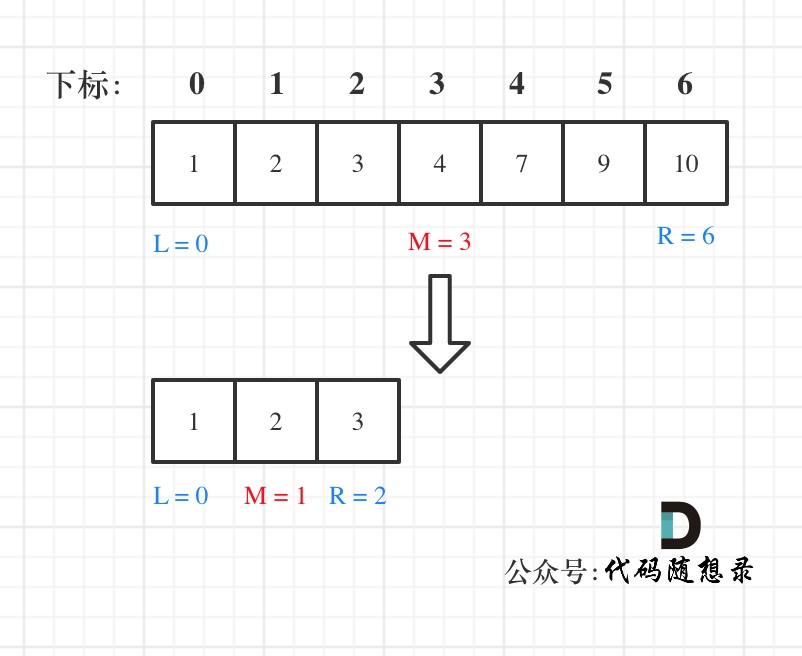
java代码如下：

class Solution {
    public int search(int[] nums, int target) {
        // 避免当 target 小于nums[0] nums[nums.length - 1]时多次循环运算
        if (target < nums[0] || target > nums[nums.length - 1]) {
            return -1;
        }
        int left = 0, right = nums.length - 1;
        while (left <= right) {
            int mid = left + ((right - left) >> 1);
            if (nums[mid] == target)
                return mid;
            else if (nums[mid] < target)
                left = mid + 1;
            else if (nums[mid] > target)
                right = mid - 1;
        }
        return -1;
    }
}

首先先判断数组以及目标值是否满足要求，然后定义左右两边界，while (left <= right)这句话很重要，接着求mid值，这里不使用（left+right）/2而是left + ((right - left) >> 1)是为了防止数过大而出界。最后就是上述思路进行求解，怎么样是不是很简单？

其实二分法的思路大概是这样，只要掌握了思路，遇到类似的题目都不怕。我们下次题再见！！！