视觉十四讲：第七讲_3D-2D：P3P

1.P3P

P3P输入数据为三对3D-2D的匹配点，一个单目相机，经过初始化，得到初始的3D点，就可以依次得到后续的姿态和3D点。



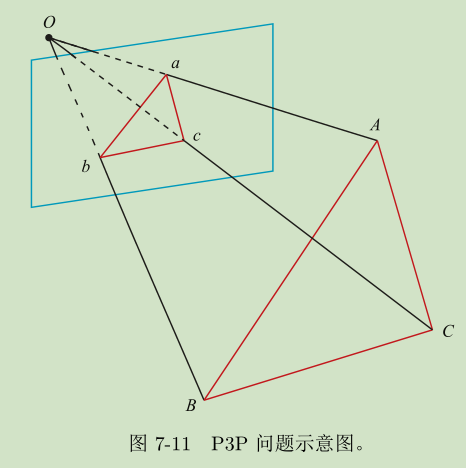
ABC是上一时刻求的的3D点， abc是与上一次时刻的匹配点。利用相似原理，可求出abc在相机坐标下的3D坐标，最后就可以把问题转换为3D-3D坐标的估计问题。

• 问题：只利用3个点，不能运用多余的信息；受噪声影响，存在无匹配，容易算法失败

通常做法是用P3P估计出相机位姿，然后再构建最小二乘优化问题对估计值进行优化调整（Bundle Adjustment）

2.使用Pnp来求解

int main(int argc, char **argv) {
  if (argc != 5) {
    cout << "usage: pose_estimation_3d2d img1 img2 depth1 depth2" << endl;
    return 1;
  }
  //-- 读取图像
  Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);
  assert(img_1.data && img_2.data && "Can not load images!");

  vector<KeyPoint> keypoints_1, keypoints_2;
  vector<DMatch> matches;
  //获取匹配点
  find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
  cout << "一共找到了" << matches.size() << "组匹配点" << endl;

  // 建立3D点
  Mat d1 = imread(argv[3], CV_LOAD_IMAGE_UNCHANGED);       // 第一张图的深度图为16位无符号数，单通道图像
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector<Point3f> pts_3d;
  vector<Point2f> pts_2d;
  for (DMatch m:matches) {
	//取出第一张图匹配点的深度数据
    //Mat.ptr<>(行)[列]
    ushort d = d1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
    if (d == 0)   // bad depth
      continue;
    float dd = d / 5000.0;
	//将图1的匹配点的像素坐标转相机归一化坐标
    Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
	//转换为相机坐标的3D点
    pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));
	//获取图2的匹配点的像素坐标
    pts_2d.push_back(keypoints_2[m.trainIdx].pt);
  }

  cout << "3d-2d pairs: " << pts_3d.size() << endl;

  /**************pnp**************/
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  Mat r, t;
  solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法
  Mat R;
  cv::Rodrigues(r, R); // r为旋转向量形式，用Rodrigues公式转换为矩阵
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve pnp in opencv cost time: " << time_used.count() << " seconds." << endl;

  cout << "R=" << endl << R << endl;
  cout << "t=" << endl << t << endl;
}

3.使用高斯牛顿法来优化求解

1.构建最小二乘问题：

\(T^{*}=argmin\frac{1}{2} \displaystyle \sum^{n}_{i=1}||u_{i}-\frac{1}{s_{i}}KTP_{i}||^{2}_{2}\)

误差是观测像素点-投影像素点，称为重投影误差

使用高斯牛顿法的重点在于求误差项对于每个优化变量的导数

线性化：\(e(x+\Delta x) \approx e(x) + J^{T}\Delta x\)

高斯的增量方程为： \((\displaystyle \sum^{100}_{i=1} J_{i}(\sigma^{2})^{-1} J_{i}^{T})\Delta x_{k}=\displaystyle \sum^{100}_{i=1} -J_{i}(\sigma^{2})^{-1} e_{i}\)

\(H\Delta x_{k}=b\)

2.求雅可比矩阵：

1.使用非齐次坐标，像素误差e是2维，x为相机位姿是6维，\(J^{T}\)是一个2*6的矩阵。

2.将P变换到相机坐标下为\(P^{'}=[X^{'},Y^{'},Z^{'}]^{T}\),则：\(su=KP^{'}\)

3.消去s得：\(u=f_{x}\frac{X^{'}}{Z^{'}}+c_{x}\) \(v=f_{y}\frac{Y^{'}}{Z^{'}}+c_{y}\)

4.对T左乘扰动量\(\delta \xi\),考虑e的变化关于扰动量的导数。则\(\frac{\partial e}{\partial \delta \xi}= \frac{\partial e}{\partial P^{'}} \frac{\partial P^{'}}{\partial \delta \xi}\)

5.容易得出\(\frac{\partial e}{\partial P^{'}}\) = \(-\left[ \begin{matrix} \frac{f_{x}}{Z^{'}} & 0 & -\frac{f_{x}X^{'}}{Z^{'2}} \\ 0 & \frac{f_{y}}{Z^{'}} & -\frac{f_{y}Y^{'}}{Z^{'2}} \end{matrix} \right]\)

6.由李代数导数得：\(\frac{\partial (TP)}{\partial \delta \xi} = \left[ \begin{matrix} I & -P^{' \Lambda} \\ 0^{T} & 0^{T} \end{matrix} \right]\)

7.在\(P^{'}\)的定义中，取了前三维，所以\(\frac{\partial P^{'}}{\partial \delta \xi} = \left[ \begin{matrix} I & -P^{' \Lambda} \end{matrix} \right]\)

8.将两个式子相乘就可以得到雅可比矩阵：

\(\frac{\partial e}{\partial \delta \xi} = - \left[ \begin{matrix} \frac{f_{x}}{Z^{'}} & 0 & -\frac{f_{x}X^{'}}{Z^{'2}} & -\frac{f_{x}X^{'}Y^{'}}{Z^{'2}} & f_{x} + \frac{f_{x}X^{'2}}{Z^{'2}} &- \frac{f_{x}Y^{'}}{Z^{'}} \\ 0 & \frac{f_{y}}{Z^{'}} & -\frac{f_{y}Y^{'}}{Z^{'2}} & -f_{y} - \frac{f_{y}Y^{'2}}{Z^{'2}} & \frac{f_{y}X^{'}Y^{'}}{Z^{'2}} & \frac{f_{y}X^{'}}{Z^{'}} \end{matrix} \right]\)

3.程序：

void bundleAdjustmentGaussNewton(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {
  typedef Eigen::Matrix<double, 6, 1> Vector6d;
  const int iterations = 10;
  double cost = 0, lastCost = 0;
  double fx = K.at<double>(0, 0);
  double fy = K.at<double>(1, 1);
  double cx = K.at<double>(0, 2);
  double cy = K.at<double>(1, 2);

  for (int iter = 0; iter < iterations; iter++) {
    Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
    Vector6d b = Vector6d::Zero();

    cost = 0;
    // compute cost
    for (int i = 0; i < points_3d.size(); i++) {
	  //世界坐标转为相机坐标
      Eigen::Vector3d pc = pose * points_3d[i];
      double inv_z = 1.0 / pc[2];
      double inv_z2 = inv_z * inv_z;
	  //相机坐标转为像素坐标
      Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);

      Eigen::Vector2d e = points_2d[i] - proj;  //误差，观测值-预测值，反之取负

      cost += e.squaredNorm();  //误差里的每项平方和
      Eigen::Matrix<double, 2, 6> J;
	  //雅可比矩阵赋值
      J << -fx * inv_z,
        0,
        fx * pc[0] * inv_z2,
        fx * pc[0] * pc[1] * inv_z2,
        -fx - fx * pc[0] * pc[0] * inv_z2,
        fx * pc[1] * inv_z,
        0,
        -fy * inv_z,
        fy * pc[1] * inv_z2,
        fy + fy * pc[1] * pc[1] * inv_z2,
        -fy * pc[0] * pc[1] * inv_z2,
        -fy * pc[0] * inv_z;

      H += J.transpose() * J;
      b += -J.transpose() * e;
    }

    Vector6d dx;
    dx = H.ldlt().solve(b);

    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }

    if (iter > 0 && cost >= lastCost) {
      // cost increase, update is not good
      cout << "cost: " << cost << ", last cost: " << lastCost << endl;
      break;
    }

    // update your estimation
	//更新位姿
    pose = Sophus::SE3d::exp(dx) * pose;
    lastCost = cost;

    cout << "iteration " << iter << " cost=" << std::setprecision(12) << cost << endl;
  //范数,误差足够小
    if (dx.norm() < 1e-6) {
      // converge
      break;
    }
  }

  cout << "pose by g-n: \n" << pose.matrix() << endl;
}

4.使用g2o来进行BA优化

• 节点(待优化的变量)： 第二个相机的位姿 \(T \in SE(3)\)
• 边(误差)： 每个3D在第二个相机中的投影

1.构建节点和边框架：

// 曲线模型的顶点，模板参数：优化变量维度和数据类型
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  // 初始化
  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();
  }

  //更新估计值
  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}
};

// 误差模型 模板参数：观测值维度，类型，连接顶点类型
class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;
  //输入的变量：位姿，相机内参
  EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}

  //计算误差
  virtual void computeError() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    //获取估计值
    Sophus::SE3d T = v->estimate();
    //将3D世界坐标转为相机像素坐标
    Eigen::Vector3d pos_pixel = _K * (T * _pos3d);
    //归一化
    pos_pixel /= pos_pixel[2];
    //计算误差
    _error = _measurement - pos_pixel.head<2>();
  }

  //计算雅可比矩阵，公式上面已推导
  virtual void linearizeOplus() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    //世界坐标转化为相机坐标
    Eigen::Vector3d pos_cam = T * _pos3d;
    //获取相机内参
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    //传入雅可比矩阵参数
    _jacobianOplusXi
      << -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,
      0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}

private:
  Eigen::Vector3d _pos3d;
  Eigen::Matrix3d _K;
};

2.组成图优化：

void bundleAdjustmentG2O(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {

  // 构建图优化，先设定g2o
  typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;  // 位姿维度为6，误差维度为3
  typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
  // 梯度下降方法，可以从GN, LM, DogLeg 中选
  auto solver = new g2o::OptimizationAlgorithmGaussNewton(
    g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
  g2o::SparseOptimizer optimizer;     // 图模型
  optimizer.setAlgorithm(solver);   // 设置求解器
  optimizer.setVerbose(true);       // 打开调试输出

  // 往图中添加节点
  VertexPose *vertex_pose = new VertexPose(); // camera vertex_pose
  vertex_pose->setId(0);
  vertex_pose->setEstimate(Sophus::SE3d());
  optimizer.addVertex(vertex_pose);

  // K 相机内参
  Eigen::Matrix3d K_eigen;
  K_eigen <<
          K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),
    K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),
    K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);

  // edges 边
  int index = 1;
  for (size_t i = 0; i < points_2d.size(); ++i) {
    auto p2d = points_2d[i];
    auto p3d = points_3d[i];
    EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
    edge->setId(index);
    edge->setVertex(0, vertex_pose); // 设置连接的顶点
    edge->setMeasurement(p2d);  //传入观测值
    edge->setInformation(Eigen::Matrix2d::Identity()); // 信息矩阵
    optimizer.addEdge(edge);
    index++;
  }

  //执行优化
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.setVerbose(true);
  optimizer.initializeOptimization();
  optimizer.optimize(10);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
  //获取结果
  cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;
  pose = vertex_pose->estimate();
}

5.完整代码

#include <iostream>
#include <opencv2/core/core.hpp>
#include <opencv2/features2d/features2d.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/calib3d/calib3d.hpp>
#include <Eigen/Core>
#include <g2o/core/base_vertex.h>
#include <g2o/core/base_unary_edge.h>
#include <g2o/core/sparse_optimizer.h>
#include <g2o/core/block_solver.h>
#include <g2o/core/solver.h>
#include <g2o/core/optimization_algorithm_gauss_newton.h>
#include <g2o/solvers/dense/linear_solver_dense.h>
#include <sophus/se3.hpp>
#include <chrono>

using namespace std;
using namespace cv;

void find_feature_matches(
  const Mat &img_1, const Mat &img_2,
  std::vector<KeyPoint> &keypoints_1,
  std::vector<KeyPoint> &keypoints_2,
  std::vector<DMatch> &matches);

// 像素坐标转相机归一化坐标
Point2d pixel2cam(const Point2d &p, const Mat &K);

// BA by g2o
//STL容器中的元素是Eigen的数据结构，例如这里定义一个vector容器，元素是Vector2d
typedef vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>> VecVector2d;
typedef vector<Eigen::Vector3d, Eigen::aligned_allocator<Eigen::Vector3d>> VecVector3d;

void bundleAdjustmentG2O(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose
);

// BA by gauss-newton
void bundleAdjustmentGaussNewton(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose
);

int main(int argc, char **argv) {
  if (argc != 5) {
    cout << "usage: pose_estimation_3d2d img1 img2 depth1 depth2" << endl;
    return 1;
  }
  //-- 读取图像
  Mat img_1 = imread(argv[1], CV_LOAD_IMAGE_COLOR);
  Mat img_2 = imread(argv[2], CV_LOAD_IMAGE_COLOR);
  assert(img_1.data && img_2.data && "Can not load images!");

  vector<KeyPoint> keypoints_1, keypoints_2;
  vector<DMatch> matches;
  //获取匹配点
  find_feature_matches(img_1, img_2, keypoints_1, keypoints_2, matches);
  cout << "一共找到了" << matches.size() << "组匹配点" << endl;

  // 建立3D点
  Mat d1 = imread(argv[3], CV_LOAD_IMAGE_UNCHANGED);       // 第一张图的深度图为16位无符号数，单通道图像
  Mat K = (Mat_<double>(3, 3) << 520.9, 0, 325.1, 0, 521.0, 249.7, 0, 0, 1);
  vector<Point3f> pts_3d;
  vector<Point2f> pts_2d;
  for (DMatch m:matches) {
	//取出第一张图匹配点的深度数据
    ushort d = d1.ptr<unsigned short>(int(keypoints_1[m.queryIdx].pt.y))[int(keypoints_1[m.queryIdx].pt.x)];
    if (d == 0)   // bad depth
      continue;
    float dd = d / 5000.0;
	//将图1的匹配点的像素坐标转相机归一化坐标
    Point2d p1 = pixel2cam(keypoints_1[m.queryIdx].pt, K);
	//转换为相机坐标的3D点
    pts_3d.push_back(Point3f(p1.x * dd, p1.y * dd, dd));
	//获取图2的匹配点的像素坐标
    pts_2d.push_back(keypoints_2[m.trainIdx].pt);
  }

  cout << "3d-2d pairs: " << pts_3d.size() << endl;

  /**************pnp**************/
  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  Mat r, t;
  solvePnP(pts_3d, pts_2d, K, Mat(), r, t, false); // 调用OpenCV 的 PnP 求解，可选择EPNP，DLS等方法
  Mat R;
  cv::Rodrigues(r, R); // r为旋转向量形式，用Rodrigues公式转换为矩阵
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve pnp in opencv cost time: " << time_used.count() << " seconds." << endl;

  cout << "R=" << endl << R << endl;
  cout << "t=" << endl << t << endl;
  /********************************/

  VecVector3d pts_3d_eigen;
  VecVector2d pts_2d_eigen;
  //
  for (size_t i = 0; i < pts_3d.size(); ++i) {
	//图1的3D点
    pts_3d_eigen.push_back(Eigen::Vector3d(pts_3d[i].x, pts_3d[i].y, pts_3d[i].z));
	//图2的2D点
    pts_2d_eigen.push_back(Eigen::Vector2d(pts_2d[i].x, pts_2d[i].y));
  }

  //高斯牛顿法优化
  cout << "calling bundle adjustment by gauss newton" << endl;
  Sophus::SE3d pose_gn;
  t1 = chrono::steady_clock::now();
  bundleAdjustmentGaussNewton(pts_3d_eigen, pts_2d_eigen, K, pose_gn);
  t2 = chrono::steady_clock::now();
  time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve pnp by gauss newton cost time: " << time_used.count() << " seconds." << endl;

  //g2o优化
  cout << "calling bundle adjustment by g2o" << endl;
  Sophus::SE3d pose_g2o;
  t1 = chrono::steady_clock::now();
  bundleAdjustmentG2O(pts_3d_eigen, pts_2d_eigen, K, pose_g2o);
  t2 = chrono::steady_clock::now();
  time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "solve pnp by g2o cost time: " << time_used.count() << " seconds." << endl;
  return 0;
}

void find_feature_matches(const Mat &img_1, const Mat &img_2,
                          std::vector<KeyPoint> &keypoints_1,
                          std::vector<KeyPoint> &keypoints_2,
                          std::vector<DMatch> &matches) {
  //-- 初始化
  Mat descriptors_1, descriptors_2;
  // used in OpenCV3
  Ptr<FeatureDetector> detector = ORB::create();
  Ptr<DescriptorExtractor> descriptor = ORB::create();
  // use this if you are in OpenCV2
  // Ptr<FeatureDetector> detector = FeatureDetector::create ( "ORB" );
  // Ptr<DescriptorExtractor> descriptor = DescriptorExtractor::create ( "ORB" );
  Ptr<DescriptorMatcher> matcher = DescriptorMatcher::create("BruteForce-Hamming");
  //-- 第一步:检测 Oriented FAST 角点位置
  detector->detect(img_1, keypoints_1);
  detector->detect(img_2, keypoints_2);

  //-- 第二步:根据角点位置计算 BRIEF 描述子
  descriptor->compute(img_1, keypoints_1, descriptors_1);
  descriptor->compute(img_2, keypoints_2, descriptors_2);

  //-- 第三步:对两幅图像中的BRIEF描述子进行匹配，使用 Hamming 距离
  vector<DMatch> match;
  // BFMatcher matcher ( NORM_HAMMING );
  matcher->match(descriptors_1, descriptors_2, match);

  //-- 第四步:匹配点对筛选
  double min_dist = 10000, max_dist = 0;

  //找出所有匹配之间的最小距离和最大距离, 即是最相似的和最不相似的两组点之间的距离
  for (int i = 0; i < descriptors_1.rows; i++) {
    double dist = match[i].distance;
    if (dist < min_dist) min_dist = dist;
    if (dist > max_dist) max_dist = dist;
  }

  printf("-- Max dist : %f \n", max_dist);
  printf("-- Min dist : %f \n", min_dist);

  //当描述子之间的距离大于两倍的最小距离时,即认为匹配有误.但有时候最小距离会非常小,设置一个经验值30作为下限.
  for (int i = 0; i < descriptors_1.rows; i++) {
    if (match[i].distance <= max(2 * min_dist, 30.0)) {
      matches.push_back(match[i]);
    }
  }
}

Point2d pixel2cam(const Point2d &p, const Mat &K) {
  return Point2d
    (
      (p.x - K.at<double>(0, 2)) / K.at<double>(0, 0),
      (p.y - K.at<double>(1, 2)) / K.at<double>(1, 1)
    );
}

void bundleAdjustmentGaussNewton(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {
  typedef Eigen::Matrix<double, 6, 1> Vector6d;
  const int iterations = 10;
  double cost = 0, lastCost = 0;
  double fx = K.at<double>(0, 0);
  double fy = K.at<double>(1, 1);
  double cx = K.at<double>(0, 2);
  double cy = K.at<double>(1, 2);

  for (int iter = 0; iter < iterations; iter++) {
    Eigen::Matrix<double, 6, 6> H = Eigen::Matrix<double, 6, 6>::Zero();
    Vector6d b = Vector6d::Zero();

    cost = 0;
    // compute cost
    for (int i = 0; i < points_3d.size(); i++) {
	  //世界坐标转为相机坐标
      Eigen::Vector3d pc = pose * points_3d[i];
      double inv_z = 1.0 / pc[2];
      double inv_z2 = inv_z * inv_z;
	  //相机坐标转为像素坐标
      Eigen::Vector2d proj(fx * pc[0] / pc[2] + cx, fy * pc[1] / pc[2] + cy);

      Eigen::Vector2d e = points_2d[i] - proj;  //误差，观测值-预测值，反之取负

      cost += e.squaredNorm();  //误差里的每项平方和
      Eigen::Matrix<double, 2, 6> J;
	  //雅可比矩阵赋值
      J << -fx * inv_z,
        0,
        fx * pc[0] * inv_z2,
        fx * pc[0] * pc[1] * inv_z2,
        -fx - fx * pc[0] * pc[0] * inv_z2,
        fx * pc[1] * inv_z,
        0,
        -fy * inv_z,
        fy * pc[1] * inv_z2,
        fy + fy * pc[1] * pc[1] * inv_z2,
        -fy * pc[0] * pc[1] * inv_z2,
        -fy * pc[0] * inv_z;

      H += J.transpose() * J;
      b += -J.transpose() * e;
    }

    Vector6d dx;
    dx = H.ldlt().solve(b);

    if (isnan(dx[0])) {
      cout << "result is nan!" << endl;
      break;
    }

    if (iter > 0 && cost >= lastCost) {
      // cost increase, update is not good
      cout << "cost: " << cost << ", last cost: " << lastCost << endl;
      break;
    }

    // update your estimation
	//更新位姿
    pose = Sophus::SE3d::exp(dx) * pose;
    lastCost = cost;

    cout << "iteration " << iter << " cost=" << std::setprecision(12) << cost << endl;
    if (dx.norm() < 1e-6) {
      // converge
      break;
    }
  }

  cout << "pose by g-n: \n" << pose.matrix() << endl;
}

/// vertex and edges used in g2o ba
class VertexPose : public g2o::BaseVertex<6, Sophus::SE3d> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  virtual void setToOriginImpl() override {
    _estimate = Sophus::SE3d();
  }

  /// left multiplication on SE3
  virtual void oplusImpl(const double *update) override {
    Eigen::Matrix<double, 6, 1> update_eigen;
    update_eigen << update[0], update[1], update[2], update[3], update[4], update[5];
    _estimate = Sophus::SE3d::exp(update_eigen) * _estimate;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}
};

class EdgeProjection : public g2o::BaseUnaryEdge<2, Eigen::Vector2d, VertexPose> {
public:
  EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

  EdgeProjection(const Eigen::Vector3d &pos, const Eigen::Matrix3d &K) : _pos3d(pos), _K(K) {}

  virtual void computeError() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_pixel = _K * (T * _pos3d);
    pos_pixel /= pos_pixel[2];
    _error = _measurement - pos_pixel.head<2>();
  }

  virtual void linearizeOplus() override {
    const VertexPose *v = static_cast<VertexPose *> (_vertices[0]);
    Sophus::SE3d T = v->estimate();
    Eigen::Vector3d pos_cam = T * _pos3d;
    double fx = _K(0, 0);
    double fy = _K(1, 1);
    double cx = _K(0, 2);
    double cy = _K(1, 2);
    double X = pos_cam[0];
    double Y = pos_cam[1];
    double Z = pos_cam[2];
    double Z2 = Z * Z;
    _jacobianOplusXi
      << -fx / Z, 0, fx * X / Z2, fx * X * Y / Z2, -fx - fx * X * X / Z2, fx * Y / Z,
      0, -fy / Z, fy * Y / (Z * Z), fy + fy * Y * Y / Z2, -fy * X * Y / Z2, -fy * X / Z;
  }

  virtual bool read(istream &in) override {}

  virtual bool write(ostream &out) const override {}

private:
  Eigen::Vector3d _pos3d;
  Eigen::Matrix3d _K;
};

void bundleAdjustmentG2O(
  const VecVector3d &points_3d,
  const VecVector2d &points_2d,
  const Mat &K,
  Sophus::SE3d &pose) {

  // 构建图优化，先设定g2o
  typedef g2o::BlockSolver<g2o::BlockSolverTraits<6, 3>> BlockSolverType;  // pose is 6, landmark is 3
  typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
  // 梯度下降方法，可以从GN, LM, DogLeg 中选
  auto solver = new g2o::OptimizationAlgorithmGaussNewton(
    g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
  g2o::SparseOptimizer optimizer;     // 图模型
  optimizer.setAlgorithm(solver);   // 设置求解器
  optimizer.setVerbose(true);       // 打开调试输出

  // vertex
  VertexPose *vertex_pose = new VertexPose(); // camera vertex_pose
  vertex_pose->setId(0);
  vertex_pose->setEstimate(Sophus::SE3d());
  optimizer.addVertex(vertex_pose);

  // K
  Eigen::Matrix3d K_eigen;
  K_eigen <<
          K.at<double>(0, 0), K.at<double>(0, 1), K.at<double>(0, 2),
    K.at<double>(1, 0), K.at<double>(1, 1), K.at<double>(1, 2),
    K.at<double>(2, 0), K.at<double>(2, 1), K.at<double>(2, 2);

  // edges
  int index = 1;
  for (size_t i = 0; i < points_2d.size(); ++i) {
    auto p2d = points_2d[i];
    auto p3d = points_3d[i];
    EdgeProjection *edge = new EdgeProjection(p3d, K_eigen);
    edge->setId(index);
    edge->setVertex(0, vertex_pose);
    edge->setMeasurement(p2d);
    edge->setInformation(Eigen::Matrix2d::Identity());
    optimizer.addEdge(edge);
    index++;
  }

  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();
  optimizer.setVerbose(true);
  optimizer.initializeOptimization();
  optimizer.optimize(10);
  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();
  chrono::duration<double> time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);
  cout << "optimization costs time: " << time_used.count() << " seconds." << endl;
  cout << "pose estimated by g2o =\n" << vertex_pose->estimate().matrix() << endl;
  pose = vertex_pose->estimate();
}

CMakeLists.txt:

cmake_minimum_required(VERSION 2.8)
project(3d2d)

set(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11")
list(APPEND CMAKE_MODULE_PATH ${PROJECT_SOURCE_DIR}/cmake)
include_directories(inc)
aux_source_directory(src DIR_SRCS)
SET(SOUR_FILE ${DIR_SRCS})
find_package(OpenCV 3 REQUIRED)
find_package(G2O REQUIRED)
find_package(Sophus REQUIRED)

include_directories(
        ${OpenCV_INCLUDE_DIRS}
        ${G2O_INCLUDE_DIRS}
        ${Sophus_INCLUDE_DIRS}
        "/usr/include/eigen3/"
)

add_executable(3d2d ${SOUR_FILE})
target_link_libraries(3d2d ${OpenCV_LIBS})
target_link_libraries(3d2d g2o_core g2o_stuff)

cmake文件夹:FindG2O.cmake

# Find the header files

FIND_PATH(G2O_INCLUDE_DIR g2o/core/base_vertex.h
  ${G2O_ROOT}/include
  $ENV{G2O_ROOT}/include
  $ENV{G2O_ROOT}
  /usr/local/include
  /usr/include
  /opt/local/include
  /sw/local/include
  /sw/include
  NO_DEFAULT_PATH
  )

# Macro to unify finding both the debug and release versions of the
# libraries; this is adapted from the OpenSceneGraph FIND_LIBRARY
# macro.

MACRO(FIND_G2O_LIBRARY MYLIBRARY MYLIBRARYNAME)

  FIND_LIBRARY("${MYLIBRARY}_DEBUG"
    NAMES "g2o_${MYLIBRARYNAME}_d"
    PATHS
    ${G2O_ROOT}/lib/Debug
    ${G2O_ROOT}/lib
    $ENV{G2O_ROOT}/lib/Debug
    $ENV{G2O_ROOT}/lib
    NO_DEFAULT_PATH
    )

  FIND_LIBRARY("${MYLIBRARY}_DEBUG"
    NAMES "g2o_${MYLIBRARYNAME}_d"
    PATHS
    ~/Library/Frameworks
    /Library/Frameworks
    /usr/local/lib
    /usr/local/lib64
    /usr/lib
    /usr/lib64
    /opt/local/lib
    /sw/local/lib
    /sw/lib
    )

  FIND_LIBRARY(${MYLIBRARY}
    NAMES "g2o_${MYLIBRARYNAME}"
    PATHS
    ${G2O_ROOT}/lib/Release
    ${G2O_ROOT}/lib
    $ENV{G2O_ROOT}/lib/Release
    $ENV{G2O_ROOT}/lib
    NO_DEFAULT_PATH
    )

  FIND_LIBRARY(${MYLIBRARY}
    NAMES "g2o_${MYLIBRARYNAME}"
    PATHS
    ~/Library/Frameworks
    /Library/Frameworks
    /usr/local/lib
    /usr/local/lib64
    /usr/lib
    /usr/lib64
    /opt/local/lib
    /sw/local/lib
    /sw/lib
    )

  IF(NOT ${MYLIBRARY}_DEBUG)
    IF(MYLIBRARY)
      SET(${MYLIBRARY}_DEBUG ${MYLIBRARY})
    ENDIF(MYLIBRARY)
  ENDIF( NOT ${MYLIBRARY}_DEBUG)

ENDMACRO(FIND_G2O_LIBRARY LIBRARY LIBRARYNAME)

# Find the core elements
FIND_G2O_LIBRARY(G2O_STUFF_LIBRARY stuff)
FIND_G2O_LIBRARY(G2O_CORE_LIBRARY core)

# Find the CLI library
FIND_G2O_LIBRARY(G2O_CLI_LIBRARY cli)

# Find the pluggable solvers
FIND_G2O_LIBRARY(G2O_SOLVER_CHOLMOD solver_cholmod)
FIND_G2O_LIBRARY(G2O_SOLVER_CSPARSE solver_csparse)
FIND_G2O_LIBRARY(G2O_SOLVER_CSPARSE_EXTENSION csparse_extension)
FIND_G2O_LIBRARY(G2O_SOLVER_DENSE solver_dense)
FIND_G2O_LIBRARY(G2O_SOLVER_PCG solver_pcg)
FIND_G2O_LIBRARY(G2O_SOLVER_SLAM2D_LINEAR solver_slam2d_linear)
FIND_G2O_LIBRARY(G2O_SOLVER_STRUCTURE_ONLY solver_structure_only)
FIND_G2O_LIBRARY(G2O_SOLVER_EIGEN solver_eigen)

# Find the predefined types
FIND_G2O_LIBRARY(G2O_TYPES_DATA types_data)
FIND_G2O_LIBRARY(G2O_TYPES_ICP types_icp)
FIND_G2O_LIBRARY(G2O_TYPES_SBA types_sba)
FIND_G2O_LIBRARY(G2O_TYPES_SCLAM2D types_sclam2d)
FIND_G2O_LIBRARY(G2O_TYPES_SIM3 types_sim3)
FIND_G2O_LIBRARY(G2O_TYPES_SLAM2D types_slam2d)
FIND_G2O_LIBRARY(G2O_TYPES_SLAM3D types_slam3d)

# G2O solvers declared found if we found at least one solver
SET(G2O_SOLVERS_FOUND "NO")
IF(G2O_SOLVER_CHOLMOD OR G2O_SOLVER_CSPARSE OR G2O_SOLVER_DENSE OR G2O_SOLVER_PCG OR G2O_SOLVER_SLAM2D_LINEAR OR G2O_SOLVER_STRUCTURE_ONLY OR G2O_SOLVER_EIGEN)
  SET(G2O_SOLVERS_FOUND "YES")
ENDIF(G2O_SOLVER_CHOLMOD OR G2O_SOLVER_CSPARSE OR G2O_SOLVER_DENSE OR G2O_SOLVER_PCG OR G2O_SOLVER_SLAM2D_LINEAR OR G2O_SOLVER_STRUCTURE_ONLY OR G2O_SOLVER_EIGEN)

# G2O itself declared found if we found the core libraries and at least one solver
SET(G2O_FOUND "NO")
IF(G2O_STUFF_LIBRARY AND G2O_CORE_LIBRARY AND G2O_INCLUDE_DIR AND G2O_SOLVERS_FOUND)
  SET(G2O_FOUND "YES")
ENDIF(G2O_STUFF_LIBRARY AND G2O_CORE_LIBRARY AND G2O_INCLUDE_DIR AND G2O_SOLVERS_FOUND)