C. Tourist Problem 2021.3.29 晚vj拉题 cf 1600 纯数学题

拉题链接  https://vjudge.net/contest/430219#overview

原题链接  https://codeforces.com/problemset/problem/340/C

前言

cf 1600的题, 直接拿来给大一的做, 感觉有亿点点难, 这是个纯数学题, 我用的排列组合方法推导

题目

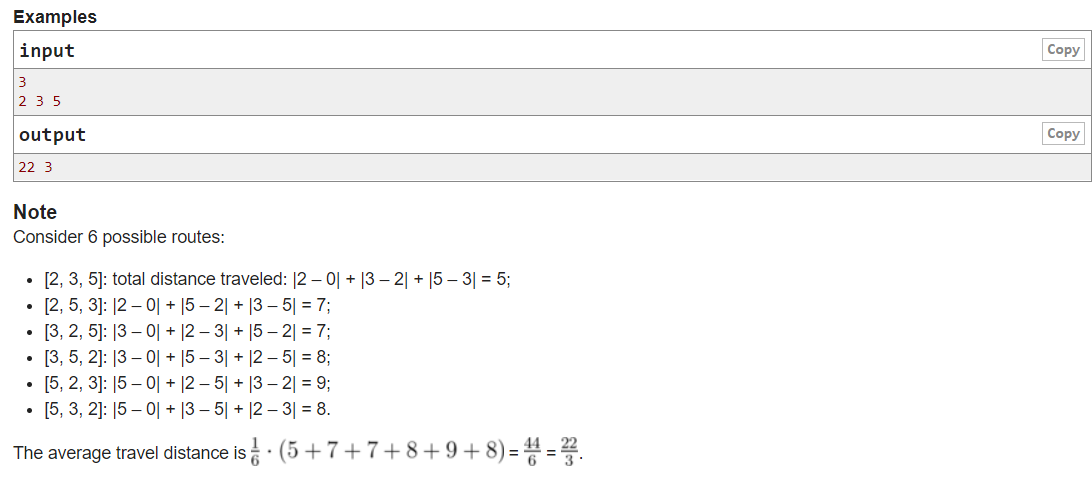
题意(其实我觉得还是看上边的Note好理解)

给n个数(分别为a₁, a₂ ...... a_n-1, 把这n个数全排(共A_nⁿ 个序列)一遍, 对于每个序列, 值=每个|a_i - a_i-1|之和(i = 1~n) , 其中, i = 0时, 为|a₁-0|

然后, 将这n的阶乘个式子的值加起来, 先用res表示, 最后输出res/g  和  A_nⁿ / g  (g为res与A_nⁿ 最大公因数)

题解

硬做会超时, 要想着归纳

一  : 当对于一种序列, 比如2 3 5(注意5在最后面): |2 – 0| + |3 – 2| + |5 – 3| = 5; 5只出现1次, 其余2 3都出现2次,

　　即: 一种序列中最后面的数出现一次, 前n-1个数出现2次

　　====> 在这所有排列中, 每个数出现总次数 =  2 * (n的阶乘) - (n-1的阶乘)

　　对式子的解释: 2 * (n的阶乘): 所有数全排的种类数 * 一种排列出现两次;  (n - 1的阶乘): 当这个数在最后时, 前面的数全排

二  : 先把绝对值拆开, 比如 |2 – 0| + |3 – 2| + |5 – 3| = 2 + 3 - 2 + 5 - 3 ,最大值5一定是正的, 3与2搭配时-->3为正; 3与5搭配时-->3为负

　　即: 一个数与比它大的数搭配(挨着,不分前后)时, 它为负, 与比它小的数搭配时, 它为正

　　====> 设大于n的数有m个, 减去一个数的次数(为负的次数) = 2 * m * (n - 1的阶乘) 

　　对式子的解释: 2为该数与另一个数的两种排列, m: 从m个比它大的数挑一个, 也就是C_m¹ ;  (n - 1的阶乘) : 该数与另一个数绑定后全排

重点来了, 结果快来了

---

这个数最后是加减了多少倍呢?

每个数出现的次数

= 正的次数 - 负的次数

= ( 出现的总次数 -  负的次数 )  -  负的次数 

= 第一个式子 - 2 * 第二个式子

= [2 * (n的阶乘) - (n-1的阶乘)] - [2 * ( 2 * m * (n - 1的阶乘) )]

那结果 = [ 2 * (n的阶乘) - (n-1的阶乘) - 2 *  2 * m * (n - 1的阶乘)  ]    和    n的阶乘   ~~~(约去n-1的阶乘)~~~

= 2 * n - 1 - 4 * m      和         n

m = 大于该数的个数, 对数组小到大排序后(下标从0开始), 大于该数的个数 = n - i - 1, 带入上式即可

(化简 = 2n-1-4n+4i+4 = 4i-2n+3)

代码

#include <iostream>
#include <algorithm>

using namespace std;

typedef long long ll;

const int N = 1e5 + 10;

ll res = 0, fenmu = 1;
ll a[N];

ll gcd(ll a, ll b)
{
    return b? gcd(b, a % b): a;
}
int main()
{
    int n;
    cin >> n;
    for(int i = 0; i < n; i ++)
        scanf("%lld", &a[i]);

    sort(a, a+n);
    for(int i = 0; i < n; i ++)
       res += (2 * n - 1 - 4 * (n - i - 1)) * a[i];
   //     res += (4i-2n+3) * a[i];
    int g = gcd(res, n);
    cout << res/g << ' '<< n/g << endl;
    return 0;
}