论文解读（DCN）《Towards K-means-friendly Spaces: Simultaneous Deep Learning and Clustering》

论文信息

论文标题：Towards K-means-friendly Spaces: Simultaneous Deep Learning and Clustering
论文作者：Bo Yang, Xiao Fu, Nicholas D. Sidiropoulos, Mingyi Hong
论文来源：2016, ICML
论文地址：download
论文代码：download

1 Introduction

　　为了恢复“聚类友好”的潜在表示并更好地聚类数据，我们提出了一种联合 DR (dimensionality reduction) 和 K-means 的聚类方法，通过学习深度神经网络(DNN)来实现 DR。

2 Background and Related Works

2.1 Kmeans

　　给定样本集 $\left\{\boldsymbol{x}_{i}\right\}_{i=1, \ldots, N}$ ，$\boldsymbol{x}_{i} \in \mathbb{R}^{M}$。聚类的任务是将 $N$ 个数据样本分成 $K$ 类。

　　K-Means 优化的是下述损失函数：

　　　　$\begin{array}{l}\underset{\boldsymbol{M} \in \mathbb{R}^{M \times K},\left\{\boldsymbol{s}_{i} \in \mathbb{R}^{K}\right\}}{\text{min}} \quad & \sum_{i=1}^{N}\left\|\boldsymbol{x}_{i}-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2} \\\text { s.t. } & s_{j, i} \in\{0,1\}, \mathbf{1}^{T} \boldsymbol{s}_{i}=1 \quad \forall i, j,\end{array}  \quad\quad\quad(1)$

　　其中，

• • $\boldsymbol{s}_{i}$ 是样本 $x_i$ 的聚类分配向量；
  • $s_{j, i}$ 是 $\boldsymbol{s}_{i}$ 的第 $j$ 个元素；
  • $\boldsymbol{m}_{k}$ 代表着第 $k$ 个聚类中心；

2.2 joint DR and Clustering

　　考虑生成模型的数据样本生成 $\boldsymbol{x}_{i}=\boldsymbol{W} \boldsymbol{h}_{i}$，其中 $\boldsymbol{W} \in \mathbb{R}^{M \times R}$ 、$\boldsymbol{h}_{i} \in \mathbb{R}^{R}$，并且 $R \ll M$ 。假设数据集群在潜在域中被很好地分离出来 ( $\boldsymbol{h}_{i}$)
，联合优化问题如下：

　　　　$\begin{array}{l}\underset{\boldsymbol{M},\left\{\boldsymbol{s}_{i}\right\}, \boldsymbol{W}, \boldsymbol{H}}{\text{min }}&\|\boldsymbol{X}-\boldsymbol{W} \boldsymbol{H}\|_{F}^{2}+\lambda \sum\limits_{i=1}^{N}\left\|\boldsymbol{h}_{i}-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2} \quad+r_{1}(\boldsymbol{H})+r_{2}(\boldsymbol{W}) \\\text { s.t. } &s_{j, i} \in\{0,1\}, \mathbf{1}^{T} \boldsymbol{s}_{i}=1 \forall i, j,\end{array}$

　　其中，$r_1$ 和 $r_2$ 是正则化项；

　　

3 Method

　　目标函数：

　　　　$\begin{array}{l} \underset{\mathcal{W}, \mathcal{Z},\mathcal{M},{s_i}}{\text{min}}& \sum_{i=1}^{N}\left(\ell\left(\boldsymbol{g}\left(\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)\right), \boldsymbol{x}_{i}\right)+\frac{\lambda}{2}\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2}\right)\\\text { s.t. }  &\quad s_{j, i} \in\{0,1\}, \quad  \mathbf{1}^{T} s_{i}=1 \quad\forall i, j \end{array}$

　　 其中：

• • $\ell(\boldsymbol{x}, \boldsymbol{y})=\|\boldsymbol{x}-\boldsymbol{y}\|_{2}^{2}$，同时也可以考虑 $l_1-norm$ ，或者 KL 散度；
  • $f$ 和 $g$ 分别代表编码和解码的过程；

　　算法框架：

　　

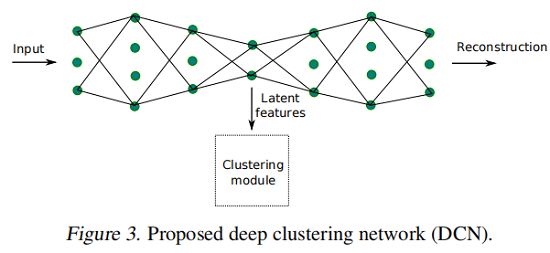
4 Optimization Procedure

4.1. Initialization via Layer-wise Pre-Training

　　首先通过预训练自编码器得到潜在表示（bottleneck layer 的输出），然后在潜在表示上使用 K-means 得到聚类中心 $\boldsymbol{M}$ 和聚类分配向量 $s_{i}$。

4.2. Alternating Stochastic Optimization

4.2.1 Update network parameters

　　固定 $\left(M,\left\{s_{i}\right\}\right)$，优化 $(\mathcal{W}, \mathcal{Z})$，那么该问题变为：

　　　　$\underset{\mathcal{W}, \mathcal{Z}}{\text{min }} L^{i}=\ell\left(\boldsymbol{g}\left(\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)\right), \boldsymbol{x}_{i}\right)+\frac{\lambda}{2}\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)-\boldsymbol{M} \boldsymbol{s}_{i}\right\|_{2}^{2}$

　　对于 $(\mathcal{W}, \mathcal{Z})$ 的更新可以借助于反向传播。

4.2.2 Update clustering parameters

　　固定网络参数和聚类质心矩阵 $M$，当前样本的聚类分配向量 $s_i$：

　　　　$s_{j, i} \leftarrow\left\{\begin{array}{ll}1, & \text { if } j=\underset{k=\{1, \ldots, K\}}{\arg \min }\left\|\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)-\boldsymbol{m}_{k}\right\|_{2}, \\0, & \text { otherwise }\end{array}\right.$

　　当固定 $\boldsymbol{s}_{i}$ 和 $\mathcal{X}=(\mathcal{W}, \mathcal{Z})$ 时，更新 $M$ :

　　　　$\boldsymbol{m}_{k}=\left(1 /\left|\mathcal{C}_{k}^{i}\right|\right) \sum\limits_{i \in \mathcal{C}_{k}^{i}} \boldsymbol{f}\left(\boldsymbol{x}_{i}\right)$

　　其中，$\mathcal{C}_{k}^{i}$ 是分配给从第一个样本到当前样本 $i$ 的聚类 $k$ 的样本的记录索引集。

　　虽然上面的更新是直观的，但对于在线算法来说可能是有问题的，因为已经出现的历史数据(即 $\boldsymbol{x_{1}}, \ldots, \boldsymbol{x}_{i}$)可能不足以建模全局集群结构，而初始 $s_i$ 可能远远不正确。

　　因此，简单地平均当前分配的样本可能会导致数值问题。我们没有做上述操作，而是使用(Sculley，2010)中的想法自适应地改变更新的学习速率来更新 $\boldsymbol{m}_{1}, \ldots, \boldsymbol{m}_{K}$。

　　直觉很简单：假设 cluster 在包含的数据样本数量上是大致是平衡的。然后，在为多个样本更新 $M$ 之后，应该更优雅地更新已经有许多分配成员的集群的质心，同时更积极地更新其他成员，以保持平衡。为了实现这一点，让 $c_{k}^{i}$ 是算法在处理传入的样本 $x_i$ 之前分配一个样本给集群 $k$ 的次数，并通过一个简单的梯度步骤更新 $m_k$：

　　　　$\boldsymbol{m}_{k} \leftarrow \boldsymbol{m}_{k}-\left(1 / c_{k}^{i}\right)\left(\boldsymbol{m}_{k}-\boldsymbol{f}\left(\boldsymbol{x}_{i}\right)\right) s_{k, i}\quad\quad\quad(8)$

　　其中，$1 / c_{k}^{i}$ 用于控制学习率。上述 $M$ 的更新也可以看作是一个SGD步骤，从而产生了在 Algorithm 1 中总结的一个整体的交替块SGD过程。请注意，一个 epoch 对应于所有数据样本通过网络的传递。

　　

5 Experiments

聚类

　　

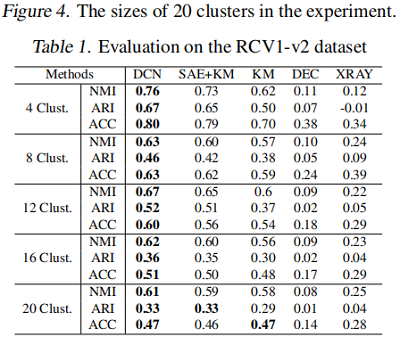
6 Conclusion

　　在这项工作中，我们提出了一种联合DR和K-means聚类方法，其中DR部分是通过学习一个深度神经网络来完成的。我们的目标是自动将高维数据映射到一个潜在的空间，其中K-means是一个合适的聚类工具。我们精心设计了网络结构，以避免琐碎和无意义的解决方案，并提出了一个有效的和可扩展的优化程序来处理所制定的具有挑战性的问题。综合和实际数据实验表明，该算法在各种数据集上都非常有效。

修改历史

2022-06-28 创建文章

论文解读目录