时间序列分析2.X AR与MA

ARMA与ARIMA模型

对平稳时间序列和非平稳时间序列，分别假定适当的 ARMA 模型和 ARIMA 模型

对非平稳时间序列建立 ARIMA 模型，实际上是通过先用适当的变换将非平稳序列转化为平稳序列，然后再建立 ARMA 模型

差分消除趋势性和季节性

将非平稳序列化为平稳序列的常见变换

• 趋势差分以消除趋势性
• 季节差分以消除季节性
• Box-Cox 变换以使得波动稳定化

趋势差分

\(y_{t}=x_{t}-x_{t-1}=\nabla x_{t}\)

季节差分

\(y_{t}=x_{t}-x_{t-s}=\nabla_{s} x_{t}\)

s 常取12

当序列同时有趋势性与周期性时,先趋势差分,再季节差分 \(z_{t}=\nabla_{12} y_{t}=\nabla_{12} \nabla x_{t}\)

对于波动随时间变化的序列变为平稳序列

• 先做适当的 Box-Cox 变换，使得其波动稳定化，然后再进行差分运算消除趋势性和季节性
• 先取对数,再趋势差分,最后季节差分
  
  \(w_{t}=\nabla_{12} \nabla \ln x_{t}\)

平稳过程

弱平稳过程

定义

满足:

• \(E\left(X_{t}^{2}\right)<\infty\)
• \(E\left(X_{t}\right)\) 为常数
• \(\operatorname{Cov}\left(X_{t}, X_{t-k}\right)\) 与 \(t\) 无关, \(\forall k\)

即称为弱平稳过程

性质

• \(k=0, Var(X_t)=\sigma^2, \forall t\) (波动不会随时间变化)
• \(\forall s<t,\operatorname{Cov}(X_t,X_s)=\operatorname{Cov}(X_t,X_{t-(t-s)})\) 只与 \(t-s\) 有关
• \(\operatorname{Corr}(X_t,X_s)\) 两点相关性只与间隔有关.(由此可以用昨天到今天的规律,根据今天的情况预测明天)

白噪声过程

满足:

• \(E\left(X_{t}\right)=\mu~, \forall t\)
• \(\operatorname{Var}\left(X_{t}\right)=\sigma^{2}~, \forall t\)
• \(\operatorname{Cov}\left(X_{t}, X_{s}\right)=0~, \forall t \neq s\)
• 不必相互独立

称为白噪声过程, \(Z_{t} \sim W N\left(0, \sigma_{Z}^{2}\right)\)

性质

• 满足 \(\rho_k=0,~\forall k\geq1\) ,即无序列相关性

随机漫步(RW)

随机漫步

定义

如果 \(X_{t}=X_{t-1}+Z_{t}\)

经过地推可以得到 \(X_{t}=X_{0}+Z_{1}+Z_{2}+\cdots+Z_{t}\)

性质

假设 \(X_0=0\), 对于随机漫步而言,

\[E\left(X_{t}\right)=0 ; \operatorname{Var}\left(X_{t}\right)=t \sigma_{Z}^{2}
\]

与 \(t\) 有关, 故不是平稳过程

带漂移项的随机漫步

定义

如果 \(X_{t}=\mu+X_{t-1}+Z_{t}\)

经过推导可得

\[X_{t}=X_{0}+t \mu+\sum_{i=1}^{t} Z_{i}
\]

性质

假设 \(X_0=0\), 对于带漂移项的随机漫步而言,

\[E\left(X_{t}\right)=t\mu ; \operatorname{Var}\left(X_{t}\right)=t \sigma_{Z}^{2}
\]

与 \(t\) 有关, 故不是平稳过程

ACF 及序列相关性的度量

ACF

延迟 k 自协方差函数

\(\gamma_{X}(k)=\operatorname{Cov}\left(X_{t}, X_{t-k}\right)\)

延迟 k 自相关函数

\[\rho(k)=\frac{\gamma_{X}(k)}{\gamma_{X}(0)}
\]

\(\rho(k)\) 常记作 \(\rho_k\)

ACF性质

• \(\rho(0)=1\)
• \(\rho(-k)=\rho(k)\)
• \(|\rho(k)|\leq 1\)

样本自相关函数

间隔 k 的相关系数

\[\hat{\rho}_{k}=\frac{\hat{\gamma}_k}{\hat{\gamma}_0}= \frac{\sum_{t=1}^{T-k}\left(x_{t}-\bar{x}\right)\left(x_{t+k}-\bar{x}\right)}{\sum_{t=1}^{T}\left(x_{t}-\bar{x}\right)^{2}}
\]

自相关图

以延迟阶数 \(k\) 为横坐标, \(\hat{\rho}_k\) 为纵坐标绘图

AR自回归模型

\(p\) 阶自回归过程 \(AR(p)\)

满足 \(X_{t}=\phi_{1} X_{t-1}+\phi_{2} X_{t-2}+\cdots+\phi_{p} X_{t-p}+Z_{t}\) 的平稳的 \(\{X_t\}\) 称为

(中心化的) \(p\) 阶自回归过程, 记为 \(AR(p)\)

一般的 \(AR(p)\) 可以表示为 \(X_{t}-\mu=\phi_{1}\left(X_{t-1}-\mu\right)+\phi_{2}\left(X_{t-2}-\mu\right)+\cdots+\phi_{p}\left(X_{t-p}-\mu\right)+Z_{t}\)

其可以等价展开成 \(X_{t}=\phi_{0}+\phi_{1} X_{t-1}+\phi_{2} X_{t-2}+\cdots+\phi_{p} X_{t-p}+Z_{t}\) ,

其中 \(\phi_{0}=\mu(1-\phi_1-\cdots-\phi_p)\)

\(AR(1)\)

模型样式

\(X_t=\phi X_{t-1}+Z_t\)

性质

由于 \(\{X_t\}\) 与 \(\{X_t-\mu\}\) 有相同的方差与协方差, 故我们可以令 \(\mu=0\)

容易验证,当 \(\phi<1\) 时,

对模型重复进行迭代, 我们有

\[\begin{aligned}
X_{t} &=\phi\left(\phi X_{t-2}+Z_{t-1}\right)+Z_{t}=\phi^{2} X_{t-2}+\phi Z_{t-1}+Z_{t} \\
&=\phi^{2}\left(\phi X_{t-3}+Z_{t-2}\right)+\phi Z_{t-1}+Z_{t}=\phi^{3} X_{t-3}+\phi^{2} Z_{t-2}+\phi Z_{t-1}+Z_{t}\\
&=\cdots
\end{aligned}
\]

一直进行下去,如果 \(|\phi|<1\) 容易验证其为平稳序列, 且其ACF函数为

\[\gamma_{X}(k)=\sum_{i=0}^{\infty} \phi^{i} \phi^{i+k}= \frac{\phi^{k}}{1-\phi^{2}}
\]

Xt 可以表示为当前和过去时刻扰动的收敛线性组合，即 \(MA(\infty)\) 形式，此时称 Xt 是因果过程。我们也可以得出结论: \(AR(1)\) 是因果平稳的充要条件是 \(|\phi|<1\)

期望与ACF

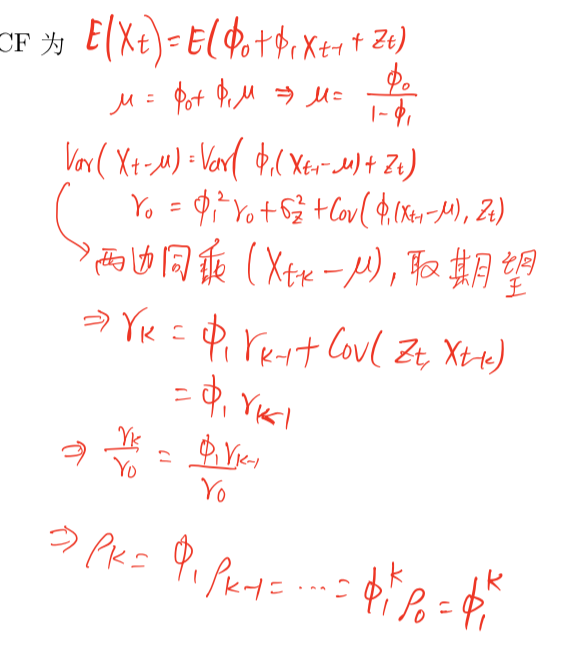
\(AR(2)\)

模型表示

\[\begin{array}{c}
X_{t}=\phi_{1} X_{t-1}+\phi_{2} X_{t-2}+Z_{t} \\
\left(1-\phi_{1} B-\phi_{2} B^{2}\right) X_{t}=Z_{t}
\end{array}\]

因果平稳条件

\[\phi(B)=1-\phi_{1} B-\phi_{2} B^{2}=\left(1-\pi_{1} B\right)\left(1-\pi_{2} B\right)
\]

\(\pi_1\) , \(\pi_2\) 为 \(\phi(B)=0\) 的两个根的倒数

令 \((1-\pi_2B)X_t=Y_t\) , 有 \((1-\pi_1B)Y_t=Z_t\)

当 \(|\pi_1|<1\) , \(\{Y_t\}\) 为因果平稳过程

当 \(|\pi_2|<1\) , \(X_t\) 可表示为 $$X_{t}=\sum_{j=0}^{\infty} \pi_{2}^{j} Y_{t-j}$$

也为因果平稳过程

所以, AR(2) 为因果平稳过程的条件是 \(\phi(B)=0\) 的两个根在单位圆外, 即 \(|\pi_1|<1\) , \(|\pi_2|<1\)

ACF

\(X_{t}=\phi_{1} X_{t-1}+\phi_{2} X_{t-2}+Z_{t}\) (为方便研究, 无妨设 \(\mu=0\))

两边同时乘以 \(X_{t-k}\) 并取期望

有 \(\gamma_{k}=\phi_{1} \gamma_{k-1}+\phi_{2} \gamma_{k-2}\)

再两边同除以 \(\gamma_{0}\) , 可得到

\(\rho_{k}=\phi_{1} \rho_{k-1}+\phi_{2} \rho_{k-2}, \forall k>0\)

令 \(k=1\), 利用 \(\rho_{-1}=\rho_{1}, \rho_{0}=1\), 有

\[\rho_1=\phi_1\rho_0+\phi_2\rho_1 \Rightarrow \rho_1=\phi_1+\phi_2\rho_1 \Rightarrow \rho_1=\frac{\phi_1}{1-\phi_2}
\]

由 \(\rho_{k}=\phi_{1} \rho_{k-1}+\phi_{2} \rho_{k-2}, \forall k>0\) , 与 \(\rho_1=\frac{\phi_1}{1-\phi_2}~, \rho_{0}=1\) ,可以计算任意阶延迟的ACF

平均周期长度

\(1-\phi_{1} B-\phi_{2} B^{2}=0\) 特征方程为 \(y^{2}-\phi_{1} y-\phi_{2}=0\)

若特征方程的根为共轭复特征根

记为 \(a\pm bi\)

则平均周期长度

\[k=\frac{2 \pi}{\cos ^{-1}[a / \sqrt{a^{2}+b^{2}}]}
\]

\(AR(p)\)

AR建模

步骤

• 确保对象为平稳序列
• 定阶
• 估计参数
• 残差诊断
• 优化
• 预测

定阶

PACF定阶

定义

\(PACF=Corr(X_t,X_{t-k}|X_{t-1},X_{t-2},\cdots,X_{t-k+1})\)

通过PACF图在 \(p\) 处截尾, 选取 \(p\)

信息准则定阶

• 赤池信息准则 (AIC)
• 贝叶斯信息准则 (BIC)

MA移动平均模型

\(MA(q)\)定义

满足 \(X_{t}=\mu+Z_{t}+\theta_{1} Z_{t-1}+\theta_{2} Z_{t-2}+\cdots+\theta_{q} Z_{t-q}\) 的平稳过程

性质

平稳性

不需要系数满足额外的限制条件，\(MA\) 模型总是因果平稳的

\(E\left(X_{t}\right)=\mu ; \quad \operatorname{Var}\left(X_{t}\right)=\sigma_{Z}^{2}\left(1+\theta_{1}^{2}+\cdots+\theta_{q}^{2}\right)\)

以及 \(\operatorname{Cov}\left(X_{t}, X_{t-k}\right)\) 均与 \(t\) 无关;

ACF

\[\operatorname{Cov}(X_{t}, X_{t-k})=\left\{\begin{array}{lr}
(1+\theta_{1}^{2}+\cdots+\theta_{q}^{2}) \sigma_{Z}^{2} & k=0 \\
(\sum_{i=0}^{q-k} \theta_{i} \theta_{i+k}) \sigma_{Z}^{2} & 1 \leq k \leq q \\
0 & k>q
\end{array}\right\}\]

这里记 \(\theta_{0}=1\) 。

于是, \(M A(q)\) 过程的 \(ACF\) 为

\[\rho_{k}=\frac{\gamma_{k}}{\gamma_{0}}=\left\{\begin{array}{lc}
1 & k=0 \\
\frac{\sum_{i=0}^{q-k} \theta_{i} \theta_{i+k}}{1+\theta_{1}^{2}+\cdots+\theta_{q}^{2}} & 1 \leq k \leq q \\
0 & k>q
\end{array}\right.\]

可逆性

定义

如果 \(t\) 时刻的随机扰动可以表示为当前值和历史值的一个收敛和的形式，即

\(Z_{t}=\sum_{j=0}^{\infty} \pi_{j} X_{t-j}\)

其中, \(\pi_{0}=1, \sum\left|\pi_{j}\right|<\infty\) .

形式

\[\begin{array}{c}
X_{t}=\theta(B) Z_{t} \stackrel{可逆}{==} Z_{t}=X_{t}+\pi X_{t+1}=\pi(B) X_{t} \\
\theta(B) \pi(B)=1
\end{array}\]

MA建模

定阶

通过ACF图在 \(q\) 处截尾, 选取 \(q\)