2022-11-11 Acwing每日一题

本系列所有题目均为Acwing课的内容，发表博客既是为了学习总结，加深自己的印象，同时也是为了以后回过头来看时，不会感叹虚度光阴罢了，因此如果出现错误，欢迎大家能够指出错误，我会认真改正的。同时也希望文章能够让你有所收获，与君共勉！

昨天写了一道表达式求值就已经快寄了，今天要写的队列，单调栈，单调队列就比较好写了，还好都是模板。

模拟队列

实现一个队列，队列初始为空，支持四种操作：

push x – 向队尾插入一个数 x；

pop – 从队头弹出一个数；

empty – 判断队列是否为空；

query – 查询队头元素。

现在要对队列进行 M 个操作，其中的每个操作 3 和操作 4 都要输出相应的结果。

输入格式

第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令为 push x，pop，empty，query 中的一种。

输出格式

对于每个 empty 和 query 操作都要输出一个查询结果，每个结果占一行。

其中，empty 操作的查询结果为 YES 或 NO，query 操作的查询结果为一个整数，表示队头元素的值。

数据范围

1≤M≤100000,

1≤x≤109,

所有操作保证合法。

输入样例：

10 push 6 empty query pop empty push 3 push 4 pop query push 6

输出样例：

NO 6 YES 4

算法原理

队列就一般只需要四个操作，这里我们使用数组来模拟队列q，定义两个指针head和tail。

初始化head = 0,tail = -1;

1. 入队

q[tail++] = x;

1. 出队

head++;

1. 判断长度

size = tail - head + 1;

1. 判断为空

if(tail - head + 1 == 0)

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int q[N],head,tail;
int n;
int main()
{
    cin >> n;
    head = 0,tail = -1;
    while(n--){
        int x;
        string s;
        cin >> s;
        if(s == "push"){
            cin >> x;
            q[++tail] = x;
        }
        else if(s == "query"){
            cout << q[head] << endl;
        }
        else if(s == "pop"){
            head ++ ;
        }
        else if(s == "empty"){
            if(tail - head + 1 == 0){
                cout << "YES" << endl;
            }
            else{
                cout << "NO" << endl;
            }
        }
    }
    return 0;
}

看，是吧，是不是很简单啊！

---

单调栈

给定一个长度为 N 的整数数列，输出每个数左边第一个比它小的数，如果不存在则输出 −1。

输入格式

第一行包含整数 N，表示数列长度。

第二行包含 N 个整数，表示整数数列。

输出格式

共一行，包含 N 个整数，其中第 i 个数表示第 i 个数的左边第一个比它小的数，如果不存在则输出 −1。

数据范围

1≤N≤105

1≤数列中元素≤109

输入样例：

5

3 4 2 7 5

输出样例：

-1 3 -1 2 2

算法原理

或许我们也需要先使用暴力尝试去求解，双重循环，外层用变量i遍历这个数列，内层用j从i-1处向数组头方向进行搜索，第一个符合条件的就是我们需要的结果，时间复杂度为\(O(n\times n!)\)，时间复杂度再某些情况下有点高，因此我们需要对他进行优化，当然也可以优化，就是使用单调栈实现，下面就来看看单调栈是什么。

顾名思义，单调栈就是存储数值呈现单调递增或单调递减的栈，其主要用法就是求左边或右边的第一个比他大或比他小的元素，过程如下。



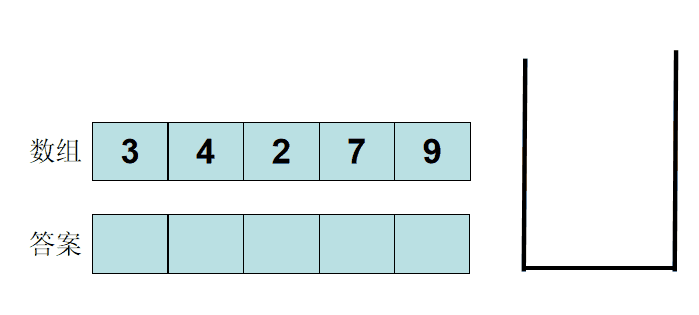
当我们需要得到左边第一个比他小的数时，我们应该知道在这个过程中那些对我们是有利的信息，那些是无用的信息，进一步可以发现那些可能是比他小的数，那些一定不会是比他小的数，对于一定不是比它小的数，我们可以不去搜索他，对于比他小的数，我们又该以怎样的一个搜索方式去寻找，那必然是需要速度快的搜索方式吧，因此我们可以使用单调栈取存储过去的那些元素，并再栈里面进行寻找。

• 因为我们需要比它小的，所以对于比它大的元素我们就要把他从栈中去掉
• 因为我们需要更快速的寻找，所以我们需要用利用单调性去搜索(而不必一一遍历)，且应该是单调递增，这时候我们会发现当我们需要第一个比他小的元素时，由于栈的后进先出原则，从栈顶往栈底寻找的第一个比他小的元素就是所需要的元素。注：不管找得到还是找不到当前元素左边第一个比它小的元素，我们都需要把他加进栈中，知道某一个元素比他小，把他移除栈
• 同理，找到当前元素左边第一个比它大的元素需要一个单调递减的栈。如果需要右边第一个比他小的元素，我们可以逆序遍历使用单调递增的栈，如果需要右边第一个比它大的元素，依然是逆序遍历使用单调递减的栈。

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int stk[N],top;
int a[N];
int main()
{
    int n;
    cin >>n ;
    for(int i=0; i < n ; ++i)   cin >> a[i];
    for(int i=0; i < n ; ++i){
        while(top && stk[top] >= a[i])	top--;
        if(top){
            cout << stk[top]  << " " ;
         }
        else{
            cout << "-1 " ;
        }
        stk[++top] = a[i];
    }
    return 0;
}

相信各位已经理解了吧！

---

单调队列

其实也就是滑动窗口。

给定一个大小为 n≤106 的数组。

有一个大小为 k 的滑动窗口，它从数组的最左边移动到最右边。

你只能在窗口中看到 k 个数字。

每次滑动窗口向右移动一个位置。

以下是一个例子：

该数组为 [1 3 -1 -3 5 3 6 7]，k 为 3。

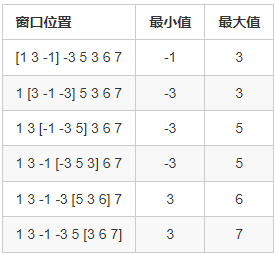
你的任务是确定滑动窗口位于每个位置时，窗口中的最大值和最小值。

输入格式

输入包含两行。

第一行包含两个整数 n 和 k，分别代表数组长度和滑动窗口的长度。

第二行有 n 个整数，代表数组的具体数值。

同行数据之间用空格隔开。

输出格式

输出包含两个。

第一行输出，从左至右，每个位置滑动窗口中的最小值。

第二行输出，从左至右，每个位置滑动窗口中的最大值。

输入样例：

8 3

1 3 -1 -3 5 3 6 7

输出样例：

-1 -3 -3 -3 3 3

3 3 5 5 6 7

算法原理

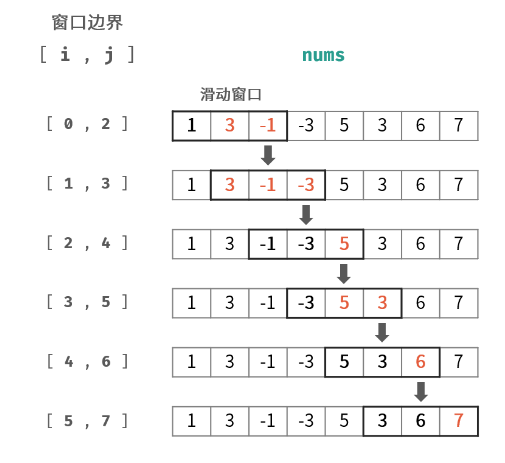
跟单调栈的原理类似，单调队列就是具有单调递增或单调递减的队列。需要注意的是单调队列里存储的时数组元素的下标。

我们先寻找暴力解法，然后寻找在这个过程中那些是我们不需要的元素，然后想办法使用单调队列进行优化，我们把每一个数都会推进队列和窗口里，当窗口里的元素足够时才会进行输出，当我们要输出最小值时，我们需要先形成一个单调递增队列，对于队列里比将要入队的元素要大的那些元素，我么需要将他移出队列（毕竟要最小的，如果比将要入队的元素还要小，那以后无论如何都不会选择他们的），这也保证了队列始终是单调递增的，因此队首所对应的元素一定是最小值。注：每一个将要进队列的元素也都要进入队列的

代码实现

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 1000010;
int q[N],head,tail;
int n,k;
int a[N];
int main()
{
    cin >> n >> k;
    for(int i=0 ;i < n ; ++i)   cin >> a[i];
    for(int i=0; i < n ; ++i){  // 窗口里的最小值
        while(head <= tail && q[head] < i-k+1)  ++head; // 队首不在窗口里面，就用队首指针
        while(head <= tail && a[q[tail]] >= a[i])    --tail; // 队列队尾元素比入队元素要大或者相等就出队（严格单调是不会有两个相等的元素）
        q[++tail] = i;
        if(i>=k-1){ // 如果窗口达到最大长度就开始输出最小值
            printf("%d ",a[q[head]]);
        }
    }
    cout << endl;
    head = 0,tail = -1;
    for(int i=0; i < n ; ++i){  // 窗口里的最大值
        while(head <= tail && q[head] < i-k+1)  ++head;
        while( head <= tail && a[q[tail]] <= a[i])  --tail;
        q[++tail] = i;
        if(i>=k-1)   printf("%d ",a[q[head]]);    
    }
    return 0;
}

终于写完啦，太不容易辣！