JavaScript实现二叉树算法
二叉树的遍历方式
分别为中序遍历(左子树->当前节点->右子树)、前序遍历(当前节点->左子树->右子树)、后序遍历(左子树->右子树->当前节点)。下面使用JavaScript语言实现二叉树的三种遍历算法。
首先构造一个排序二叉树(即满足左子节点比父节点小,右子节点比父节点大的二叉树),然后对其分别进行中序、前序、后序遍历。
排序二叉树结构图如下图所示:
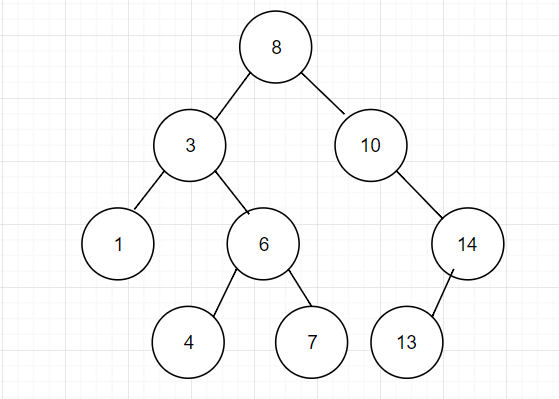
说明:
其中8为根节点(没有父节点的节点),4,、7、13为叶子节点(最后一层上没有子节点的节点),3、10、1、6、14为中间节点。
该树的最大深度为4(共4层)。
具体代码:
<!DOCTYPE html>
<html lang="en">
<head>
<title>javaScript实现二叉树算法</title>
</head>
<body>
<script type="text/javascript"> function BinaryTree(){
var Node = function(key) {//定义节点,包括父节点,左子节点,右子节点
this.key = key;//传入的元素值作为父节点
this.left = null;//左子节点初始为null
this.right = null;//右子节点初始为null
}; var root = null;//设置根节点初始值为空 // 定义插入节点函数,入参为当前节点和新加的节点
var insertNode = function(node, newNode) {
if (newNode.key < node.key) {//若新节点的父节点值小于的当前的节点的父节点值,则往左半部分走
if (node.left === null) {//当前节点若没有左子节点,则新节点作为当前节点的左子节点
node.left = newNode;
} else {//若当前节点的左子节点存在,则递归调用插入节点函数
insertNode(node.left, newNode);
}
} else {//若新节点的父节点值不小于当前节点的父节点值,则往右半部分走
if (node.right === null) {//若当前节点的右子节点不存在,则新节点作为当前节点的右子节点
node.right = newNode;
} else {//若当前节点的右子节点存在,则递归调用插入节点函数
insertNode(node.right, newNode);
}
}
}; this.insert = function(key) {//定义插入节点函数
var newNode = new Node(key);//定义新节点
if (root === null) {//若根节点为空,则新节点作为根节点
root = newNode;
} else {//若根节点存在,则执行插入节点函数
insertNode(root, newNode);
}
};
//中序遍历:左子树->当前节点->右子树,结果是一个升序有序序列
var inOrderTraverseNode = function(node, callback) {
if (node !== null) {//当前节点存在
inOrderTraverseNode(node.left, callback);//遍历左子树
callback(node.key);//执行回调函数
inOrderTraverseNode(node.right, callback);//遍历右子树
}
} this.inOrderTraverse = function(callback) {
inOrderTraverseNode(root, callback);
} //前序遍历:当前节点->左子树->右子树,常用于复制一个二叉树,效率高。
var preOrderTraverseNode = function(node, callback) {
if (node !== null) {//当前节点不为空
callback(node.key);//执行回调函数
preOrderTraverseNode(node.left, callback);//遍历左子树
preOrderTraverseNode(node.right, callback);//遍历右子树
}
} this.preOrderTraverse = function(callback) {
preOrderTraverseNode(root, callback);
} //后序遍历:左子树->右子树->当前节点,常用于文件系统遍历
var postOrderTraverseNode = function(node, callbakc) {
if (node !== null) {//当前节点不为空
postOrderTraverseNode(node.left, callback);//遍历左子树
postOrderTraverseNode(node.right, callback);//遍历右子树
callback(node.key);//执行回调函数
}
} this.postOrderTraverse = function(callback) {
postOrderTraverseNode(root, callback);
}
}
//测试二叉树排序
var nodes = [8, 3, 10, 1, 6, 14, 4, 7, 13];
var binaryTree = new BinaryTree();//实例化一个新的二叉树
nodes.forEach(function(key) {//遍历数组中的所有元素,执行二叉树排序操作,生成排序二叉树
binaryTree.insert(key);
});
//回调函数
var callback = function(key) {
console.log(key);//打印出当前节点值
}
//中序遍历测试
binaryTree.inOrderTraverse(callback);
//前序遍历测试
binaryTree.preOrderTraverse(callback);
//后序遍历测试
binaryTree.postOrderTraverse(callback); </script>
</body>
</html>
JavaScript实现二叉树算法的更多相关文章
- javascript数据结构与算法-- 二叉树
javascript数据结构与算法-- 二叉树 树是计算机科学中经常用到的一种数据结构.树是一种非线性的数据结构,以分成的方式存储数据,树被用来存储具有层级关系的数据,比如文件系统的文件,树还被用来存 ...
- javascript数据结构与算法---二叉树(删除节点)
javascript数据结构与算法---二叉树(删除节点) function Node(data,left,right) { this.data = data; this.left = left; t ...
- javascript数据结构与算法---二叉树(查找最小值、最大值、给定值)
javascript数据结构与算法---二叉树(查找最小值.最大值.给定值) function Node(data,left,right) { this.data = data; this.left ...
- javascript数据结构与算法--二叉树遍历(后序)
javascript数据结构与算法--二叉树遍历(后序) 后序遍历先访问叶子节点,从左子树到右子树,再到根节点. /* *二叉树中,相对较小的值保存在左节点上,较大的值保存在右节点中 * * * */ ...
- javascript数据结构与算法--二叉树遍历(先序)
javascript数据结构与算法--二叉树遍历(先序) 先序遍历先访问根节点, 然后以同样方式访问左子树和右子树 代码如下: /* *二叉树中,相对较小的值保存在左节点上,较大的值保存在右节点中 * ...
- javascript数据结构与算法--二叉树遍历(中序)
javascript数据结构与算法--二叉树遍历(中序) 中序遍历按照节点上的键值,以升序访问BST上的所有节点 代码如下: /* *二叉树中,相对较小的值保存在左节点上,较大的值保存在右节点中 * ...
- javascript数据结构与算法--二叉树(插入节点、生成二叉树)
javascript数据结构与算法-- 插入节点.生成二叉树 二叉树中,相对较小的值保存在左节点上,较大的值保存在右节点中 /* *二叉树中,相对较小的值保存在左节点上,较大的值保存在右节点中 * * ...
- javascript数据结构与算法--散列
一:javascript数据结构与算法--散列 一:什么是哈希表? 哈希表也叫散列表,是根据关键码值(key,value)而直接进行访问的数据结构,它是通过键码值映射到表中一个位置来访问记录的,散列 ...
- 为什么我要放弃javaScript数据结构与算法(第八章)—— 树
之前介绍了一些顺序数据结构,介绍的第一个非顺序数据结构是散列表.本章才会学习另一种非顺序数据结构--树,它对于存储需要快速寻找的数据非常有用. 本章内容 树的相关术语 创建树数据结构 树的遍历 添加和 ...
随机推荐
- Kafka auto.offset.reset
要从头消费kafka的数据,可以通过以下参数: Kafka auto.offset.reset = earliest
- JAVA的初始化顺序
这里主要是介绍JAVA的类的初始化顺序,比较基础:主要是以例子演示为主: 例子一: 1 package com.cnblog.GDUTtiantian; 2 3 /** 4 * 5 * @author ...
- 11.Scrapy登录
Request Request 部分源码: # 部分代码 class Request(object_ref): def __init__(self, url, callback=None, metho ...
- ASP.NET自定义错误页并返回正确的500、404状态码
在项目中,我们常常需要自定义错误页面,但往往返回的状态码都变成了200,对SEO很不友好.我尝试过在百度上寻找解决方案,但找到的资料中说的方法都试过了,发现都是无法返回正确的状态码的. 最后,只好自已 ...
- [实战演练]蜻蜓FM2014年校招笔试题目 - 规则二叉树
题目:某规则二叉树的定义是:对于树中任意两个叶结点A.B,他们与根结点的距离分别是d1和d2,|d1-d2|<=1.请写出函数 bool isRuledTree(Node *root)的代码实现 ...
- 【spring cloud】spring cloud2.X spring boot2.0.4调用feign配置Hystrix Dashboard 和 集成Turbine 【解决:Hystrix仪表盘Unable to connect to Command Metric Stream】【解决:Hystrix仪表盘Loading...】
环境: <java.version>1.8</java.version><spring-boot.version>2.0.4.RELEASE</spring- ...
- flask_maple使用文档
安装 To install Flask-Maple: pip install flask-maple Or alternatively, you can download the repository ...
- [学习笔记]后缀自动机SAM
好抽象啊,早上看了两个多小时才看懂,\(\%\%\%Fading\) 早就懂了 讲解就算了吧--可以去看看其他人的博客 1.[模板]后缀自动机 \(siz\) 为该串出现的次数,\(l\) 为子串长度 ...
- Spring Boot日志管理
SpringBoot内部使用Commons Logging来记录日志,但是默认也提供了对常用日志组件的支持,如:Log4j,Logback等.每种Logger都可以通过配置使用控制台或者文件输出日志内 ...
- 重识 PWA 进阶到 workbox3
看到PWA,似曾相识,但又感觉很模糊,于是乎,又重新翻阅文档,学习了一遍,顺便把相关知识学习了一下,比如service worker,workbox3. PWA 概念: 全称:Progressive ...
