拓展KMP算法详解

　　拓展KMP解决的问题是给两个串S和T，长度分别是n和m，求S的每一个后缀子串与T的最长公共前缀分别是多少，记作extend数组，也就是说extend[i]表示S[i,n-1]（i从0开始）和T的最长公共前缀长度。

　　需要注意的是如果extend[i]=m,即S[i,n-1]和T的最长公共前缀长度是m（正好是T的长度），那么就表示T在S中找到匹配而且起始位置是i，这就解释了为什么这个算法叫做拓展KMP了。

　　其实大致和KMP有异曲同工之妙，都是匹配，都是借用一个next数组。　

　　下面举一个例子，S=”aaaabaa”,T=”aaaaa”,首先，计算extend[0]时，需要进行5次匹配，直到发生失配。

　　

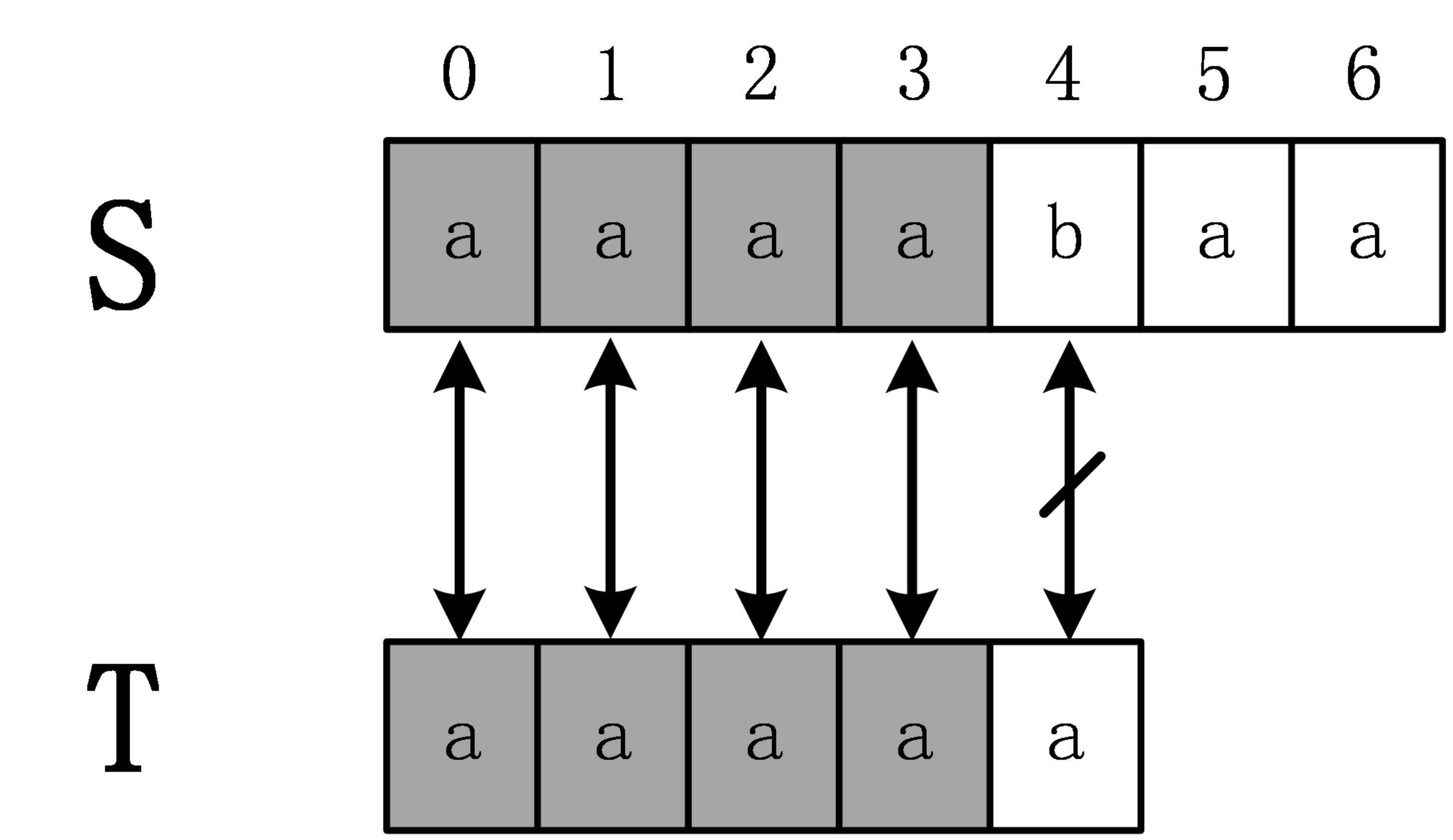
　　从而得知extend[0]=4，下面计算extend[1],在计算extend[1]时，是否还需要像计算extend[0]时从头开始匹配呢？答案是否定的，因为通过计算extend[0]=4，从而可以得出S[0,3]=T[0,3]，进一步可以得到 S[1,3]=T[1,3],计算extend[1]时，事实上是从S[1]开始匹配，设辅助数组next[i]表示T[i,m-1]和T的最长公共前缀长度。在这个例子中，next[1]=4,即T[0,3]=T[1,4],进一步得到T[1,3]=T[0,2],所以S[1,3]=T[0,2],所以在计算extend[1]时，通过extend[0]的计算，已经知道S[1,3]=T[0,2],所以前面3个字符已经不需要匹配，直接匹配S[4]和T[3]即可，这时一次就发生失配，所以extend[1]=3。这个例子很有代表性，有兴趣的读者可以继续计算剩下的extend数组。

1. 拓展kmp算法一般步骤

通过上面的例子，事实上已经体现了拓展kmp算法的思想，下面来描述拓展kmp算法的一般步骤。

　　首先我们从左到右依次计算extend数组，在某一时刻，设extend[0...k]已经计算完毕，并且之前匹配过程中所达到的最远位置为P，所谓最远位置，严格来说就是i+extend[i]-1的最大值（0<=i<=k）,并且设这个最大值的位置为po，如在上一个例子中,计算extend[1]时，P=3，po=0。

现在要计算extend[k+1],根据extend数组的定义，可以推断出S[po,P]=T[0,P-po],从而得到 S[k+1,P]=T[k-po+1,P-po],令len=next[k-po+1]，(回忆下next数组的定义),分两种情况讨论：

第一种情况：k+len<P

如下图所示：

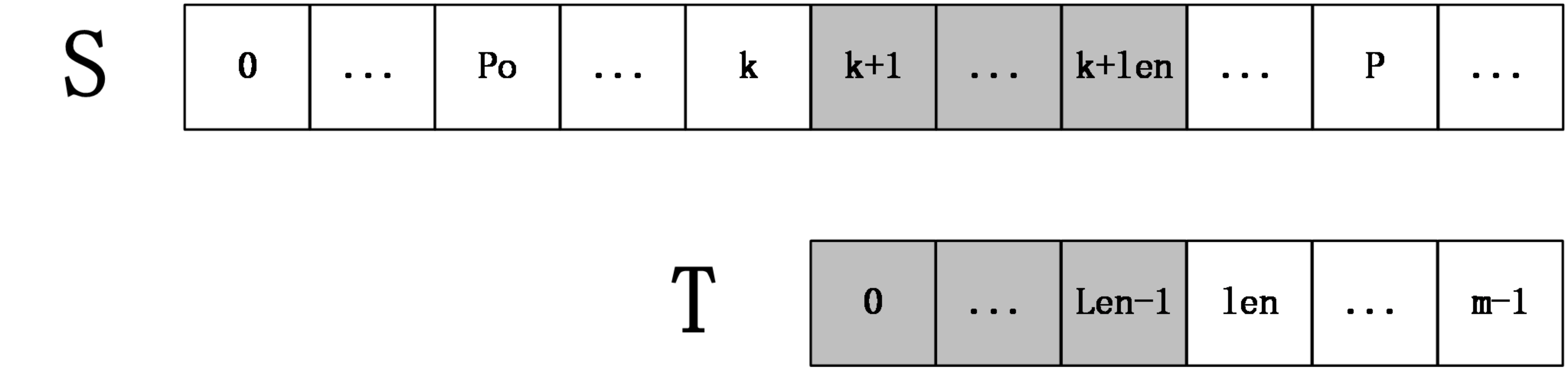
　　上图中，S[k+1,k+len]=T[0,len-1]，然后S[k+len+1]一定不等于T[len]，因为如果它们相等，则有S[k+1,k+len+1]=T[k+po+1,k+po+len+1]=T[0,len],那么next[k+po+1]=len+1，这和next数组的定义不符(next[i]表示T[i,m-1]和T的最长公共前缀长度)，所以在这种情况下，不用进行任何匹配，就知道extend[k+1]=len。

第二种情况： k+len>=P

如下图：

上图中，S[p+1]之后的字符都是未知的，也就是还未进行过匹配的字符串，所以在这种情况下，就要从S[P+1]和T[P-k+1]开始一一匹配，直到发生失配为止，当匹配完成后，如果得到的extend[k+1]+(k+1)大于P则要更新未知P和po。

　　至此，拓展kmp算法的过程已经描述完成，细心地读者可能会发现，next数组是如何计算还没有进行说明，事实上，计算next数组的过程和计算extend[i]的过程完全一样，将它看成是以T为母串，T为字串的特殊的拓展kmp算法匹配就可以了，计算过程中的next数组全是已经计算过的，所以按照上述介绍的算法计算next数组即可，这里不再赘述。

2. 时间复杂度分析

　　下面来分析一下算法的时间复杂度，通过上面的算法介绍可以知道，对于第一种情况，无需做任何匹配即可计算出extend[i]，对于第二种情况，都是从未被匹配的位置开始匹配，匹配过的位置不再匹配，也就是说对于母串的每一个位置，都只匹配了一次，所以算法总体时间复杂度是O(n)的，同时为了计算辅助数组next[i]需要先对字串T进行一次拓展kmp算法处理，所以拓展kmp算法的总体复杂度为O(n+m)的。其中n为母串的长度，m为子串的长度。

3. 模板

 #include<cstdio>
 #include<cstring>
 const int maxn = ;
 char s[maxn]= "aaaabaa", t[maxn] = "aaaaa";
 int nextt[maxn], ls, lt, extend[maxn];

 void get_next();
 void exkmp();

 int main()
 {
     ls = strlen(s);//不要全局和局部乱用
     lt = strlen(t);

     exkmp();
     for(int i = ; i < lt; i++){
         printf("%d ",nextt[i]);
     }
     puts("");

     for(int i = ; i < ls; i++){
         printf("%d ",extend[i]);
     }
     puts("");
     return ;
 } 

 void get_next(){
     nextt[] = lt;

     int k = ;
     while(k < lt && t[k] == t[k - ])
         k++;
     nextt[] = k;

     int po = ;
     for(k = ; k < lt; k++){
         if(nextt[k - po] + k <  nextt[po] + po)
             nextt[k] = nextt[k - po];
         else{
             int j = nextt[po] + po - k;
             if(j < )
                 j=;
             while(j + k < lt && t[j] == t[j + k])
                 j++;

             nextt[k] = j;
             po = k;
         }
     }
 }

 void exkmp(){
     memset(nextt,,sizeof(nextt));
     get_next();

     int k = ;
     while(k < ls && k < lt && s[k] == t[k])
         k++;
     extend[] = k;

     int po=;
     for(k = ; k < ls; k++){
         if(nextt[k - po] + k < extend[po] + po)
             extend[k] = nextt[k - po];
         else{
             int j = extend[po] + po - k;
             if(j < )
                 j = ;
             while(k + j < ls && j < lt && s[k + j] == t[j])
                 j++;

             extend[k] = j;
             po = k;
         }
     }
 }

4. 模板练习题

https://cn.vjudge.net/problem/HDU-3613

练习题参考解答：https://www.cnblogs.com/wenzhixin/p/9355880.html

5.参考博客原文链接：
https://blog.csdn.net/dyx404514/article/details/41831947