NOIP2017 列队——动态开点线段树

Description:

Sylvia 是一个热爱学习的女♂孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有n×m名学生，方阵的行数为 n，列数为 m。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中的学生从 1 到 n×m 编上了号码（参见后面的样例）。即：初始时，第 i 行第 j 列的学生的编号是(i−1)×m+j。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天中，一共发生了 q件这样的离队事件。每一次离队事件可以用数对(x,y)(1≤x≤n,1≤y≤m)描述，表示第 x 行第 y 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：

向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第 x 行第 m 列。
向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第 n 行第 m 列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后，下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 n 行第 m 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后方阵中同学的编号可能是乱序的。

Hint

Solution

一年前暴力敲了30pts

一年后暴力敲了60pts

没什么长进啊

还是不会正解。

1.不懂树状数组

2.不想写平衡树

所以我们写动态开点线段树

首先发现，对于x=1的点，可以想到对这个链开一棵长度为max(n,m)+q的线段树。每次找第k个有数的地方，然后放到最后的位置。

发现，每次向前对齐只有最后一列要动，

向左看齐，只是当前的行会向左移动。

所以，为了便于操作，我们开n+1棵线段树，前n棵维护i行，1~m-1的答案

最后一棵n+1，维护最后一列n个答案。

然后我们就得到了一个优秀的MLE做法辣！~~

所以就要动态开点线段树。

（因为我比较弱）所以简单讲解一下动态开点线段树。

发现，有的时候，线段树需要维护的区间很大很大，但是实际用到的节点很少很少。

那么，我们干脆就不要开这么多的节点，用到的时候再向内存要。

也就是说，我们建立了一棵残疾的线段树，缺少很多枝叶，但是绝对够用了。

画个图大概理解一下（虽然也不太对）

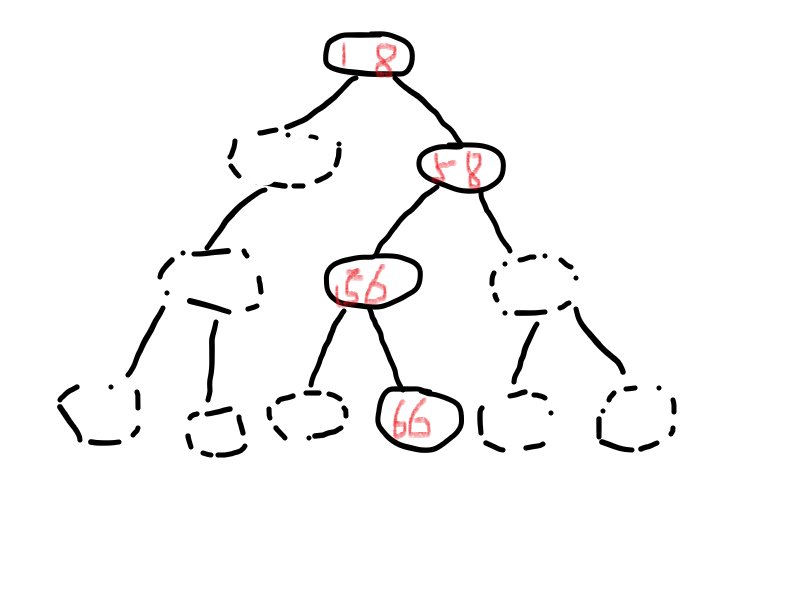
实心边框的点都是我们申请内存给的，虚的点是没用的。就算申请也不用，实在是浪费资源。

所以，

我们开局只有一个根，装备叶子全靠给。

例如我们要建立一个权值线段树，但是在线操作不让你离散化，值域又是inf级别的，

像这样，即使这个区间的范围很大，但是如果询问q比较少的话，我们只需要qloginf个节点，就可以办到。

（发现和主席树有点像，但是省空间的思想还是有些不同的。）

然后我们用动态开点线段树来做这个题。

线段树根节点维护的区间是max(n,m)+q;

开始每个线段树甚至连根也不用建，需要的时候会建起来。

每个线段树节点记录sz，子树实际的人数大小。（开始的时候，只有1~n（m-1）是sz=r-l+1的）

sz可以用一个函数处理。虽然并没有这么多的叶子，但是实际上，建出这么多的叶子，也是这个sz（这也是能动态开点的条件）

再记录一个val（long long型需注意），记录当前节点所代表的人的编号

这个编号val只有在叶子节点才有用。

其实每次询问引起的变化是：树x的第y个人走了，进入了树n+1的末尾，树n+1的第x走了，进入树x的末尾。

每次询问，如果y==m就进入线段树n+1查询，否则进入线段树x查询，找到答案ans输出

查询的时候，顺便sz--，删掉途经点的sz（就不用pushup了）

把ans这个编号放进n+1线段树的末尾（新开一个位置）

同样，途经sz++

如果y！=m说明，第x棵线段树最后进来一个人。就把n+1的第x个人查询（删除），放进线段树x的末尾（新开一个位置）。

这样子，其实每棵线段树根节点的sz都保持为m-1(或n)

Code

#include<bits/stdc++.h>

#define mid ((l+r)>>1)

using namespace std;

typedef long long ll;

const int N=3e5+;

const int M=1e7+;

ll n,m,q;

struct node{

    int ls,rs;

    int sz;

    ll val;

}t[M];

int id,tot;

int rt[N];

ll now;

int cur[N];

int up;

int get(int l,int r){

    if(now==n+){

        if(r<=n) return r-l+;

        if(l<=n) return n-l+;

        return ;

    }

    if(r<m) return r-l+;

    if(l<m) return m-l;

    return ;

}

ll query(int &x,int l,int r,int c){

    if(!x){

        x=++tot;

        t[x].sz=get(l,r);

        if(l==r){

            if(now==n+) t[x].val=l*m;

            else t[x].val=(now-)*m+l;

        }

    }

    t[x].sz--;

    if(l==r) return t[x].val;

    if((!t[x].ls&&c<=get(l,mid))||c<=t[t[x].ls].sz) return query(t[x].ls,l,mid,c);

    else{

        if(!t[x].ls) c-=get(l,mid);

        else c-=t[t[x].ls].sz;

        return query(t[x].rs,mid+,r,c);

    }

}

void upda(int &x,int l,int r,int to,ll d){

    if(!x){

        x=++tot;

        t[x].sz=get(l,r);

        if(l==r){

            t[x].val=d;

        }

    }

    t[x].sz++;

    if(l==r) return;

    if(to<=mid) return upda(t[x].ls,l,mid,to,d);

    else return upda(t[x].rs,mid+,r,to,d);

}

int main()

{

    scanf("%lld%lld%lld",&n,&m,&q);

    int x,y;

    ll ans;

    up=max(n,m)+q;

    while(q--){

        scanf("%d%d",&x,&y);

        if(y==m) now=n+,ans=query(rt[now],,up,x);

        else now=x,ans=query(rt[now],,up,y);

        printf("%lld\n",ans);

        now=n+;

        upda(rt[now],,up,n+(++cur[now]),ans);

        if(y!=m){

            now=n+;

            ans=query(rt[now],,up,x);

            now=x;

            upda(rt[now],,up,m-+(++cur[now]),ans);

        }

    }

    return ;

}

upda：2018.11.2

感觉这个动态开点线段树其实不算是典型的动态开点23333

一般的线段树都是区间表示连续一些下标之类。动态开点也是如此。

但是这个做法的话，愣是把线段树写成了平衡树的存储方式。

区间的长度仅仅代表的是预留空间。

就是把许多点压成了一个点。