POJ.2774.Long Long Message/SPOJ.1811.LCS(后缀自动机)

题目链接 POJ2774

SPOJ1811 LCS - Longest Common Substring

确实比后缀数组快多了(废话→_→)。

\(Description\)

求两个字符串最长公共子串

\(Solution\)

对串A建立后缀自动机。

A的SAM中包含A的所有子串，且根到每个节点的路径都是A的子串。如果B(的一部分?)匹配到了SAM上的某个节点，那么这便是AB的公共子串。求出这些点的max(len)即可。

用串B在SAM上逐位匹配，如果匹配，就继续沿着匹配边走；

否则，为了匹配当前这位，丢掉B前面一部分，因为fa[p]节点代表的后缀是p所代表后缀的上一个可接受后缀，所以跳fa[p]，直到可匹配当前位或到根节点。

注意now的更新方式，如果匹配则+1，否则跳完p后，在p=son[p][c]前用len[p]+1更新now。因为此时p完全匹配了，而len[son[p][c]]是son[p][c]所代表的串的max(len)。(大概是这样吧。。)

感觉这东西好玄学啊。。

//15064K	79MS
//SPOJ:69M	0.04s
#include <cstdio>
#include <cstring>
#include <algorithm>
const int N=250005<<1;//2n

char s[N>>1];
struct Suffix_Automaton
{
	int las,tot,son[N][26],fa[N],len[N];
	void Insert(int c)
	{
		int p=las,np=++tot; len[las=np]=len[p]+1;
		for(; p&&!son[p][c]; p=fa[p]) son[p][c]=np;
		if(!p) fa[np]=1;
		else
		{
			int q=son[p][c];
			if(len[q]==len[p]+1) fa[np]=q;
			else
			{
				int nq=++tot; len[nq]=len[p]+1;
				memcpy(son[nq],son[q],sizeof son[q]);
				fa[nq]=fa[q], fa[q]=fa[np]=nq;
				for(; son[p][c]==q; p=fa[p]) son[p][c]=nq;
			}
		}
	}
	void Build(char *s)
	{
		las=tot=1;
		for(int i=0,l=strlen(s); i<l; ++i) Insert(s[i]-'a');
	}
	void Query(char *s)
	{
		int ans=0;
		for(int c,now=0,p=1,i=0,l=strlen(s); i<l; ++i,ans=std::max(ans,now))
			if(son[p][c=s[i]-'a']) p=son[p][c], ++now;
			else
			{
				for(; p&&!son[p][c]; p=fa[p]);
				if(!p) p=1, now=0;
				else now=len[p]+1, p=son[p][c];
//			WA:	else p=son[p][c], now=len[p];
			}
		printf("%d",ans);
	}
}sam;

int main()
{
	scanf("%s",s), sam.Build(s);
	scanf("%s",s), sam.Query(s);
	return 0;
}

---

一些有关后缀自动机的东西：

论文。。

构造：

后缀自动机详解(感觉这写的理论好理解)

后缀自动机学习小结(从维护right来写？)

后缀自动机学习总结(从简化状态来写？)

后缀自动机构造过程演示(这个过程演示很好啊)

后缀自动机的构造(没看)

题目：

后缀自动机的性质应用

后缀自动机总结

后缀自动机学习小结(应用理论)

几张SAM的例图：

aabbab



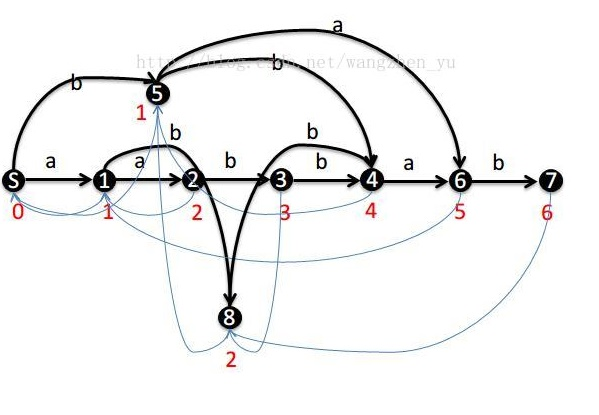
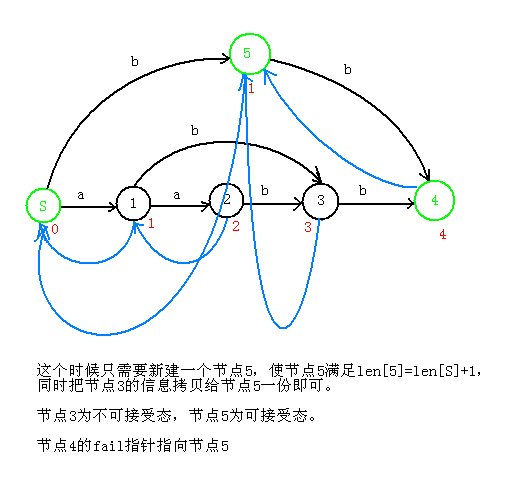
aabb

---