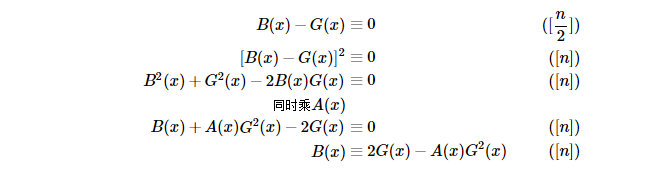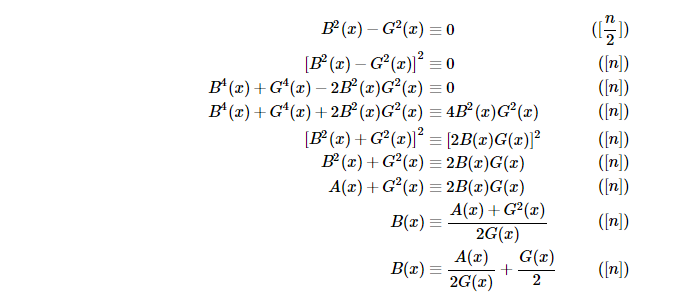【FFT&NTT 总结】

$FFT$总结

（因为还不会啊，，都没做过什么题，所以一边学一边打咯。。

1、主要是用来加速卷积形式的求和吧？

　　$F*G(n)=F[i] × G[n-i]$

　　平时是$O（n^2)$的，FFT可以$O(nlogn)$

2、相当于求两个多项式的乘积（你要求的函数是其系数）

　　$A(x)=A0+A1*x+A2*x^2+A3*x^3+...+An−1*x^{n−1}$

　　$B(x)=B0+B1*x+B2*x^2+B3*x^3+...+Bm−1*x^{m−1}$

3、具体步骤？

　　系数表达->点值表达->相乘->点值表达->系数表达

4、点值表示法

把多项式$A(x)$代入若干个x的值得到若干个点$(x0,A(x0)),(x1,A(x1)),(x2,A(x2)),...,(xn−1,A(xn−1))$

　 我们把从点值表达式转化为系数表达式的操作称为插值

　[点值表示法对应系数表示法是有唯一性的]

5、n次单位复根

　　n次单位复根是满足w^n=1的复数w，有n个。他们均匀分布在以复平面的原点为圆心的单位圆上

　　为$e^{\dfrac{2πki}{n}}$

　　复数幂的定义$e^{ui}=cos(u)+isin(u)$

不如看这里吧

很详细的。

于是略过。

递归式模板

#include<cstdio>
#include<iostream>
#include<cmath>
#include<memory.h>
#define N 400010
using namespace std;
const double pi=acos(-1);

struct P
{
    double x,y;
    P() {x=y=0;}
    P(double x,double y):x(x),y(y){}
}a[N],b[N];

P operator + (P x,P y) {return P(x.x+y.x,x.y+y.y);}
P operator - (P x,P y) {return P(x.x-y.x,x.y-y.y);}
P operator * (P x,P y) {return P(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x);}

void fft(P *s,int n,int t)
{
    if(n==1) return;
    P a0[n>>1],a1[n>>1];
    for(int i=0;i<=n;i+=2) a0[i>>1]=s[i],a1[i>>1]=s[i+1];
    fft(a0,n>>1,t);fft(a1,n>>1,t);
    P wn(cos(2*pi/n),t*sin(2*pi/n)),w(1,0);
    for(int i=0;i<(n>>1);i++,w=w*wn) s[i]=a0[i]+w*a1[i],s[i+(n>>1)]=a0[i]-w*a1[i];
    //w^2=(w+(n>>1))^2 均匀分布在圆上面？
    //w[i^2,n]=w[i/2,n/2] 折半引理
    //s[i]=a0’(i^2)+i*a1’(i^2)=a0(i)+i*a1(i)
    //s[i+n>>1]=a0’((i+n>>1)^2)+i*a1’((i+n>>1)^2)=a0’(i^2)-i*a1’(i^2)
    //因为i=-(i+n>>1) 折半引理
}

int main()
{
    int n,m,nn;
    scanf("%d%d",&n,&m);
    memset(a,0,sizeof(a));memset(b,0,sizeof(b));
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
    nn=1;while (nn<=n+m) nn<<=1;
    fft(a,nn,1);fft(b,nn,1);
    for(int i=0;i<=nn;i++) a[i]=a[i]*b[i];
    fft(a,nn,-1);
    for(int i=0;i<=n+m;i++) printf("%d ",(int)(a[i].x/nn+0.5));
    return 0;
}

　　

迭代式模板

高效实现$FFT$

也就是使用迭代代替递归

比如n=8，R数组长这样：

$a0,a4,a2,a6,a1,a5,a3,a7$

也称作位逆序置换

 

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<complex>
#define Maxn 262145
#define pi acos(-1)
using namespace std;

struct P
{
    double x,y;
    P() {x=y=0;}
    P(double x,double y):x(x),y(y){}
    friend P operator + (P x,P y) {return P(x.x+y.x,x.y+y.y);}
    friend P operator - (P x,P y) {return P(x.x-y.x,x.y-y.y);}
    friend P operator * (P x,P y) {return P(x.x*y.x-x.y*y.y,x.x*y.y+x.y*y.x);}
}a[Maxn],b[Maxn];

int nn;
int R[Maxn];
void fft(P *a,int f)
{
    for(int i=0;i<nn;i++) if(i<R[i]) swap(a[i],a[R[i]]);
    for(int i=1;i<nn;i<<=1)
    {
        P wn(cos(pi/i),f*sin(pi/i));
        for(int j=0;j<nn;j+=i<<1)
        {
            P w(1,0);
            for(int k=0;k<i;k++,w=w*wn)
            {
                P x=a[j+k],y=w*a[j+k+i];
                a[j+k]=x+y;a[j+k+i]=x-y;
            }
        }
    }
}
int main()
{
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i=0;i<=n;i++) scanf("%lf",&a[i].x);
    for(int i=0;i<=m;i++) scanf("%lf",&b[i].x);
    int ll=0;nn=1;
    while(nn<=n+m) ll++,nn<<=1;
    for(int i=0;i<nn;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(ll-1));
    fft(a,1);fft(b,1);
    for(int i=0;i<=nn;i++) a[i]=a[i]*b[i];
    fft(a,-1);
    for(int i=0;i<=n+m;i++) printf("%d ",(int)(a[i].x/nn+0.5));
    return 0;
}

　　

---

$NTT$

简单复习一下原根

　　1、模p下原根g，即g在模p下的阶为$\varphi(p)$

　　2、g的幂构成模p下的缩系。【很有用！

　　3、p有原根当且仅当 p=2，4，质数^a，2*质数^a

　　4、求原根的方法：

　　　　暴力枚举判断，先找出最小的一个。

　　　　判断方法：对$\varphi(p)$质因数分解，假设为$p1^{r1}*p2^{r2}...*pn^{rn}$

　　　　　　　　　有恒有 $g^{\dfrac{\varphi(p)}{pi}}!=1 (Mod P)$成立，则g是p的原根，否则不是。

　　　　假设最小原根是$g$，则当$gcd(d,\varphi(p))==1$时，$g^d$也是模p下的原根。

　　　　即模p下原根个数为$\varphi(\varphi(p))$

对于$NTT$的题目，原根代替了n次单位复根，作用大致相同。只需把一些地方改成Mod之类的就可以。

具体看这里 【这篇写得太好了

当模数不符合要求？

具体实现方式（不完整代码，只放主要部分）

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
#define Maxn 500010
#define LL long long
const int Mod=998244353;
const int G=3;

int nn,R[Maxn],inv;
void ntt(int *s,int f)
{
	for(int i=0;i<nn;i++) if(i<R[i]) swap(s[i],s[R[i]]);
	for(int i=1;i<nn;i<<=1)
	{
		int wn=qpow(G,(Mod-1)/(i<<1));
		for(int j=0;j<nn;j+=(i<<1))
		{
			int w=1;
			for(int k=0;k<i;k++)
			{
				int x=s[j+k],y=1LL*w*s[j+k+i]%Mod;
				s[j+k]=(x+y)%Mod;s[j+k+i]=((x-y)%Mod+Mod)%Mod;
				w=1LL*w*wn%Mod;
			}
		}
	}
	if(f==-1)
	{
		reverse(s+1,s+nn);
		for(int i=0;i<=nn;i++) s[i]=1LL*s[i]*inv%Mod;
	}
}

int main()
{
        ///////////////////////////////
	nn=1;int ll=0;
	while(nn<=2*n) nn<<=1,ll++;
	for(int i=0;i<=nn;i++) R[i]=(R[i>>1]>>1)|((i&1)<<(ll-1));
	inv=qpow(nn,Mod-2);
	ntt(a,1);ntt(b,1);
	for(int i=0;i<=nn;i++) a[i]=1LL*a[i]*b[i]%Mod;
	ntt(a,-1);
        ///////////////////////////////
	return 0;
}

　　

好啦！！！

其实有很多地方是要证明的，但是我都不会 先记住吧。。

---

多项式求逆 + 多项式开根

多项式求逆的代码实现

void get_inv(int *a,int *b,int len)
{
    static int temp[Maxn];
    if(len==1)
    {
        b[0]=qpow(a[0],Mod-2);
        b[1]=0;
        return;
    }
    get_inv(a,b,len>>1);
    memcpy(temp,a,sizeof(int)*len);
    memset(temp+len,0,sizeof(int)*len);
    NTT(temp,len<<1,1),NTT(b,len<<1,1);
    for(int i=0;i<(len<<1);i++)
        b[i]=1LL*b[i]*(2-1LL*temp[i]*b[i]%Mod+Mod)%Mod;
    NTT(b,len<<1,-1);
    memset(b+len,0,sizeof(int)*len);
}

len为当前模数。不断二分。

2017-04-14 15:00:52