C++求图任意两点间的所有路径

基于连通图，邻接矩阵实现的图，非递归实现。

算法思想：

设置两个标志位，①该顶点是否入栈，②与该顶点相邻的顶点是否已经访问。

A 将始点标志位①置1，将其入栈

B 查看栈顶节点V在图中，有没有可以到达、且没有入栈、且没有从这个节点V出发访问过的节点

C 如果有，则将找到的这个节点入栈，这个顶点的标志位①置1，V的对应的此顶点的标志位②置1

D 如果没有，V出栈，并且将与v相邻的全部结点设为未访问，即全部的标志位②置0

E 当栈顶元素为终点时，设置终点没有被访问过，即①置0，打印栈中元素，弹出栈顶节点

F 重复执行B – E,直到栈中元素为空

先举一个例子吧

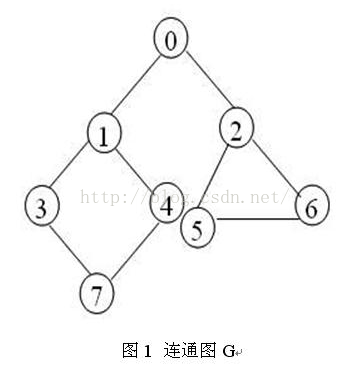
假设简单连通图如图1所示。假设我们要找出结点3到结点6的所有路径，那么，我们就设结点3为起点，结点6为终点。找到结点3到结点6的所有路径步骤如下：
1、 我们建立一个存储结点的栈结构，将起点3入栈，将结点3标记为入栈状态；
2、 从结点3出发，找到结点3的第一个非入栈没有访问过的邻结点1，将结点1标记为入栈状态，并且将3到1标记为已访问；
3、 从结点1出发，找到结点1的第一个非入栈没有访问过的邻结点0，将结点0标记为入栈状态，并且将1到0标记为已访问；
4、 从结点0出发，找到结点0的第一个非入栈没有访问过的邻结点2，将结点2标记为入栈状态，并且将0到2标记为已访问；
5、 从结点2出发，找到结点2的第一个非入栈没有访问过的邻结点5，将结点5标记为入栈状态，并且将2到5标记为已访问；
6、 从结点5出发，找到结点5的第一个非入栈没有访问过的邻结点6，将结点6标记为入栈状态，并且将5到6标记为已访问；
7、 栈顶结点6是终点，那么，我们就找到了一条起点到终点的路径，输出这条路径；
8、 从栈顶弹出结点6，将6标记为非入栈状态；
9、 现在栈顶结点为5，结点5没有非入栈并且非访问的结点，所以从栈顶将结点5弹出，并且将5到6标记为未访问；
10、        现在栈顶结点为2，结点2的相邻节点5已访问，6满足非入栈，非访问，那么我们将结点6入栈；
11、        现在栈顶为结点6，即找到了第二条路径，输出整个栈，即为第二条路径
12、        重复步骤8-11，就可以找到从起点3到终点6的所有路径；
13、        栈为空，算法结束。

下面讲一下C++代码实现

图类，基于邻接矩阵，不详细的写了 ==

 class Graph
 {
 private:
     CArray<DataType,DataType> Vertices;
     int Edge[MaxVertices][MaxVertices];
     int numOfEdges;
 public:
     Graph();
     ~Graph();
     void InsertVertex(DataType Vertex);
     void InsertEdge(int v1,int v2,int weight);
     int GetWeight(int i,int j);
     int GetVertices();
     DataType GetValue(int i);
 }; 

首先自己写一个简单的“栈类”，由于新增了些方法所以不完全叫栈

template<class T>
class Stack
{
private:
    int m_size;
    int m_maxsize;
    T* data;
public:
    Stack();
    ~Stack();
    void push(T data);  //压栈
    T pop(); //出栈，并返回弹出的元素
    T peek(); //查看栈顶元素
    bool isEmpty();  //判断是否空
    int getSize();  //得到栈的中元素个数
    T* getPath();  //返回栈中所有元素
};
template<class T>
Stack<T>::Stack()
{
    m_size=0;
    m_maxsize=100;
    data=new T[m_maxsize];
}
template<class T>
Stack<T>::~Stack()
{
    delete []data;
}
template<class T>
T Stack<T>::pop()
{
    m_size--;
    return data[m_size];
}  
 
template<class T>
void Stack<T>::push(T d)
{
    if (m_size==m_maxsize)
    {
        m_maxsize=2*m_maxsize;
        T* new_data=new T[m_maxsize];
        for (int i=0;i<m_size;i++)
        {
            new_data[i]=data[i];
        }
        delete []data;
        data=new_data;
    }
    data[m_size]=d;
    m_size++;
}  
 
template<class T>
T Stack<T>::peek()
{
    return data[m_size-1];
}  
 
template<class T>
bool Stack<T>::isEmpty()
{
    if (m_size==0)
    {
        return TRUE;
    }
    else
    {
        return FALSE;
    }
}  
 
template<class T>
T* Stack<T>::getPath()
{
    T* path=new T[m_size];
    for (int i=0;i<m_size;i++)
    {
        path[i]=data[i];
    }
    return path;
}  
 
template<class T>
int Stack<T>::getSize()
{
    return m_size;
}

　　Vertex类，便于遍历全部的结点

 class CVertex
 {
 private:
     int m_num;//保存与该顶点相邻的顶点个数
     int *m_nei; //与该顶点相邻的顶点序号
     int *m_flag; //与该顶点相邻的顶点是否访问过
     bool isin; //该顶点是否入栈
 public:
     CVertex();
     void Initialize(int num,int a[]);
     int getOne(); //得到一个与该顶点相邻的顶点
     void resetFlag(); //与该顶点相邻的顶点全被标记为未访问
     void setIsin(bool);//标记该顶点是否入栈
     bool isIn();  //判断该顶点是否入栈
     void Reset();//将isin和所有flag置0
     ~CVertex();  
 
 };  

CVertex::CVertex()
{
    m_num=SIZE;
    m_nei=new int[m_num];
    m_flag=new int[m_num];
    isin=false;
    for (int i=0;i<m_num;i++)
    {
        m_flag[i]=0;
    }  
 
}
void CVertex::Initialize(int num,int a[])
{
    m_num=num;
    for (int i=0;i<m_num;i++)
    {
        m_nei[i]=a[i];
    }
}
CVertex::~CVertex()
{
    delete []m_nei;
    delete []m_flag;
}
int CVertex::getOne()
{
    int i=0;
    for (i=0;i<m_num;i++)
    {
        if (m_flag[i]==0)   //判断是否访问过
        {
            m_flag[i]=1;   //表示这个顶点已经被访问，并将其返回
            return m_nei[i];
        }
    }
    return -1;  //所有顶点都已访问过则返回-1
}
void CVertex::resetFlag()
{
    for (int i=0;i<m_num;i++)
    {
        m_flag[i]=0;
    }
}
void CVertex::setIsin(bool a)
{
    isin=a;
}
bool CVertex::isIn()
{
    return isin;
}
void CVertex::Reset()
{
    for (int i=0;i<m_num;i++)
    {
        m_flag[i]=0;
    }
    isin=false;
}

　　初始化顶点类

int a[SIZE],num;
for ( i=0;i<SIZE;i++)
{
    num=0;
    for (int j=0;j<SIZE;j++)
    {  
 
        if (m_graph.Edge[i][j]!=MaxWeight&&i!=j)
        {
            a[num]=j;
            num++;
        }  
 
    }
    vertex[i].Initialize(num,a);

　　算法实现（由于是基于MFC实现，所有下边的代码不可以直接使用）

stack.push(selection1); //将起点压栈
vertex[selection1].setIsin(true);  //标记为已入栈
int path_num=0;
while (!stack.isEmpty())  //判断栈是否空
{   
 
    int flag=vertex[stack.peek()].getOne();  //得到相邻的顶点
    if (flag==-1)    //如果相邻顶点全部访问过
    {
        int pop=stack.pop(); //栈弹出一个元素
        vertex[pop].resetFlag();  //该顶点相邻的顶点标记为未访问
        vertex[pop].setIsin(false); //该顶点标记为未入栈
        continue; //取栈顶的相邻节点
    }
    if (vertex[flag].isIn())  //若已经在栈中，取下一个顶点
    {
        continue;
    }
    if (stack.getSize()>maxver-1) //判断栈中个数是否超过了用户要求的 ，这里是限制了一条路径节点的最大个数
    {
        int pop=stack.pop();
        vertex[pop].resetFlag();
        vertex[pop].setIsin(false);
        continue;
    }
    stack.push(flag); //将该顶点入栈  
 
    vertex[flag].setIsin(true);  //记为已入栈  
 
    if (stack.peek()==selection2)   //如果栈顶已经为所求，将此路径记录
    {
       int *path=stack.getPath();
           //保存路径的代码省略
       int pop=stack.pop(); //将其弹出，继续探索
           vertex[pop].setIsin(false); //清空入栈的标志位
    }  
 
}