NOIP2002 过河卒（DFS，DP）

https://www.luogu.org/problem/P1002

题目描述

如图，A 点有一个过河卒，需要走到目标 B 点。卒行走规则：可以向下、或者向右。同时在棋盘上的任一点有一个对方的马（如上图的C点），该马所在的点和所有跳跃一步可达的点称为对方马的控制点。例如上图 C 点上的马可以控制 9 个点（图中的P₁，P₂ … P₈ 和 C）。卒不能通过对方马的控制点。

棋盘用坐标表示，A 点（0,0）、B 点（n,m）(n,m 为不超过 20 的整数，并由键盘输入)，同样马的位置坐标是需要给出的（约定: C不等于A，同时C不等于B）。现在要求你计算出卒从 A 点能够到达 B 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。。

输入描述:

输入B点的坐标（n,m）以及对方马的坐标（X,Y）{不用判错}

输出描述:

输出一个整数（路径的条数）。

示例1

输入

输出

说明/提示

结果可能很大！

一开始按DFS做，超时

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <math.h>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const double PI=acos(-);
 const int maxn=;
 using namespace std;
 //ios::sync_with_stdio(false);
 //  cin.tie(NULL);

 int n,m,x,y;
 int ans;

 bool judge(int a,int b)
 {
     if(a==x&&b==y)
         return false;
     if(a==x-&&b==y-)
         return false;
     if(a==x-&&b==y-)
         return false;
     if(a==x+&&b==y-)
         return false;
     if(a==x+&&b==y-)
         return false;
     if(a==x-&&b==y+)
         return false;
     if(a==x+&&b==y+)
         return false;
     if(a==x-&&b==y+)
         return false;
     if(a==x+&&b==y+)
         return false;
     return true;
 }

 void DFS(int a,int b)
 {
     if(a==n&&b==m)
     {
         ans++;
         return ;
     }
     if(a+<=n&&judge(a+,b))
         DFS(a+,b);
     if(b+<=m&&judge(a,b+))
         DFS(a,b+);
 }

 int main()
 {
     scanf("%d %d %d %d",&n,&m,&x,&y);
     DFS(,);
     printf("%d\n",ans);
     return ;
 }

后来以为if判断太多，换了种方法，依然超时

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <math.h>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const double PI=acos(-);
 const int maxn=;
 using namespace std;
 //ios::sync_with_stdio(false);
 //    cin.tie(NULL);

 int n,m,x,y;
 int G[][];
 int ans;

 void DFS(int a,int b)
 {
     if(a==n&&b==m)
     {
         ans++;
         return ;
     }
     if(a+<=n&&G[a+][b]==)
         DFS(a+,b);
     if(b+<=m&&G[a][b+]==)
         DFS(a,b+);
     return ;
 }

 int main()
 {
     //freopen("testdate.in","r",stdin);
     scanf("%d %d %d %d",&n,&m,&x,&y);
     G[x][y]=;
     if(x->=)
     {
         G[x-][y-]=;
         G[x-][y+]=;
     }
     if(y->=)
     {
         G[x-][y-]=;
         G[x+][y-]=;
     }
     if(x->=)
     {
         G[x-][y+]=;
     }
     if(y->=)
     {
         G[x+][y-]=;
     }
     G[x+][y+]=;
     G[x+][y+]=;
     DFS(,);
     printf("%d\n",ans);
     return ;
 }

最后意识到，这题没那么简单.

看过题解才明白这题是记忆化递推，或者说是DP

DP题就是要找到状态转移方程，这题的状态转移方程只用手动模拟一下就可以了，就可以得出到每一个点的方案数就是上面和左边的方案数的总和(因为只可以向右走或向下走)，具体的状态转移方程是

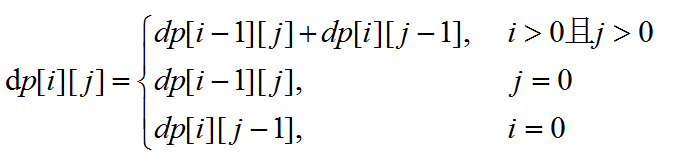
即可以写成DP[i][j]=max(DP[i][j],DP[i-1][j]+DP[i][j-1])

注意，最大的结果已经超过了int的范围，这是一个坑

 #include <stdio.h>
 #include <string.h>
 #include <iostream>
 #include <string>
 #include <math.h>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <set>
 #include <map>
 #include <math.h>
 const int INF=0x3f3f3f3f;
 typedef long long LL;
 const int mod=1e9+;
 const double PI=acos(-);
 const int maxn=;
 using namespace std;
 //ios::sync_with_stdio(false);
 //    cin.tie(NULL);

 int n,m,x,y;
 LL DP[][];//DP[i][j]代表从A点到(i,j)的线路条数
 bool G[][];//判断这个点有没有马盯着
 //马可以走到的位置
 int fx[]={,-,-,,,,,-,-};
 int fy[]={,,,,,-,-,-,-};

 int main()
 {
     scanf("%d %d %d %d",&n,&m,&x,&y);
     n+=;m+=,x+=,y+=;//坐标加2，防止标记马时越界
     for(int i=;i<=;i++)//标记马的位置
     {
         G[x+fx[i]][y+fy[i]]=true;
     }
     DP[][]=;//初始化
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=m;j++)
         {
             if(G[i][j])
                 continue;
             DP[i][j]=max(DP[i][j],DP[i-][j]+DP[i][j-]);//状态转移方程
         }
     }
     printf("%lld\n",DP[n][m]);
     return ;
 }

下面粘一个有意思的代码(递推)：

我们可以发现一个规律：每个数都等于它上面左边的数的和

 #include <iostream>
 using namespace std;

 int n,m,my,mx;
 long long a[][];

 int main()
 {
     cin >>n >>m >>my >>mx;//输入数据
     n=n+;m=m+;my=my+;mx=mx+; //隔出两格，当要把马可跳到的地方掷成0时不会出错
     for(int z=;z<=m;z++)
     {
         for(int y=;y<=n;y++)
         {
             a[z][y]=a[z-][y]+a[z][y-]; //将这个数左边和上面的数相加
             a[][]=;//由于会把起点掷成0，所以要回归1
             a[mx][my]=;//将马的地方掷成0
             a[mx+][my+]=;a[mx+][my-]=;//将马可跳到的地方掷成0
             a[mx-][my+]=;a[mx-][my-]=;//将马可跳到的地方掷成0
             a[mx+][my+]=;a[mx+][my-]=;//将马可跳到的地方掷成0
             a[mx-][my+]=;a[mx-][my-]=;//将马可跳到的地方掷成0
         }
     }
     cout <<a[m][n];//输出结果
     return ;
 }