JavaScript图形实例：图形的平移和对称变换

1.1 六瓣花平移变换

平移变换是指图形从一个位置到另一个位置所作的直线移动。如果要把一个位于P（x,y）的点移到新位置P’(x’,y’)，如图1，则只要在原坐标上加上平移距离Tx和Ty即可。

即 x’=x+Tx

y’=y+Ty

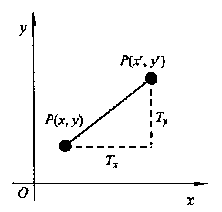
图1 点的平移

生成一个六瓣花型图案的基本数据，通过平移变换绘制8行8列共64个六瓣花型的图案。

编写如下的HTML代码。

<!DOCTYPE html>

<head>

<title>六瓣花平移变换</title>

function draw(id)

{

var canvas=document.getElementById(id);

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,320,320);

context.strokeStyle="blue";

context.lineWidth=1;

var dig=Math.PI/64;

var x=new Array();

var y=new Array();

var r=40;

// 生成一个六瓣花型图案的基本数据

for (var i=0;i<=128;i++)

{

d=r/2*(0.8+Math.sin(18*i*dig)/5)*1.3;

t=d*(0.5+Math.sin(6*i*dig)/2);

x[i]=t*Math.cos(i*dig);

y[i]=t*Math.sin(i*dig);

}

// 通过平移变换绘制8行8列共64个六瓣花型的图案

for (var row=1;row<=8;row++)

for (var col=1;col<=8;col++)

{

// 计算平移量px和py

px=(2*col-1)/2*r;

py=(2*row-1)/2*r;

for (i=0;i<=128;i++)

{

x1=x[i]+px;

y1=y[i]+py;

if (i==0)

{

context.moveTo(x1,y1);

bx=x1; by=y1;

}

else

context.lineTo(x1,y1);

}

context.lineTo(bx,by);

context.closePath();

context.stroke();

}

</script>

</head>

<canvas id="myCanvas" width="320" height="320">您的浏览器不支持canvas！

</canvas>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中绘制出64个六瓣花型的图案，如图2所示。

图2 64个六瓣花型的图案

1.2 对称变换

对称变换的公式如下：

x’=ax+by

y’=cx+dy

当a,b,c,d 取不同值时，产生不同的对称变换。

（1）当b=c=0,a=-1,d=1 时，产生相对于y 轴对称的反射图形。

（2）当b=c=0,a=1,d=-1 时，产生相对于x 轴对称的反射图形。

（3）当b=c=0,a=d=-1 时，产生相对于原点对称的反射图形。

（4）当b=c=1,a=d=0 时，产生相对于直线y=x 对称的反射图形。

（5）当b=c=-1,a=d=0 时，产生相对于直线y=-x 对称的反射图形。

各对称变换如图3所示。

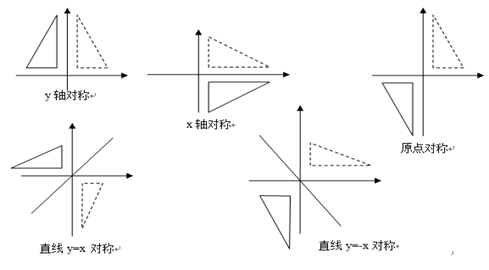
图3 对称变换

在半径为60的圆周上取5个等分点，用这5个点依次首尾连接画5条线，可以绘制出一个正多边形。用这个正多边形为原图，根据选择的方式，进行对称变换。

编写如下的HTML代码。

<!DOCTYPE html>

<head>

// 定义保存基本图案数据的数组

var x=new Array(10);

var y=new Array(10);

var dig=2*Math.PI/5;

for (var i=0;i<=5;i++)

{

x[i]=-75+60*Math.sin(i*dig);

y[i]=-75+60*Math.cos(i*dig);

}

function draw()

{

var sele=document.frm.shape.selectedIndex;

var canvas=document.getElementById("myCanvas");

if (canvas==null)

return false;

var context=canvas.getContext('2d');

context.fillStyle="#EEEEFF";

context.fillRect(0,0,300,300);

//绘制x轴、y轴（注意：我们不进行旋转，故y轴向下）

context.beginPath();

context.moveTo(0,150);

context.lineTo(285,150);

context.moveTo(150,0);

context.lineTo(150,285);

context.strokeStyle = "blue";

context.stroke();

context.fillStyle = "blue";

context.beginPath();

context.moveTo(285,145);

context.lineTo(295,150);

context.lineTo(285,155);

context.closePath();

context.fill();

context.beginPath();

context.moveTo(145,285);

context.lineTo(150,295);

context.lineTo(155,285);

context.closePath();

context.fill();

context.fillStyle="yellow";

context.strokeStyle="red";

context.lineWidth=1;

context.save();

context.translate(150,150);

context.beginPath();

context.moveTo(x[0],y[0]);

for (n=1;n<=5;n++)

{

context.lineTo(x[n],y[n]);

}

context.closePath();

context.stroke();

context.fill();

context.beginPath();

context.moveTo(x[0],y[0]);

context.lineTo(x[2],y[2]);

context.strokeStyle="black";

context.stroke();

context.fillStyle="red";

context.strokeStyle="yellow";

context.beginPath();

switch(sele)

{

case 1: b=c=0,a=1,d=-1; break;

case 2: b=c=0,a=-1,d=1; break;

case 3: b=c=0,a=d=-1; break;

case 4: b=c=1,a=d=0; break;

case 5: b=c=-1,a=d=0; break;

}

context.moveTo(a*x[0]+b*y[0],c*x[0]+d*y[0]);

for (n=1;n<=5;n++)

{

context.lineTo(a*x[n]+b*y[n],c*x[n]+d*y[n]);

}

context.closePath();

context.stroke();

context.fill();

context.beginPath();

context.moveTo(a*x[0]+b*y[0],c*x[0]+d*y[0]);

context.lineTo(a*x[2]+b*y[2],c*x[2]+d*y[2]);

context.strokeStyle="black";

context.stroke();

context.restore();

}

</script>

</head>

<body>

<form name="frm">对称方式选择：

</select>

</form>

<br/>

<canvas id="myCanvas" width="300" height="300">您的浏览器不支持canvas！</canvas>

</body>

</html>

将上述HTML代码保存到一个html文本文件中，再在浏览器中打开包含这段HTML代码的html文件，可以看到在浏览器窗口中，出现“对称方式选择：”下拉列表框，提供5种对称方式的选择，改变选定的对称方式后，可以绘制出基本图案的相应对称变换图案。整个演示过程录屏后展示如图8所示。

图4 图形的对称变换