D. Cow and Snacks 并查集

D. Cow and Snacks

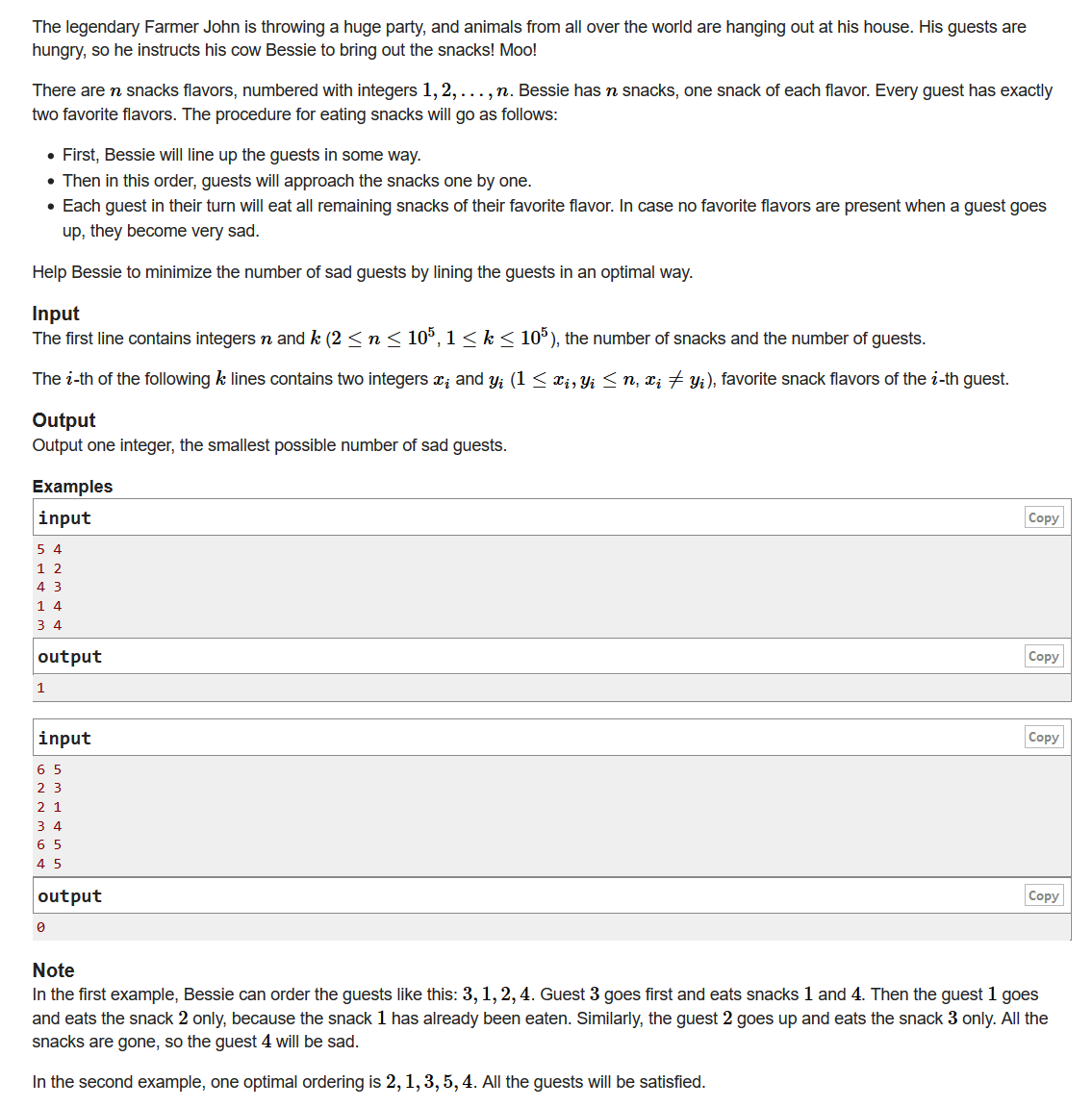
题意：有n种小吃，m个人，每个人有两种喜欢的小吃，当一个人遇到两种自己都喜欢的小吃，可以都吃掉，问在最优的吃小吃顺序下，不能吃到自己喜欢的小吃的人数最少是多少？

题解：把n种小吃当作n个点，m个人当作m条边，每个连通图里面第一个吃的人，一定是可以吃两种自己喜欢的小吃。每次判断这条边是否在已有的联通图里面，对已经在连通图里面的边，是一定不能吃到小吃，若不在连通图里面，则一定可以吃到小吃，用cnt统计可以吃到小吃的人数，最后m-cnt就是答案

#include<iostream>
#include<string.h>
#include<string>
#include<algorithm>
using namespace std;
int p[], r[];
int n,t=;
void init()//初始化集合，每个元素的老板都是自己
{
    for (int i = ; i <= n; i++)
    {
        p[i] = i;
    }
}

int find(int x)//查找元素x的老板是谁
{
    if (x == p[x])
        return x;
    else
        return p[x] = find(p[x]);
}

void join(int x, int y)//合并两个集合
{
    int xRoot = find(x);
    int yRoot = find(y);

    if (xRoot == yRoot) //老板相同，不合并
        return;
    //cnt=cnt-1;
    if (r[xRoot] < r[yRoot]) //r[i]是元素i所在树的高度，矮树的根节点认高树的根节点做老板
        p[xRoot] = yRoot;
    else if (r[xRoot] > r[yRoot])
        p[yRoot] = xRoot;
    else
    {
        p[yRoot] = xRoot;//树高相同，做老板的树高度要加一
        r[xRoot]++;
    }
}

bool sameRoot(int x, int y)//查询两个元素的老板是否相同
{
    return find(x) == find(y);
}
//这里也可以用cnt求不同子集个数，初始化cnt=n,每加入一条边，cnt=cnt-1;
int main()
{
    ios::sync_with_stdio(false);
    int m,cnt=;
    cin>>n>>m;
    init();
    for(int i=;i<m;i++)
    {
        int x,y;
        cin>>x>>y;
        if(!sameRoot(x,y))
        {
            join(x,y);
            cnt++;
        }
    }
    cout<<m-cnt<<endl;
    return ;
}