Java实现 蓝桥杯 历届试题 斐波那契

试题 历届试题 斐波那契

资源限制

时间限制：1.0s 内存限制：256.0MB

问题描述

　　斐波那契数列大家都非常熟悉。它的定义是：

f(x) = 1 … (x=1,2)

　　f(x) = f(x-1) + f(x-2) … (x>2)

对于给定的整数 n 和 m，我们希望求出：

　　f(1) + f(2) + … + f(n) 的值。但这个值可能非常大，所以我们把它对 f(m) 取模。

　　公式如下

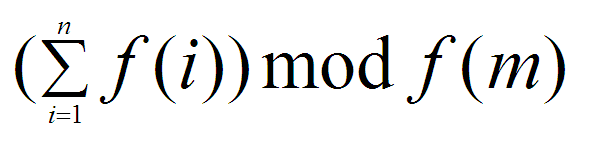
但这个数字依然很大，所以需要再对 p 求模。

输入格式

　　输入为一行用空格分开的整数 n m p (0 < n, m, p < 10^18)

输出格式

　　输出为1个整数，表示答案

样例输入

2 3 5

样例输出

0

样例输入

15 11 29

样例输出

25

import java.math.BigInteger;
import java.util.Scanner;

public class 斐波那契 {
	static BigInteger[][] cal_fm = { { new BigInteger("1"), new BigInteger("1") },
			{ new BigInteger("1"), new BigInteger("0") } };
	static BigInteger[][] cal_sum = { { new BigInteger("2"), new BigInteger("0"), new BigInteger("-1") },
			{ new BigInteger("1"), new BigInteger("0"), new BigInteger("0") },
			{ new BigInteger("0"), new BigInteger("1"), new BigInteger("0") } };
	static BigInteger[][] MOD = { { new BigInteger("1") }, { new BigInteger("1") } };
	static BigInteger[][] SUM = { { new BigInteger("4") }, { new BigInteger("2") }, { new BigInteger("1") } };

	private static BigInteger[][] mult(BigInteger[][] cal_fm2, BigInteger[][] mOD2, BigInteger p, boolean flag) {
		int i_max = cal_fm2.length;
		int j_max = mOD2[0].length;
		int k_max = cal_fm2[0].length;
		if (k_max != mOD2.length) {
			return null;
		}
		BigInteger[][] ans = new BigInteger[i_max][j_max];
		for (int i = 0; i < i_max; i++) {
			for (int j = 0; j < j_max; j++) {
				BigInteger sum = new BigInteger("0");
				for (int k = 0; k < k_max; k++) {
					if (flag) {
						sum = (sum.mod(p)).
								add(cal_fm2[i][k].multiply(mOD2[k][j]).
										mod(p)).
								mod(p);
					} else {
						sum = (sum.add(cal_fm2[i][k].multiply(mOD2[k][j])));
					}
				}
				if (flag) {
					ans[i][j] = sum.mod(p);
				} else {
					ans[i][j] = sum;
				}
			}
		}
		return ans;
	}

	public static String fib(long n, long m, long p) {
		BigInteger mod = new BigInteger("0");
		BigInteger sum = new BigInteger("0");
		if (m > n + 2) {
			if (n == 1) {
				sum = new BigInteger("1");
			} else {
				n = n - 1;
				while (n != 0) {
//					System.out.println(n);
					if ((n & 1) == 1) {
						SUM = mult(cal_sum, SUM, new BigInteger(String.valueOf(p)), true);
					}
					n = n >> 1;
					cal_sum = mult(cal_sum, cal_sum, new BigInteger(String.valueOf(p)), true);
				}
				sum = SUM[2][0];
			}
//			System.out.println(sum);
			return sum.mod(new BigInteger(String.valueOf(p))).toString();
		} else {
			if (m == 1 || m == 2) {
				mod = new BigInteger("1");
			} else {
				m = m - 1;
				while (m != 0) {
					if ((m & 1) == 1) {
						MOD = mult(cal_fm, MOD, new BigInteger(String.valueOf(p)), false);
					}
					m = m >> 1;
					cal_fm = mult(cal_fm, cal_fm, new BigInteger(String.valueOf(p)), false);
				}
				mod = MOD[1][0];
			}
			if (n == 1) {
				sum = new BigInteger("1");
			} else {
				n = n - 1;
				while (n != 0) {
					if ((n & 1) == 1) {
						SUM = mult(cal_sum, SUM, mod, true);
					}
					n = n >> 1;
					cal_sum = mult(cal_sum, cal_sum, mod, true);
				}
				sum = SUM[2][0];
			}
			return sum.mod(new BigInteger(String.valueOf(p))).toString();
		}
	}

	public static void main(String[] args) {
		long n, m, p;
		Scanner scanner = new Scanner(System.in);
		n = scanner.nextLong();
		m = scanner.nextLong();
		p = scanner.nextLong();
		System.out.println(fib(n, m, p));
	}
}