应用统计学

方差分析的基本假设：

组间组平均与总平均的不同是由treatment引发的。单个值与组平均的不同是由组内error引发的。

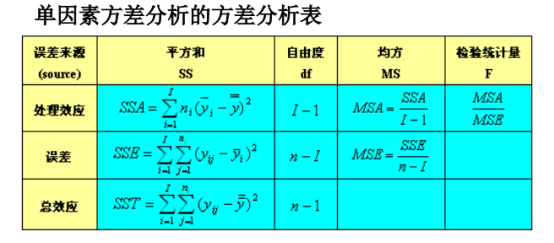
如果没有处理误差SSA=SSE，所以右尾假设如果F>1则处理效应更强

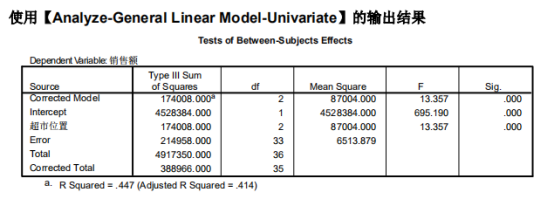
本质上样本方差，所以是总体方差的无偏估计。

描述强度：

增加n（维度），R变大，adjusted R变大。但是n过大就会出现过拟合的现象，此时R虽然变大，但是并不好，并不能反映客观情况，客观情况是变量间差异是本身就很大，而不是因为维度升高导致的。

双因子方差分析除了增加一个因素之外还有两个因素之间的交互作用。

双因子方差分析|adjusted R|强度|SSA|SSE|SST|的更多相关文章

  1. 【数据分析 R语言实战】学习笔记 第八章 方差分析与R实现

    方差分析泛应用于商业.经济.医学.农业等诸多领域的数量分析研究中.例如商业广告宣传方面,广告效果可能会受广告式.地区规模.播放时段.播放频率等多个因素的影响,通过方差分析研究众多因素中,哪些是主要的以 ...

  2. 强制禁用gitlab的双因子认证：Two-Factor Authentication

    (一)问题描述: 此博客解决如下问题:禁用gitlab的双因子认证 禁用前,如图(此时,你在gitlab中什么也干不了) (二)思路分析: 百度了很多方法,都不可靠(如不可靠的说明:https://s ...

  3. （诊断）解决GitHub使用双因子身份认证“Two-Factor Athentication”后无法git push 代码的“fatal: Authentication failed for ...”错误

    在GitHub上采取双因子身份认证后,在git push 的时候将会要求填写用户的用户名和密码,用户名就是用户在GitHub上申请的用户名,但是密码不是普通登录GitHub的密码. 一旦采取双因子身份 ...

  4. odoo12之应用：一、双因子验证(Two-factor authentication, 2FA)（HOTP，TOTP）附源码

    前言 双因子认证:双因子认证(2FA)是指结合密码以及实物(信用卡.SMS手机.令牌或指纹等生物标志)两种条件对用户进行认证的方法.--百度百科 跟我一样"老"的网瘾少年想必一定见 ...

  5. 多因素线性回归|adjusted R^2|膨胀系数|非线性回归|Second-order model with 1 independent variable|Interaction model with 2 independent variables|偏相关|fraction[a]|contribution

    多因素线性回归 系数由最小二乘法得到 R^2;adjusted R^2:变量变多之后,r^2自然变大,但是这不是反应客观事实,所以引入了adjusted R^2 使用散点图看独立性,也可以使用软件,c ...

  6. 实验的方差分析（R语言）

    实验设计与数据处理(大数据分析B中也用到F分布,故总结一下,加深印象)第3课小结--实验的方差分析(one-way analysis of variance) 概述 实验结果\(S\)受多个因素\(A ...

  7. centos6.5使用Google auth进行双因子认证

    1.环境 系统:centos6.5 x86_64 [root@uu ~]# uname -a Linux uu 2.6.32-642.el6.x86_64 #1 SMP Wed Apr 13 00:5 ...

  8. 方差分析|残差|MSA/MSE|Completely randomized design|Randomized block design|LSD|主效应|intercept|多重比较|

    符合方差分析的三个条件: 残差=实际值-预测值(其实是均值). 在原假设下,MSA的期望会等于MSE的期望:在备选假设下,MSA的期望会大于MSE的期望,所以MSA/MSE的取值范围在(1,正无穷), ...

  9. 用Python学分析 - 单因素方差分析

    单因素方差分析(One-Way Analysis of Variance) 判断控制变量是否对观测变量产生了显著影响 分析步骤 1. 建立检验假设 - H0:不同因子水平间的均值无差异 - H1:不同 ...

随机推荐

  1. 实战Arch Unit

    在以前的文章中介绍了通过 [<实战PMD>](https://zhuanlan.zhihu.com/p/105585075).[<实战Checkstyle>](https:// ...

  2. linux messages日志出现kernel: nf_conntrack: table full, dropping packet

    上述结果会让业务访问很慢!各种网络服务耗时大幅上升,各种time out,各种丢包,完全无法正常提供服务,大并发业务场景下,开防火墙很容易出现这种问题. 解决方法1:关闭分防火墙服务 解决方法2:修改 ...

  3. 吴裕雄--天生自然 JAVASCRIPT开发学习：HTML DOM 节点列表

    <!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title> ...

  4. 吴裕雄--天生自然 JAVASCRIPT开发学习：函数参数

    <!DOCTYPE html> <html> <head> <meta charset="utf-8"> <title> ...

  5. Redis_大保健

    Redis redis命令参考网址: http://doc.redisfans.com/ redis主从: 集群:一组通过网络连接的计算机,共同对外提供服务,像一个独立的服务器. 一.简介 nosql ...

  6. MyBatis从入门到精通(第2章)：MyBatis XML方式的基本用法【insert用法、update用法、delete用法】

    2.4  insert 用法 2.4.1  简单的 insert方法 在接口 UserMapper.java 中添加如下方法. /** * 新增用户 * @param sysUser * @retur ...

  7. ubuntu18.04国内软件源

    ubuntu默认的软件源是国外的,下载软件很慢,需要更新为国内的源以提升速度,现在可以通过ubunt software来设置了,不过还是习惯了命令行修改的方式. 更新方法 123 sudo vi /e ...

  8. 零相关|回归|相关|相关系数|回归解释相关|r判断相关性|相关系数的区间估计|数据类型|非线性回归

    零相关是什么? 零相关亦称“不相关”.相关的一种.两个变量的相关系数r=0时的相关.零相关表示两个变量非线性相关,这时两个变量可能相互独立,也可能曲线相关.对于正态变量,两个变量零相关与两个变量相互独 ...

  9. MySql索引机制

    第一部分 MySQL数据库索引的数据结构及算法理论 第二部分 MySQL索引实现机制 第三部分 MySQL中高性能使用索引的策略 数据结构及算法 MySQL官方对索引的定义为:索引(Index)是帮助 ...

  10. 网站的ssl证书即将过期，需要续费证书并更新

    SSL这个证书的续费也挺奇怪,续费跟新购买一样. 证书这个东西,申请成功之后,每次都要重新下载,需要处理好格式之后,放在服务器的指定目录里. 大致操作如下: 首先,申请/续费证书,证书下来后,下载下来 ...