FarmCraft

题意：mhy住在一棵有n个点的树的1号结点上，每个结点上都有一个妹子。mhy从自己家出发，去给每一个妹子都送一台电脑，每个妹子拿到电脑后就会开始安装zhx牌杀毒软件，第i个妹子安装时间为ci。树上的每条边mhy能且仅能走两次，每次耗费1单位时间。mhy送完所有电脑后会回自己家里然后开始装zhx牌杀毒软件。卸货和装电脑是不需要时间的。求所有妹子和mhy都装好zhx牌杀毒软件的最短时间。

分析：不难想到使用树形dp，因为最短时间显然由最后安装完电脑的妹子决定，所以dp[i]表示i所有子树中最后安装完电脑的妹子所需的最短时间，那么如何规定访问的顺序呢？考虑如果该节点所有的儿子均为叶子节点，那么对于x任意两个子节点y，z，显然dp[x]是先走y与先走z中决策的最小值，即dp[x]=min(max(cy+1,cz+3),max(cy+3,cz+1))若cy>cz,则dp[x]=min(max(cy+1,cz+3),cy+3)因为cy+3显然是这几项里的最大值，所以dp[x]=max(cy+1,cz+3)所以也就说明了要先走y再走z顺序，也就是将所有儿子从大到小排序并从最大的开始按照顺序选择，那么推广到一般情况呢，还是对于任意x的任意两个子节点y,z，dp[x]当然也是先走y与先走z中决策的最小值，如果先走y再走z，那么首先你要花1的时间从x到达y，然后再讲y点看成一个修电脑时间为dp[y]的妹子，那么总时间就是dp[y]+1，然后再走z，这个时候根据题目要求你应该已经走完了y子树中所有的节点，而因为只有走边需要花费时间，所以子节点（包括本身）为num[y]个的y子树应该有num[y]-1条边，再加上从x到y的那一条边就一共有num[y]条边，而这些边每条边需要走两遍，最后再回到x节点，所以总花费就是num[y]*2的时间，然后再从x走到z最终是花费dp[z]+num[y]*2+1的时间，而该种走法的最终时间就是max(dp[y]+1,dp[z]+num[y]*2+1),而另一种走法也同理，最终时间是max(dp[z]+1,dp[y]+num[z]*2+1)，dp[x]也就等于这两种走法中的最小值，观察这两个式子dp[z]+num[y]*2+1一定是比dp[z]+1大的，如果dp[z]+num[y]*2+1还比dp[y]+num[z]*2+1大的话显然就一定选择第二种，也就是说dp[z]+num[y]*2+1与dp[y]+num[z]*2+1这两项的大小关系直接影响到我们选择的顺序，而且如果dp[z]+num[y]*2+1>dp[y]+num[z]*2+1的话就选第二种（先走z），否则就选第一种（先走y），稍微化简一下就能得到如果dp[z]-num[z]*2]>dp[y]-num[y]*2的话就先走z，否则先走y，所以要讲x的子节点按照dp[i]-num[i]*2排序，再从大到小选择

最后的走法就是到达这个点之后先让他把这个点的电脑修一下，毕竟不修白不修，然后开始按照上述选择子节点的顺序选择子节点，该点的dp[x]值就是该种走法下每个子节点所需时间与cx的最大值，要注意的是这里的每个子节点所需时间与dp[i]不同，这个地方表示的所需时间是包括了之前走别的地方所花费的时间，具体来说如果这个节点是最后走的，那他应该加上前面所有需要走的边数*2+1（+1为x到这个节点的时间。还有一个很关键的问题，区别好等待时间与实际的时间，比如可能会有个问题，x节点的最后一个子节点与x连的这条边好像返回没有被记录，实际上不需要记录这条边所产生的时间，因为dp[x]表示的是安装完电脑所需的最短时间而不是回到初始点所花费的时间，如果你在未回到起始的1号点时就已经把别的电脑都修完了，那么你所用的时间只是所有边的花费*2+c1，具体可以看看这组数据来感受一下，也就是说最终的结果其实是max(dp[1],(n-1)*2+c1) 其中n-1表示这个树的总边数。

4

1 1 1 1

1 2

2 3

3 4

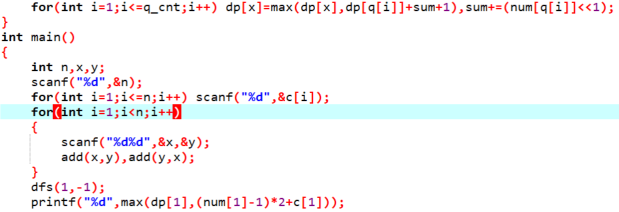
代码：