蝙蝠算法(BA)学习笔记
算法原理
蝙蝠能够在夜间或十分昏暗的环境中自由飞翔和准确无误地捕捉食物,是因为他们能够从喉头发出地超声脉冲回声来定位。受这一启发,Yang教授在2010年提出了蝙蝠算法(Bat Algorithm,BA)[1]。
在蝙蝠算法中,为了模拟蝙蝠捕食猎物、避免障碍地随机搜索过程,做出如下三个近似理想化规则假设[2]:
(1) 种群中所有蝙蝠都利用回声定位的方法感知距离。
(2) 蝙蝠在位置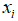 以速度
以速度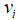 随机飞行,具有固定的频率
随机飞行,具有固定的频率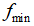 ,同时具有根据自身与猎物距离自动调整的波长
,同时具有根据自身与猎物距离自动调整的波长 和脉冲响度A。
和脉冲响度A。
(3) 假设脉冲响度的变化方式为从一个最大值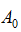 整数变化到固定最小值
整数变化到固定最小值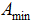 ,变化区间可根据问题调整。
,变化区间可根据问题调整。
假设蝙蝠搜索空间为D维,每一代中蝙蝠位置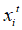 和速度
和速度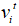 的更新规则如公式(1)~(3)所示。其中
的更新规则如公式(1)~(3)所示。其中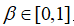 为一个随机变量。
为一个随机变量。 是群体当前局部最优解位置。
是群体当前局部最优解位置。
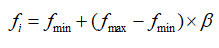 (1)
(1)
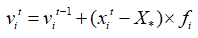 (2)
(2)
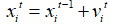 (3)
(3)
而局部搜索时,新的局部解使用随机游走方式生成,如公式(4)。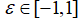 是一个随机数;
是一个随机数;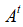 整个群体在同一代中的平均响度。在搜索过程中,蝙蝠会根据距离目标猎物的方位不断减小响度到一个定值的同时不断增大频度,将猎物范围缩小并捕食,在这一过程中,每只蝙蝠的声波响度和频度更新公式如(5)和(6)所示,其中
整个群体在同一代中的平均响度。在搜索过程中,蝙蝠会根据距离目标猎物的方位不断减小响度到一个定值的同时不断增大频度,将猎物范围缩小并捕食,在这一过程中,每只蝙蝠的声波响度和频度更新公式如(5)和(6)所示,其中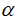 是声波响度衰减系数,值落在0到1之间不包含0和1;
是声波响度衰减系数,值落在0到1之间不包含0和1;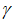 是脉冲频度增强系数大于0;
是脉冲频度增强系数大于0;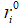 表示为蝙蝠
表示为蝙蝠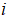 初始脉冲频率。
初始脉冲频率。
 (4)
(4)
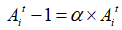 (5)
(5)
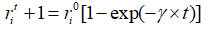 (6)
(6)
蝙蝠算法的基本步骤为:
(1) 参数初始化:蝙蝠种群数量m,迭代次数N,目标函数f(x),蝙蝠位置 ,速度
,速度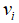 和声波频率
和声波频率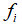 ,声波响度
,声波响度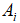 和频度
和频度 。
。
(2) 找出当前种群的最优位置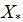 ,根据公式(2)~(4)更新位置和速度。
,根据公式(2)~(4)更新位置和速度。
(3) 生成[0,1]上的随机数rand1,如果rand1>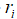 ,在最佳个体(解集)中选择一个最优个体(解),在选择的最优个体(解)周围根据公式(4)生成一个局部个体(解),否则根据公式(4)更新蝙蝠个体位置。
,在最佳个体(解集)中选择一个最优个体(解),在选择的最优个体(解)周围根据公式(4)生成一个局部个体(解),否则根据公式(4)更新蝙蝠个体位置。
(4) 生成[0,1]上的随机数rand2,如果rand2<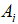 并且
并且 ,则接受该位置,根据公式(6)(7)减小
,则接受该位置,根据公式(6)(7)减小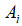 和增大
和增大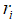 。
。
(5) 对该种群中所有个体适应度值进行排序,并找出当前最佳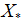 。
。
(6) 重复步骤(2)~(5),判断是否满足最大迭代次数,输出全局最优值。
参考文献
[1] X. S. Yang, A New Metaheuristic Bat-Inspired Algorithm, in: Nature Inspired Cooperative Strategies for Optimization (NISCO 2010), Studies in Computational Intelligence, Springer Berlin, 284, Springer, 65-74 (2010). http://arxiv.org/abs/1004.4170
[2] XU Degang, ZHAO Ping. Literature Survey on Research and Application of Bat Algorithm. CEA, 2019, 55(15): 1-12.
参考代码
1.https://www.mathworks.com/matlabcentral/fileexchange/44707-binary-bat-algorithm
蝙蝠算法(BA)学习笔记的更多相关文章
- 串的应用与kmp算法讲解--学习笔记
串的应用与kmp算法讲解 1. 写作目的 平时学习总结的学习笔记,方便自己理解加深印象.同时希望可以帮到正在学习这方面知识的同学,可以相互学习.新手上路请多关照,如果问题还请不吝赐教. 2. 串的逻辑 ...
- BZOJ 2120 数颜色&2453 维护队列 [带修改的莫队算法]【学习笔记】
2120: 数颜色 Time Limit: 6 Sec Memory Limit: 259 MBSubmit: 3665 Solved: 1422[Submit][Status][Discuss] ...
- BZOJ 2038: [2009国家集训队]小Z的袜子(hose) [莫队算法]【学习笔记】
2038: [2009国家集训队]小Z的袜子(hose) Time Limit: 20 Sec Memory Limit: 259 MBSubmit: 7687 Solved: 3516[Subm ...
- C4.5算法的学习笔记
有日子没写博客了,这些天忙着一些杂七杂八的事情,直到某天,老师喊我好好把数据挖掘的算法搞一搞!于是便由再次埋头看起算法来!说起数据挖掘的算法,我想首先不得的不提起的就是大名鼎鼎的由决策树算法演化而来的 ...
- PAT算法题学习笔记
1001. 害死人不偿命的(3n+1)猜想 (15) 卡拉兹(Callatz)猜想: 对任何一个自然数n,如果它是偶数,那么把它砍掉一半:如果它是奇数,那么把(3n+1)砍掉一半.这样一直反复砍下去, ...
- 「Manacher算法」学习笔记
觉得这篇文章写得特别劲,插图非常便于理解. 目的:求字符串中的最长回文子串. 算法思想 考虑维护一个数组$r[i]$代表回文半径.回文半径的定义为:对于一个以$i$为回文中心的奇数回文子串,设其为闭区 ...
- 算法图解学习笔记01:二分查找&大O表示法
二分查找 二分查找又称折半查找,其输入的必须是有序的元素列表.二分查找的基本思想是将n个元素分成大致相等的两部分,取a[n/2]与x做比较,如果x=a[n/2],则找到x,算法中止:如果x<a[ ...
- vector刘汝佳算法入门学习笔记
//*****-*-----vector***/////// 常用操作封装,a.size();可以读取大小 a.resize();可以改变大小: ...
- 算法导论学习笔记1---排序算法(平台:gcc 4.6.7)
平台:Ubuntu 12.04/gcc 4.6.7 插入排序 #include<vector> #include <algorithm> #include<iostrea ...
随机推荐
- 03 . Python入门之运算符
一.什么是运算符? 举个简单的例子** 4 +5 = 9 . 例子中,4** 和 5 被称为操作数,"+" 称为运算符. Python语言支持以下类型的运算符: [算术运算符] [ ...
- 资源在windows编程中的应用----菜单
资源在Windows编程中的应用 资源 加速键.位图.光标.对话框.菜单.字符串.工具条 1.菜单的创建 菜单由以下组成部分: (1)窗口主菜单条 (2)下拉式菜单框 (3)菜单项热键标识 (4)菜单 ...
- 数字电路建模 - jchdl
https://mp.weixin.qq.com/s/uWU6i30_q7wJT3yVJ8yqnQ jchdl:Jianchang Constructed Hardware Description ...
- 数据库之 MySQL --- 数据处理 之 子查询 (二)
个人博客网:https://wushaopei.github.io/ (你想要这里多有) 一 .数据库语言定义及命令行查看数据库操作 -- SQL 语言可以分为三类-- DML: 数据操纵语言. ...
- Java实现 LeetCode 559 N叉树的最大深度(遍历树,其实和便利二叉树一样,代码简短(●ˇ∀ˇ●))
559. N叉树的最大深度 给定一个 N 叉树,找到其最大深度. 最大深度是指从根节点到最远叶子节点的最长路径上的节点总数. 例如,给定一个 3叉树 : 我们应返回其最大深度,3. 说明: 树的深度不 ...
- java实现纵横火柴棋
[编程题] 这是一个纵横火柴棒游戏.如图[1.jpg],在一个3x4的方格中,游戏的双方轮流放置火柴棒.其规则是: 1. 不能放置在已经放置火柴棒的地方(即只能在空格中放置). 2. 火柴棒的方向只能 ...
- Java实现第九届蓝桥杯哪天返回
哪天返回 题目描述 小明被不明势力劫持.后被扔到x星站再无问津.小明得知每天都有飞船飞往地球,但需要108元的船票,而他却身无分文. 他决定在x星战打工.好心的老板答应包食宿,第1天给他1元钱. 并且 ...
- FTP配置多用户多目录多权限
环境介绍 根据开发的需求 要求创建FTP服务器,把前端和后端分开用不同的FTP账号 系统环境 centos 7.4 selinux 关闭 防火墙关闭 安装FTP 很简单就一条命令 yum instal ...
- 遇到Error:Execution failed for task ':app:transformClassesWithDexForDebug'的解决方案
原因:项目中包含了所有的google play service 解决:只需要使用必要的服务即可 将compile 'com.google.android.gms:play-services:8.1.0 ...
- java第三阶段作业总结
Java第三阶段总结 前言 到这里,Java课程学习进入了尾声,在这学习过程中,我学习到很多,也发现了自己的很多不足,这篇博客主要针对的是Java整门课程学习的总结. 课程收获 对整门课程的学习,我有 ...
