使用CORDIC算法求解角度正余弦及Verilog实现

本文是用于记录在了解和学习CORDIC算法期间的收获，以供日后自己及他人参考；并且附上了使用Verilog实现CORDIC算法求解角度的正弦和余弦的代码、简单的testbench测试代码、以及在Modelsim下的仿真结果。

本文主要参考了：

【1】https://www.cnblogs.com/aikimi7/p/3929592.html （cordic算法的verilog实现及modelsim仿真）

【2】https://www.cnblogs.com/qiweiwang/archive/2010/07/28/1787021.html（CORDIC算法--流水线结构）

【3】https://www.cnblogs.com/yuphone/archive/2010/09/21/1832217.html（[文档].艾米电子 - 算术运算电路，Verilog）

【4】https://wenku.baidu.com/view/54b251aaa98271fe900ef97e（如何理解CORDIC算法）

【5】https://wenku.baidu.com/view/60a0a07831b765ce050814b7（针对正弦余弦计算的CORDIC算法优化及其FPGA实现）

感谢！

-------------------------------------------------------------------------------------------------------------

1、算法简介

CORDIC（Coordinate Rotation Digital Computer）算法即坐标旋转数字计算方法，是J.D.Volder1于1959年首次提出，主要用于三角函数、双曲线、指数、对数的计算。该算法通过基本的加和移位运算代替乘法运算，使得矢量的旋转和定向的计算不再需要三角函数、乘法、开方、反三角、指数等函数，计算向量长度并能把直角坐标系转换为极坐标系。因为Cordic 算法只用了移位和加法，很容易用纯硬件来实现，非常适合FPGA实现。

CORDIC算法是天平称重思想在数值运算领域的杰出范例。核心的思想是把非线性的问题变成了线性的迭代问题【4】。

CORDIC算法完成坐标或向量的平面旋转（下图以逆时针旋转为例）。

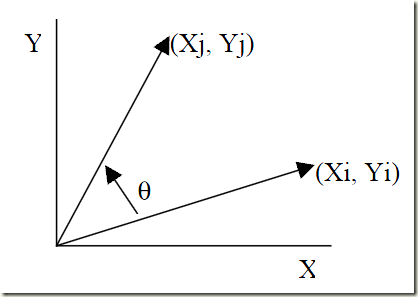
旋转后，可得如下向量：

旋转的角度θ经过多次旋转得到的（步步逼近，接近二分查找法），每次旋转一小角度。单步旋转定义如下公式：

公式（2）提取cosθ，可修改为：

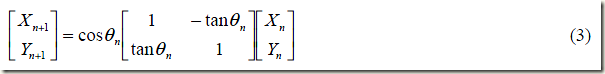
修改后的公式把乘法次数从4次改为3次，剩下的乘法运算可以通过选择每次旋转的角度去除，将每一步的正切值选为2的指数（二分查找法），除以2的指数可以通过右移操作完成（verilog）。

每次旋转的角度可以表示为：

所有迭代角度累加值等于最终需要的旋转角度θ：

这里Sn为1或者-1，根据旋转方向确定（后面有确定方法，公式（15）），顺时针为-1，逆时针为1。

可以得到如下公式：

结合公式（3）和（7），得到公式（8）：

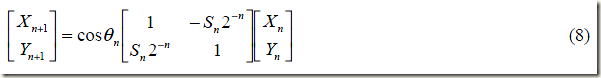
到这里，除了余弦值这个系数，算法只要通过简单的移位和加法操作完成。而这个系数可以通过预先计算最终值消掉。首先重新重写这个系数如下：

第二步计算所有的余弦值并相乘，这个值K称为增益系数。

由于K值是常量，我们可以先忽略它。

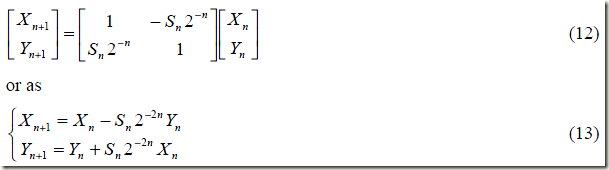
到这里我们发现，算法只剩下移位和加减法，这就非常适合硬件实现了，为硬件快速计算三角函数提供了一种新的算法。在进行迭代运算时，需要引入一个新的变量Z，表示需要旋转的角度θ中还没有旋转的角度。

这里，我们可以把前面提到确定旋转方向的方法介绍了，就是通过这个变量Z的符号确定。

通过公式（5）和（15），将未旋转的角度变为0。

一个类编程风格的结构如下，反正切值是预先计算好的。

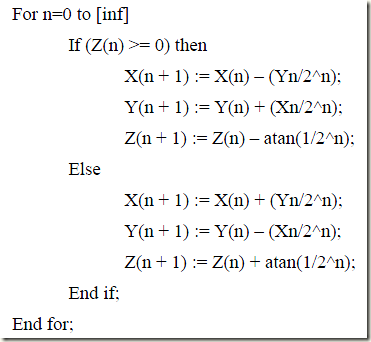
1.1 旋转模式

旋转模式下，CORDIC算法驱动Z变为0，结合公式（13）和（16），算法的核心计算如下：

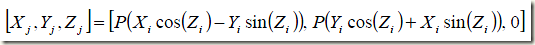
一种特殊情况是，另初始值如下：

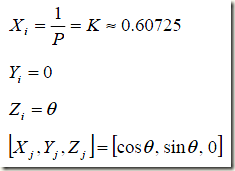
因此，旋转模式下CORDIC算法可以计算一个输入角度的正弦值和余弦值。

1.2 向量模式

向量模式下，有两种特例：

因此，向量模式下CORDIC算法可以用来计算输入向量的模和反正切，也能开方计算，并可以将直角坐标转换为极坐标。

算法介绍：http://en.wikipedia.org/wiki/Cordic，http://blog.csdn.net/liyuanbhu/article/details/8458769

2、硬件算法实现

根据【5】，可以看到CORDIC迭代算法的一种直接实现方式是反馈结构，此结构只设计一级CORDIC运算迭代单元、然后在系统时钟的驱动下，将本级的输出作为本级的输入，通过同一级迭代完成运算。这种方法硬件开销小、但控制相对复杂。

所以根据【1】、【2】，使用流水线结构实现了CORDIC迭代算法、求取了角度的正弦和余弦值。

下面分段介绍下各部分代码：

首先是角度的表示，进行了宏定义，360读用16位二进制表示2^16，每一度为2^16/360。

//360°--2^16,phase_in = 16bits (input [15:0] phase_in)
//1°--2^16/360
`define rot0  'h2000    //45
`define rot1  'h12e4    //26.5651
`define rot2  'h09fb    //14.0362
`define rot3  'h0511    //7.1250
`define rot4  'h028b    //3.5763
`define rot5  'h0145    //1.7899
`define rot6  'h00a3    //0.8952
`define rot7  'h0051    //0.4476
`define rot8  'h0028    //0.2238
`define rot9  'h0014    //0.1119
`define rot10 'h000a    //0.0560
`define rot11 'h0005    //0.0280
`define rot12 'h0003    //0.0140
`define rot13 'h0002    //0.0070
`define rot14 'h0001    //0.0035
`define rot15 'h0000    //0.0018

然后是流水线级数定义、增益放大倍数以及中间结果位宽定义。流水线级数16，为了满足精度要求，有文献指出流水线级数必须大于等于角度位宽16（针对正弦余弦计算的CORDIC算法优化及其FPGA实现）。增益放大2^16，为了避免溢出状况中间结果（x，y，z）定义为17为，最高位作为符号位判断，1为负数，0为正数。

module cordic
(
    input clk,

    input [:] phase_in,
    output reg signed [:] eps,
    output reg signed [:] sin,
    output reg signed [:] cos
);
parameter PIPELINE = ;

parameter K = 'h9b74;
//gian k=0.607253*2^16,9b74,n means the number pipeline
//pipeline 16-level    //maybe overflow,matlab result not overflow
//MSB is signed bit,transform the sin and cos according to phase_in[15:14]
reg signed [:] x0=,y0=,z0=;
reg signed [:] x1=,y1=,z1=;
reg signed [:] x2=,y2=,z2=;
reg signed [:] x3=,y3=,z3=;
reg signed [:] x4=,y4=,z4=;
reg signed [:] x5=,y5=,z5=;
reg signed [:] x6=,y6=,z6=;
reg signed [:] x7=,y7=,z7=;
reg signed [:] x8=,y8=,z8=;
reg signed [:] x9=,y9=,z9=;
reg signed [:] x10=,y10=,z10=;
reg signed [:] x11=,y11=,z11=;
reg signed [:] x12=,y12=,z12=;
reg signed [:] x13=,y13=,z13=;
reg signed [:] x14=,y14=,z14=;
reg signed [:] x15=,y15=,z15=;
reg signed [:] x16=,y16=,z16=;

还需要定义memory型寄存器数组并初始化为0，用于寄存输入角度高2位的值。

reg [:] quadrant [PIPELINE:];
integer i;
initial
begin
    for(i=;i<=PIPELINE;i=i+)
    quadrant[i] = 'b0;
end

接着，是对输入角度象限处理，将角度都转换到第一象限，方便处理。输入角度值最高两位赋值0，即转移到第一象限[0°,90°]。此外，完成x0，y0和z0的初始化，并增加一位符号位。

always @ (posedge clk)//stage 0,not pipeline
begin
    x0 <= {'b0,K}; //add one signed bit,0 means positive
    y0 <= 'b0;
    z0 <= {'b0,phase_in[13:0]};//control the phase_in to the range[0-Pi/2]
end

接下来根据剩余待旋转角度z的符号位进行16次迭代处理，即完成16级流水线处理。

always @ (posedge clk)//stage 1
begin
  if(z0[])//the diff is negative so clockwise
  begin
      x1 <= x0 + y0;
      y1 <= x0 - y0;
      z1 <= z0 + `rot0;
  end
  else
  begin
      x1 <= x0 - y0;//x1 <= x0;
      y1 <= x0 + y0;//y1 <= x0;
      z1 <= z0 - `rot0;//reversal 45
  end
end

always @ (posedge clk)//stage 2
begin
    if(z1[])//the diff is negative so clockwise
    begin
        x2 <= x1 + (y1>>>'d1);
        y2 <= y1 - (x1>>>'d1);
        z2 <= z1 + `rot1;//clockwise 26
    end
    else
    begin
        x2 <= x1 - (y1>>>'d1);
        y2 <= y1 + (x1>>>'d1);
        z2 <= z1 - `rot1;//anti-clockwise 26
    end
end

always @ (posedge clk)//stage 3
begin
    if(z2[])//the diff is negative so clockwise
    begin
        x3 <= x2 + (y2>>>'d2); //right shift n bits,divide 2^n
        y3 <= y2 - (x2>>>'d2); //left adds n bits of MSB,in first quadrant x or y are positive,MSB =0 ？？
        z3 <= z2 + `rot2;//clockwise 14    //difference of positive and negtive number and no round(4,5)
    end
    else
    begin
        x3 <= x2 - (y2>>>'d2);
        y3 <= y2 + (x2>>>'d2);
        z3 <= z2 - `rot2;//anti-clockwise 14
    end
end

always @ (posedge clk)//stage 4
begin
    if(z3[])
    begin
        x4 <= x3 + (y3>>>'d3);
        y4 <= y3 - (x3>>>'d3);
        z4 <= z3 + `rot3;//clockwise 7
    end
    else
    begin
        x4 <= x3 - (y3>>>'d3);
        y4 <= y3 + (x3>>>'d3);
        z4 <= z3 - `rot3;//anti-clockwise 7
    end
end

always @ (posedge clk)//stage 5
begin
    if(z4[])
    begin
        x5 <= x4 + (y4>>>'d4);
        y5 <= y4 - (x4>>>'d4);
        z5 <= z4 + `rot4;//clockwise 3
    end
    else
    begin
        x5 <= x4 - (y4>>>'d4);
        y5 <= y4 + (x4>>>'d4);
        z5 <= z4 - `rot4;//anti-clockwise 3
    end
end

always @ (posedge clk)//STAGE 6
begin
    if(z5[])
    begin
        x6 <= x5 + (y5>>>'d5);
        y6 <= y5 - (x5>>>'d5);
        z6 <= z5 + `rot5;//clockwise 1
    end
    else
    begin
        x6 <= x5 - (y5>>>'d5);
        y6 <= y5 + (x5>>>'d5);
        z6 <= z5 - `rot5;//anti-clockwise 1
    end
end

always @ (posedge clk)//stage 7
begin
    if(z6[])
    begin
        x7 <= x6 + (y6>>>'d6);
        y7 <= y6 - (x6>>>'d6);
        z7 <= z6 + `rot6;
    end
    else
    begin
        x7 <= x6 - (y6>>>'d6);
        y7 <= y6 + (x6>>>'d6);
        z7 <= z6 - `rot6;
    end
end

always @ (posedge clk)//stage 8
begin
    if(z7[])
    begin
        x8 <= x7 + (y7>>>'d7);
        y8 <= y7 - (x7>>>'d7);
        z8 <= z7 + `rot7;
    end
    else
    begin
        x8 <= x7 - (y7>>>'d7);
        y8 <= y7 + (x7>>>'d7);
        z8 <= z7 - `rot7;
    end
end

always @ (posedge clk)//stage 9
begin
    if(z8[])
    begin
        x9 <= x8 + (y8>>>'d8);
        y9 <= y8 - (x8>>>'d8);
        z9 <= z8 + `rot8;
    end
    else
    begin
        x9 <= x8 - (y8>>>'d8);
        y9 <= y8 + (x8>>>'d8);
        z9 <= z8 - `rot8;
    end
end

always @ (posedge clk)//stage 10
begin
    if(z9[])
    begin
        x10 <= x9 + (y9>>>'d9);
        y10 <= y9 - (x9>>>'d9);
        z10 <= z9 + `rot9;
    end
    else
    begin
        x10 <= x9 - (y9>>>'d9);
        y10 <= y9 + (x9>>>'d9);
        z10 <= z9 - `rot9;
    end
end

always @ (posedge clk)//stage 11
begin
    if(z10[])
    begin
        x11 <= x10 + (y10>>>'d10);
        y11 <= y10 - (x10>>>'d10);
        z11 <= z10 + `rot10;
    end
    else
    begin
        x11 <= x10 - (y10>>>'d10);
        y11 <= y10 + (x10>>>'d10);
        z11 <= z10 - `rot10;
    end
end

always @ (posedge clk)//stage 12
begin
    if(z11[])
    begin
        x12 <= x11 + (y11>>>'d11);
        y12 <= y11 - (x11>>>'d11);
        z12 <= z11 + `rot11;
    end
    else
    begin
        x12 <= x11 - (y11>>>'d11);
        y12 <= y11 + (x11>>>'d11);
        z12 <= z11 - `rot11;
    end
end

always @ (posedge clk)//stage 13
begin
    if(z12[])
    begin
        x13 <= x12 + (y12>>>'d12);
        y13 <= y12 - (x12>>>'d12);
        z13 <= z12 + `rot12;
    end
    else
    begin
        x13 <= x12 - (y12>>>'d12);
        y13 <= y12 + (x12>>>'d12);
        z13 <= z12 - `rot12;
    end
end

always @ (posedge clk)//stage 14
begin
    if(z13[])
    begin
        x14 <= x13 + (y13>>>'d13);
        y14 <= y13 - (x13>>>'d13);
        z14 <= z13 + `rot13;
    end
    else
    begin
        x14 <= x13 - (y13>>>'d13);
        y14 <= y13 + (x13>>>'d13);
        z14 <= z13 - `rot13;
    end
end

always @ (posedge clk)//stage 15
begin
    if(z14[])
    begin
        x15 <= x14 + (y14>>>'d14);
        y15 <= y14 - (x14>>>'d14);
        z15 <= z14 + `rot14;
    end
    else
    begin
        x15 <= x14 - (y14>>>'d14);
        y15 <= y14 + (x14>>>'d14);
        z15 <= z14 - `rot14;
    end
end

always @ (posedge clk)//stage 16
begin
    if(z15[])
    begin
        x16 <= x15 + (y15>>>'d15);
        y16 <= y15 - (x15>>>'d15);
        z16 <= z15 + `rot15;
    end
    else
    begin
        x16 <= x15 - (y15>>>'d15);
        y16 <= y15 + (x15>>>'d15);
        z16 <= z15 - `rot15;
    end
end

其中使用到了算数右移（>>>）运算、所以在之前声明时将相应的reg/wire均声明为signed类型。这一点在【1】的最后也有说明。

需要注意的是这里的算数移位运算（这一运算的详细过程在【3】中进行了说明），与之区分的是逻辑移位运算。

二者规则为：

逻辑左移和右移，空出的位均补零。

算数左移与逻辑左移相同，都在低位补零；算数右移、移出的高位比特使用符号位填充（0正1负）

举例说明，对8'b_1011_0111进行逻辑、算数移位的结果如下图所示：

比如这里的原数值是8'b10110111、为负数（补码形式）、换算成十进制为-73.

算数右移一位之后的结果是8'b11011011、由补码换算成原码再换算为十进制为-37.

由于进行了象限的转换，最终流水结果需要根据象限进行转换为正确的值。这里寄存17次高2位角度输入值，配合流水线结果用于象限判断，并完成转换。

//according to the pipeline,register phase_in[15:14]
always @ (posedge clk)
begin
quadrant[] <= phase_in[:];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
quadrant[] <= quadrant[];
end

最后，根据寄存的高2位角度输入值，利用三角函数关系，得出最后的结果，其中负数进行了补码操作。

//alter register, according to quadrant[16] to transform the result to the right result
always @ (posedge clk)
    eps <= z16;

always @ (posedge clk) begin
case(quadrant[]) //or 15
'b00:begin //if the phase is in first quadrant,the sin(X)=sin(A),cos(X)=cos(A)
        cos <= x16;
        sin <= y16;
        end
'b01:begin //if the phase is in second quadrant,the sin(X)=sin(A+90)=cosA,cos(X)=cos(A+90)=-sinA
        cos <= ~(y16) + 'b1;//-sin
        sin <= x16;//cos
        end
'b10:begin //if the phase is in third quadrant,the sin(X)=sin(A+180)=-sinA,cos(X)=cos(A+180)=-cosA
        cos <= ~(x16) + 'b1;//-cos
        sin <= ~(y16) + 'b1;//-sin
        end
'b11:begin //if the phase is in forth quadrant,the sin(X)=sin(A+270)=-cosA,cos(X)=cos(A+270)=sinA
        cos <= y16;//sin
        sin <= ~(x16) + 'b1;//-cos
        end
endcase
end

完整代码：

//360°--2^16,phase_in = 16bits (input [15:0] phase_in)
//1°--2^16/360
`define rot0  'h2000    //45
`define rot1  'h12e4    //26.5651
`define rot2  'h09fb    //14.0362
`define rot3  'h0511    //7.1250
`define rot4  'h028b    //3.5763
`define rot5  'h0145    //1.7899
`define rot6  'h00a3    //0.8952
`define rot7  'h0051    //0.4476
`define rot8  'h0028    //0.2238
`define rot9  'h0014    //0.1119
`define rot10 'h000a    //0.0560
`define rot11 'h0005    //0.0280
`define rot12 'h0003    //0.0140
`define rot13 'h0002    //0.0070
`define rot14 'h0001    //0.0035
`define rot15 'h0000    //0.0018

module cordic
(
    input clk,
    //input rst_n,
    //input ena,
    input [:] phase_in,
    output reg signed [:] eps,
    output reg signed [:] sin,
    output reg signed [:] cos
);
parameter PIPELINE = ;
//parameter K = 16'h4dba;//k=0.607253*2^15
parameter K = 'h9b74;//gian k=0.607253*2^16,9b74,n means the number pipeline
//pipeline 16-level    //maybe overflow,matlab result not overflow
//MSB is signed bit,transform the sin and cos according to phase_in[15:14]
reg signed [:] x0=,y0=,z0=;
reg signed [:] x1=,y1=,z1=;
reg signed [:] x2=,y2=,z2=;
reg signed [:] x3=,y3=,z3=;
reg signed [:] x4=,y4=,z4=;
reg signed [:] x5=,y5=,z5=;
reg signed [:] x6=,y6=,z6=;
reg signed [:] x7=,y7=,z7=;
reg signed [:] x8=,y8=,z8=;
reg signed [:] x9=,y9=,z9=;
reg signed [:] x10=,y10=,z10=;
reg signed [:] x11=,y11=,z11=;
reg signed [:] x12=,y12=,z12=;
reg signed [:] x13=,y13=,z13=;
reg signed [:] x14=,y14=,z14=;
reg signed [:] x15=,y15=,z15=;
reg signed [:] x16=,y16=,z16=;

reg [:] quadrant [PIPELINE:];
integer i;
initial
begin
    for(i=;i<=PIPELINE;i=i+)
    quadrant[i] = 'b0;
end

always @ (posedge clk)//stage 0,not pipeline
begin
    x0 <= {'b0,K}; //add one signed bit,0 means positive
    y0 <= 'b0;
    z0 <= {'b0,phase_in[13:0]};//control the phase_in to the range[0-Pi/2]
end

always @ (posedge clk)//stage 1
begin
  if(z0[])//the diff is negative so clockwise
  begin
      x1 <= x0 + y0;
      y1 <= x0 - y0;
      z1 <= z0 + `rot0;
  end
  else
  begin
      x1 <= x0 - y0;//x1 <= x0;
      y1 <= x0 + y0;//y1 <= x0;
      z1 <= z0 - `rot0;//reversal 45
  end
end

always @ (posedge clk)//stage 2
begin
    if(z1[])//the diff is negative so clockwise
    begin
        x2 <= x1 + (y1>>>'d1);
        y2 <= y1 - (x1>>>'d1);
        z2 <= z1 + `rot1;//clockwise 26
    end
    else
    begin
        x2 <= x1 - (y1>>>'d1);
        y2 <= y1 + (x1>>>'d1);
        z2 <= z1 - `rot1;//anti-clockwise 26
    end
end

always @ (posedge clk)//stage 3
begin
    if(z2[])//the diff is negative so clockwise
    begin
        x3 <= x2 + (y2>>>'d2); //right shift n bits,divide 2^n
        y3 <= y2 - (x2>>>'d2); //left adds n bits of MSB,in first quadrant x or y are positive,MSB =0 ？？
        z3 <= z2 + `rot2;//clockwise 14    //difference of positive and negtive number and no round(4,5)
    end
    else
    begin
        x3 <= x2 - (y2>>>'d2);
        y3 <= y2 + (x2>>>'d2);
        z3 <= z2 - `rot2;//anti-clockwise 14
    end
end

always @ (posedge clk)//stage 4
begin
    if(z3[])
    begin
        x4 <= x3 + (y3>>>'d3);
        y4 <= y3 - (x3>>>'d3);
        z4 <= z3 + `rot3;//clockwise 7
    end
    else
    begin
        x4 <= x3 - (y3>>>'d3);
        y4 <= y3 + (x3>>>'d3);
        z4 <= z3 - `rot3;//anti-clockwise 7
    end
end

always @ (posedge clk)//stage 5
begin
    if(z4[])
    begin
        x5 <= x4 + (y4>>>'d4);
        y5 <= y4 - (x4>>>'d4);
        z5 <= z4 + `rot4;//clockwise 3
    end
    else
    begin
        x5 <= x4 - (y4>>>'d4);
        y5 <= y4 + (x4>>>'d4);
        z5 <= z4 - `rot4;//anti-clockwise 3
    end
end

always @ (posedge clk)//STAGE 6
begin
    if(z5[])
    begin
        x6 <= x5 + (y5>>>'d5);
        y6 <= y5 - (x5>>>'d5);
        z6 <= z5 + `rot5;//clockwise 1
    end
    else
    begin
        x6 <= x5 - (y5>>>'d5);
        y6 <= y5 + (x5>>>'d5);
        z6 <= z5 - `rot5;//anti-clockwise 1
    end
end

always @ (posedge clk)//stage 7
begin
    if(z6[])
    begin
        x7 <= x6 + (y6>>>'d6);
        y7 <= y6 - (x6>>>'d6);
        z7 <= z6 + `rot6;
    end
    else
    begin
        x7 <= x6 - (y6>>>'d6);
        y7 <= y6 + (x6>>>'d6);
        z7 <= z6 - `rot6;
    end
end

always @ (posedge clk)//stage 8
begin
    if(z7[])
    begin
        x8 <= x7 + (y7>>>'d7);
        y8 <= y7 - (x7>>>'d7);
        z8 <= z7 + `rot7;
    end
    else
    begin
        x8 <= x7 - (y7>>>'d7);
        y8 <= y7 + (x7>>>'d7);
        z8 <= z7 - `rot7;
    end
end

always @ (posedge clk)//stage 9
begin
    if(z8[])
    begin
        x9 <= x8 + (y8>>>'d8);
        y9 <= y8 - (x8>>>'d8);
        z9 <= z8 + `rot8;
    end
    else
    begin
        x9 <= x8 - (y8>>>'d8);
        y9 <= y8 + (x8>>>'d8);
        z9 <= z8 - `rot8;
    end
end

always @ (posedge clk)//stage 10
begin
    if(z9[])
    begin
        x10 <= x9 + (y9>>>'d9);
        y10 <= y9 - (x9>>>'d9);
        z10 <= z9 + `rot9;
    end
    else
    begin
        x10 <= x9 - (y9>>>'d9);
        y10 <= y9 + (x9>>>'d9);
        z10 <= z9 - `rot9;
    end
end

always @ (posedge clk)//stage 11
begin
    if(z10[])
    begin
        x11 <= x10 + (y10>>>'d10);
        y11 <= y10 - (x10>>>'d10);
        z11 <= z10 + `rot10;
    end
    else
    begin
        x11 <= x10 - (y10>>>'d10);
        y11 <= y10 + (x10>>>'d10);
        z11 <= z10 - `rot10;
    end
end

always @ (posedge clk)//stage 12
begin
    if(z11[])
    begin
        x12 <= x11 + (y11>>>'d11);
        y12 <= y11 - (x11>>>'d11);
        z12 <= z11 + `rot11;
    end
    else
    begin
        x12 <= x11 - (y11>>>'d11);
        y12 <= y11 + (x11>>>'d11);
        z12 <= z11 - `rot11;
    end
end

always @ (posedge clk)//stage 13
begin
    if(z12[])
    begin
        x13 <= x12 + (y12>>>'d12);
        y13 <= y12 - (x12>>>'d12);
        z13 <= z12 + `rot12;
    end
    else
    begin
        x13 <= x12 - (y12>>>'d12);
        y13 <= y12 + (x12>>>'d12);
        z13 <= z12 - `rot12;
    end
end

always @ (posedge clk)//stage 14
begin
    if(z13[])
    begin
        x14 <= x13 + (y13>>>'d13);
        y14 <= y13 - (x13>>>'d13);
        z14 <= z13 + `rot13;
    end
    else
    begin
        x14 <= x13 - (y13>>>'d13);
        y14 <= y13 + (x13>>>'d13);
        z14 <= z13 - `rot13;
    end
end

always @ (posedge clk)//stage 15
begin
    if(z14[])
    begin
        x15 <= x14 + (y14>>>'d14);
        y15 <= y14 - (x14>>>'d14);
        z15 <= z14 + `rot14;
    end
    else
    begin
        x15 <= x14 - (y14>>>'d14);
        y15 <= y14 + (x14>>>'d14);
        z15 <= z14 - `rot14;
    end
end

always @ (posedge clk)//stage 16
begin
    if(z15[])
    begin
        x16 <= x15 + (y15>>>'d15);
        y16 <= y15 - (x15>>>'d15);
        z16 <= z15 + `rot15;
    end
    else
    begin
        x16 <= x15 - (y15>>>'d15);
        y16 <= y15 + (x15>>>'d15);
        z16 <= z15 - `rot15;
    end
end

//according to the pipeline,register phase_in[15:14]
always @ (posedge clk)
begin
  quadrant[] <= phase_in[:];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
  quadrant[] <= quadrant[];
end

//alter register, according to quadrant[16] to transform the result to the right result
always @ (posedge clk)
    eps <= z16;

always @ (posedge clk) begin
case(quadrant[]) //or 15
'b00:begin //if the phase is in first quadrant,the sin(X)=sin(A),cos(X)=cos(A)
        cos <= x16;
        sin <= y16;
        end
'b01:begin //if the phase is in second quadrant,the sin(X)=sin(A+90)=cosA,cos(X)=cos(A+90)=-sinA
        cos <= ~(y16) + 'b1;//-sin
        sin <= x16;//cos
        end
'b10:begin //if the phase is in third quadrant,the sin(X)=sin(A+180)=-sinA,cos(X)=cos(A+180)=-cosA
        cos <= ~(x16) + 'b1;//-cos
        sin <= ~(y16) + 'b1;//-sin
        end
'b11:begin //if the phase is in forth quadrant,the sin(X)=sin(A+270)=-cosA,cos(X)=cos(A+270)=sinA
        cos <= y16;//sin
        sin <= ~(x16) + 'b1;//-cos
        end
endcase
end

endmodule

Whole Code

testbench测试代码：

`timescale  ps/  ps
module cordic_tb;
// test vector input registers
reg arst;
reg clk;

reg [:] phase = 'h2000;
// wires
wire signed [:] cosine_out;
wire signed [:] eps_out;
wire signed [:] sine_out;
//
localparam coef=;
// assign statements (if any)
cordic i1 (
// port map - connection between master ports and signals/registers   

    .clk(clk),
    .cos(cosine_out),
    .eps(eps_out),
    .phase_in(phase),
    .sin(sine_out)
);
initial
begin
  clk=;
  #(*coef) $stop;
end
always #(*coef) clk=~clk;
//
always @(negedge clk)
begin
    phase=phase+'h0100;
end
endmodule

Testbench

3、Modelsim仿真结果

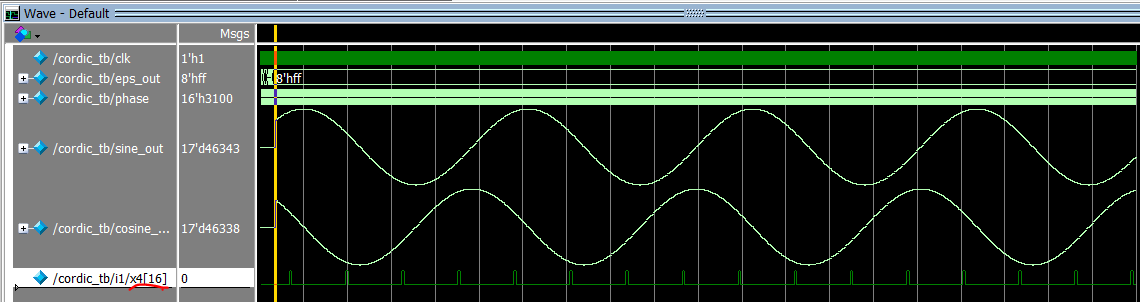
仿真结果的补充说明：

（1）程序全程未使用复位信号，testbench中第一个计算的角度为16'h2000也就是45度，如果以图示时刻为0时刻、仿真结果对应的波形即分别为sin(x+π/4)和cos(x+π/4)的波形。作为参考，0.5*√2*65535≈46340.

（2）关于运算过程中的位数溢出

根据仿真结果，本测试例下，x4出现过16位位数溢出。

（3）关于流水线设计的理解

前文提到过实现CORDIC迭代算法时可以使用反馈结构（只使用一级）、也可以使用流水线结构（多级），如果任务是只单独计算一个角度的正弦或者余弦值，那么所需要的迭代次数或者说消耗的时钟周期数量其实是相同的，本设计中为16个时钟。

流水线结构的威力是在连续、源源不断地计算一组多个角度的正余弦值的时候才展现出来，当初始流水线被填满之后，每经过一个时钟周期、都会在输出上获得一个更新的角度的正余弦结果值，上图仿真结果图中黄色cursor左侧的时间段内、流水线即被逐步填满。

换句话说，如果现在的任务是要计算n个角度的正余弦值、计算一个角度需要的迭代次数为x，反馈结构需要的时长为（n*x）个时钟周期，流水线结构只需要（n+x-1）个时钟周期。