堆排序 Heapsort

Prime + Heap 简直神了 时间优化好多，顺便就把Heapsort给撸了一发

具体看图

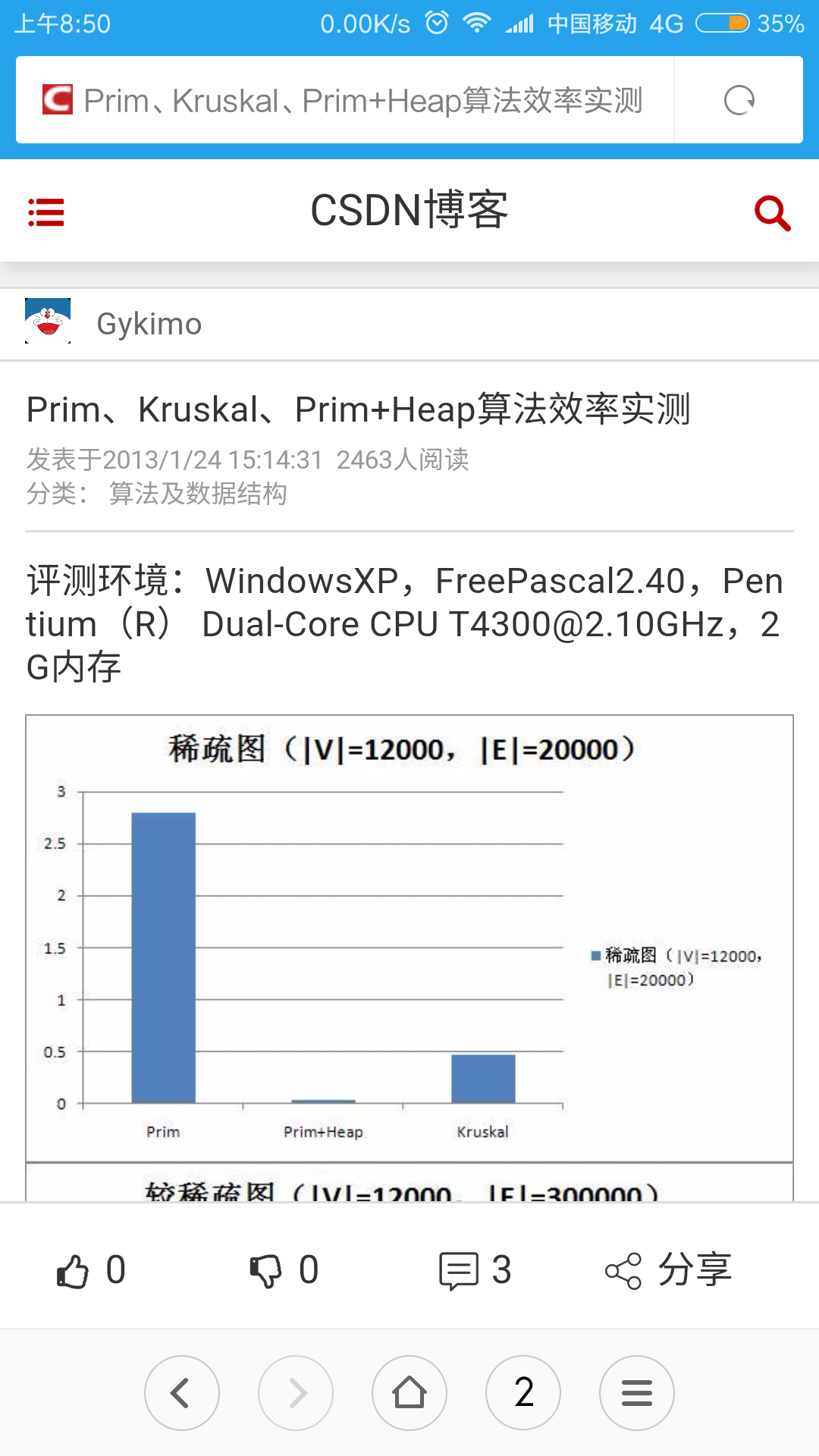
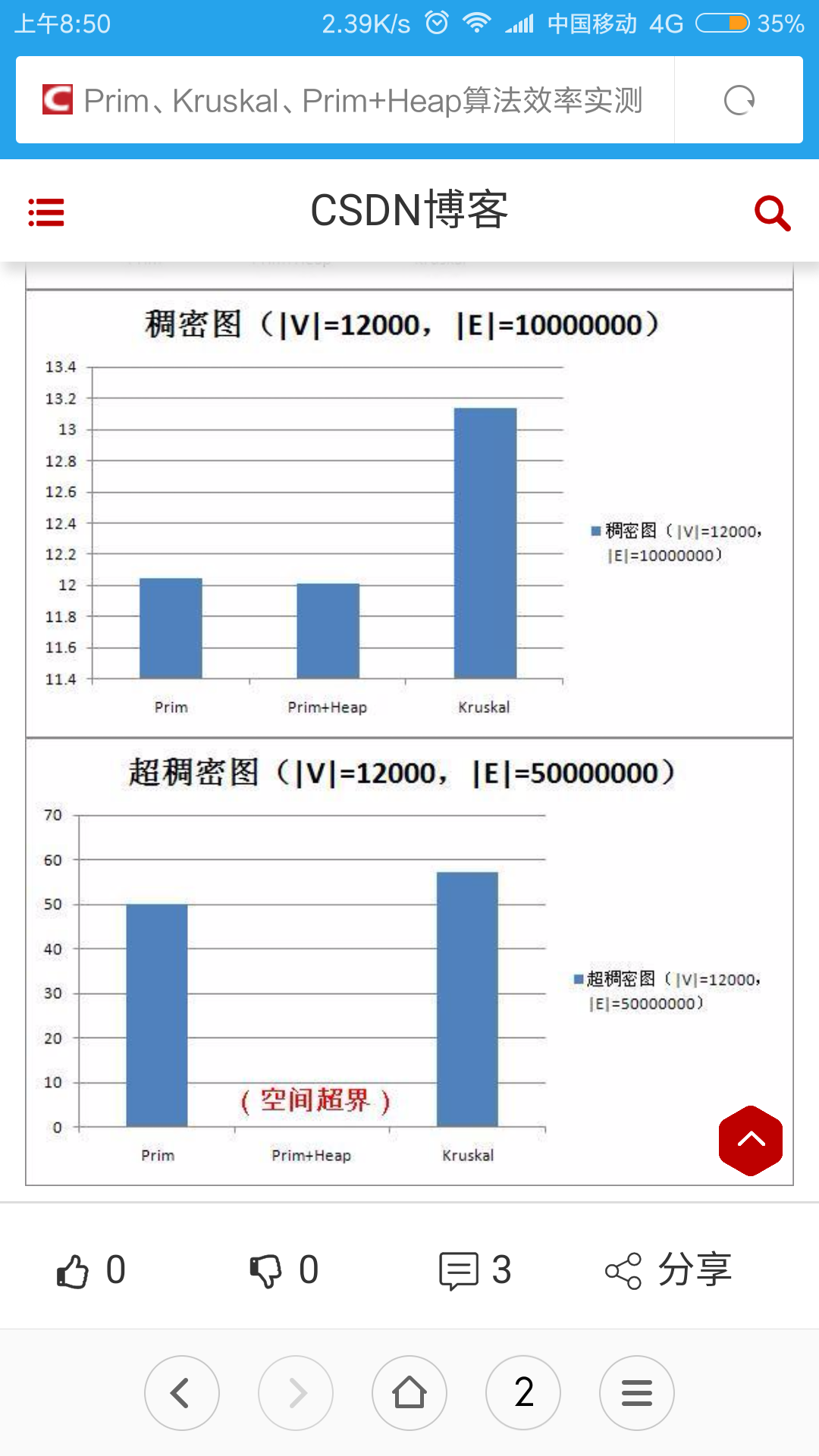
Heapsort利用完全二叉树+大（小）顶锥的结构每次将锥定元素和锥最末尾的元素交换 同时大（小）顶锥元素数 -1，迭代n-1次级OK了

我这里的是按从小到大拍的

 //堆排序 时间复杂度为 O(nlogn)

 void Swap(int *a, int i, int j)   //交换a[i] 和 a[j] 的值
 {
     int temp = a[i];
     a[i] = a[j];
     a[j] = temp;
 }

 void Heapadjust(int *a,int s,int n)     //调整父亲节点，使其满足大（小）顶锥结构 s为父亲节点下标
 {
     int temp = a[s];

     for(int i=*s; i<n; i*=)
     {
         if(i<n && a[i] < a[i+])
             i++;
         if(temp >= a[i])
             break;
         a[s] = a[i];
         s = i;
     }
     a[s] = temp;
 }

 void Heapsort(int *a, int n)  //对*a 数组排序，从a[1] - a[n] 排序
 {
     for(int i=n/; i>; i--)
         Heapadjust(a,i,n);

     for(int i=n; i>; i--)
     {
         Swap(a,,i);
         Heapadjust(a,,i-);
     }
 }