Algorithm --> DFS和BFS

定义结点

struct MGraph
{
    int vexs[MAXVEX];        //顶点数组
    int arc[MAXVEX][MAXVEX]; //邻接矩阵
    int numVertex, numEdges;  //定点数 边数
};

深度优先遍历

图示

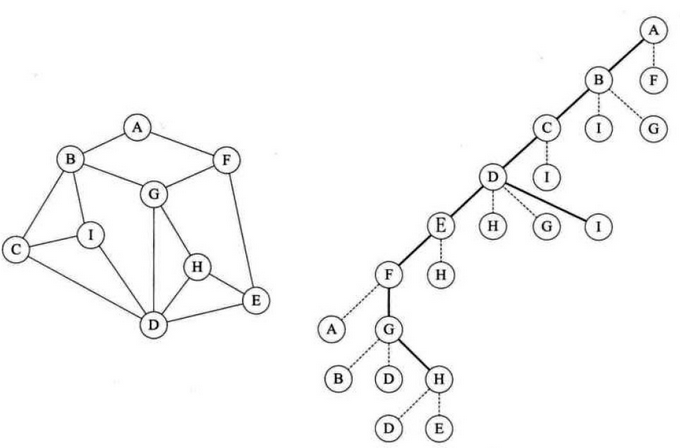
参考代码

bool visited[MAX];
void DFS(MGraph G, int i)
{
    cout << G.vexs[i] << " ";
　　 visited[i] = true;
    for (int j = ; j < G.numVertex; ++j)
    {
        if (G.arc[i][j] ==  && !visited[j])
            DFS(G, j);
       }
}
void DFSTranverse(MGraph G)
{
    for (int i = ; i < G.numVertex; ++i)
        visited[i] = false;
    for (int i =  ; i < G.numVertex; ++i)  //如果是连通图，只执行一次
    {
        if (!visited[i])
            DFS(G, i);
    }
}

广度优先遍历

图示

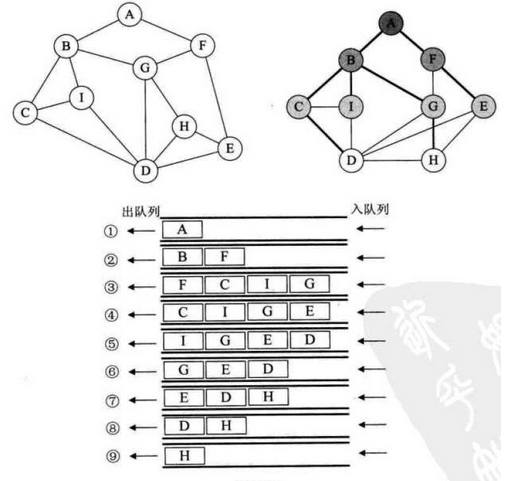
参考代码

void BFSTranverse(MGraph G)
{
    queue<int> q;
    bool visited[G.numVertex];
    for (int i = ; i < G.numVertex; ++i)
        visited[i] = false;
    for (int i = ; i < G.numVertex; ++i)
    {
        if (!visited[i])
        {
            cout << G.vexs[i] << " ";
            q.push(i);
             visited[i] = true;
             while (!q.empty())
              {
                   int k = q.top();
                   q.pop();
                    for (int j = ; j < G.numVertex; ++j)
                    {
                        if (G.arc[i][j] ==  && !visitied(j))
                            {
                                cout << G.vexs[j] << " ";
                                visited[j] = true;
                                q.push(j);
                            }
                     }
                }
            }
　　　}//for
}

另一种：

void BFS()
{
    visited[] = ;
    queue q;
    q.push();
    while(!q.empty())
    {
       int top = q.front();
       cout << top<<" ";//输出
       q.pop();
       int i ;
       for(i = ; i <= M; ++i)
       {
        if(visited[i] ==  && matrix[top - ][i -  ] == )
        {
         visited[i] = ;
         q.push(i);
        }
       }
    }
}

/******************* 2015.07.06 update ************************/

BFS:

#include <stdio.h>

int o[][] = { { ,  }, { ,  }, { -,  }, { , - } };
int map[][] = {  };

int queue[][] = {};
int front = ;
int back = ;
int parent[][][] = {};

void BFS(int sY, int sX, int eY, int eX)
{
    queue[back][] = sY;
    queue[back++][] = sX;
    map[sY][sX] = ;
    while (front < back)
    {
        int Y = queue[front][];
        int X = queue[front][];
        for (int i = ; i < ; i++)
        {
            int newY = Y + o[i][];
            int newX = X + o[i][];
            if (map[newY][newX] == )continue;
            if (map[newY][newX] > (map[Y][X] + ))
            {
                map[newY][newX] = map[Y][X] + ;
                parent[newY][newX][] = Y;
                parent[newY][newX][] = X;
                if ((newY == eY) && (newX == eX))
                {
                    return;
                }
                queue[back][] = newY;
                queue[back++][] = newX;
            }
        }

        front++;
    }
}

int main(int argc, char** argv)
{
    freopen("input.txt", "r", stdin);
    int N;
    scanf("%d\n", &N);
    for (int case_num = ; case_num < N; case_num++)
    {
        for (int i = ; i <= ; i++)
        {
            for (int j = ; j <= ; j++)
            {
                scanf("%d\n", &map[i][j]);
                if (map[i][j] == )map[i][j] = ;
            }
            scanf("\n");
        }
    }

    BFS(, , , );
    if (map[][] == )printf("failed\n");
    else printf("%d\n", map[][]);

    int x = , y = ;
    int stack[][] = {};
    int step = ;
    while (x >  || y > )
    {
        stack[step][] = y;
        stack[step++][] = x;
        int newY = parent[y][x][];
        int newX = parent[y][x][];
        x = newX;
        y = newY;
    }

    for (int i = step - ; i >= ; i--)
    {
        printf("%d %d\n", stack[i][], stack[i][]);
    }
}

DFS:

#include <stdio.h>

int o[][] = { { ,  }, { ,  }, { -,  }, { , - } };
int map[][] = {};
int minStep = ;
int stack[][] = {};
int step = ;
int minStack[][] = {};

void DFS(int sY, int sX, int eY, int eX)
{
    if (step >= minStep)return;
    if (map[sY][sX] == )return;
    stack[step][] = sY;
    stack[step++][] = sX;
    map[sY][sX] = ;
    if ((sY == eY) && (sX == eX))
    {
        if (minStep > step)
        {
            minStep = step;
            for (int i = ; i < step; i++)
            {
                minStack[i][] = stack[i][];
                minStack[i][] = stack[i][];
            }
        }
        map[sY][sX] = ;
        step--;
        return;
    }
    for (int i = ; i < ; i++)
    {
        (DFS(sY + o[i][], sX + o[i][], eY, eX));
    }

    map[sY][sX] = ;
    step--;
    return;
}

int main(int argc, char** argv)
{
    freopen("input.txt", "r", stdin);
    int N;
    scanf("%d\n", &N);
    for (int case_num = ; case_num < N; case_num++)
    {
        for (int i = ; i <= ; i++)
        {
            for (int j = ; j <= ; j++)
            {
                scanf("%d\n", &map[i][j]);
            }
            scanf("\n");
        }
    }

    DFS(,,,);
    printf("%d\n", minStep-);
    for (int i = ; i < minStep; i++)
    {
        printf("%d %d\n", minStack[i][], minStack[i][]);
    }
    //if (ret)printf("success\n");
    //else printf("failed\n");
}

input: