WPF绘制光滑连续贝塞尔曲线

1.需求

WPF本身没有直接把点集合绘制成曲线的函数。可以通过贝塞尔曲线函数来绘制。　　

贝塞尔曲线类是：BezierSegment，三次贝塞尔曲线，通过两个控制点来控制开始和结束方向。

QuadraticBezierSegment，二次贝塞尔，通过一个控制点来控制弯曲方向。

本文使用的是三次。

图片来源维基百科

2.思路

参考文档是：https://www.cnblogs.com/pangliang/archive/2011/03/24/1993308.html

大值思路是根据当前点，前一个点，后一个点，再后一个点。共四个点，来生成一条三次贝塞尔曲线。

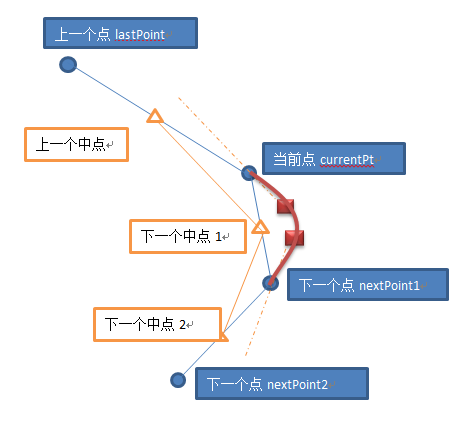
曲线需要（开始点，结束点，控制点1，控制点2），图中标识的两个红色点即是控制点。

代码主要是计算两个红色的控制点。

先计算相邻点的中点【橙色】。

再将中点的连线平移到相邻的位置【蓝色点】，取得虚线，得到虚线的端点【红色】。

红色，即为控制点。

3.主要代码

  /// <summary>
        /// 获得贝塞尔曲线
        /// </summary>
        /// <param name="currentPt">当前点</param>
        /// <param name="lastPt">上一个点</param>
        /// <param name="nextPt1">下一个点1</param>
        /// <param name="nextPt2">下一个点2</param>
        /// <returns></returns>
        private BezierSegment GetBezierSegment(Point currentPt, Point lastPt, Point nextPt1, Point nextPt2)
        {
            //计算中点
            var lastC = GetCenterPoint(lastPt, currentPt);
            var nextC1 = GetCenterPoint(currentPt, nextPt1); //贝塞尔控制点
            var nextC2 = GetCenterPoint(nextPt1, nextPt2);

            //计算相邻中点连线跟目的点的垂足
            //效果并不算太好，因为可能点在两个线上或者线的延长线上，计算会有误差
            //所以就直接使用中点平移方法。
            //var C1 = GetFootPoint(lastC, nextC1, currentPt);
            //var C2 = GetFootPoint(nextC1, nextC2, nextPt1);

            //计算“相邻中点”的中点
            var c1 = GetCenterPoint(lastC, nextC1);
            var c2 = GetCenterPoint(nextC1, nextC2);

            //计算【"中点"的中点】需要的点位移
            var controlPtOffset1 = currentPt - c1;
            var controlPtOffset2 = nextPt1 - c2;

            //移动控制点
            var controlPt1 = nextC1 + controlPtOffset1;
            var controlPt2 = nextC1 + controlPtOffset2;

            //如果觉得曲线幅度太大，可以将控制点向当前点靠近一定的系数。
            controlPt1 = controlPt1 + 0 * (currentPt - controlPt1);
            controlPt2 = controlPt2 + 0 * (nextPt1 - controlPt2);

            var bzs = new BezierSegment(controlPt1, controlPt2, nextPt1, true);
            return bzs;
        }

　　

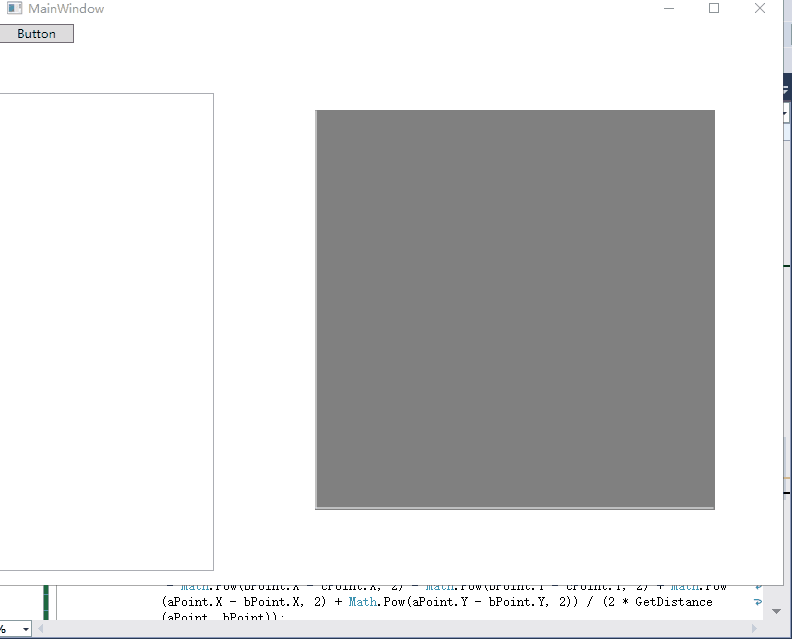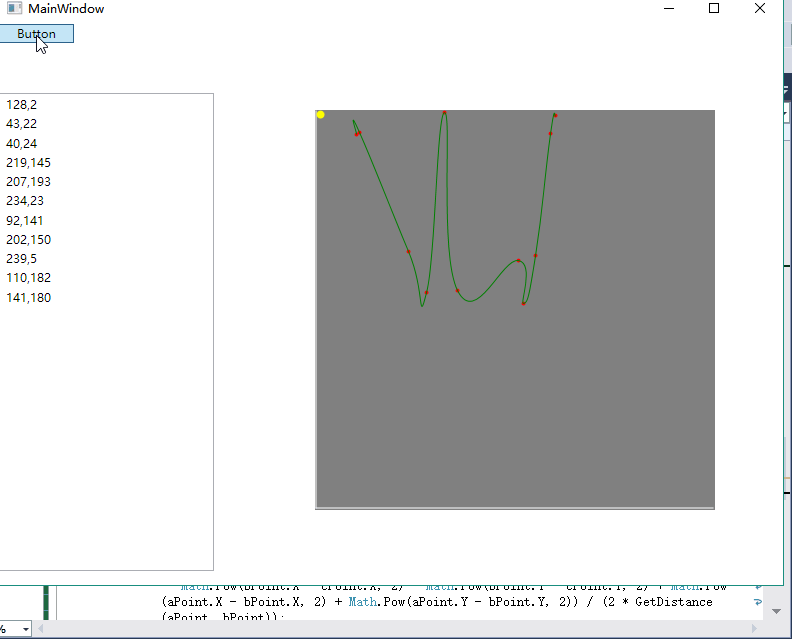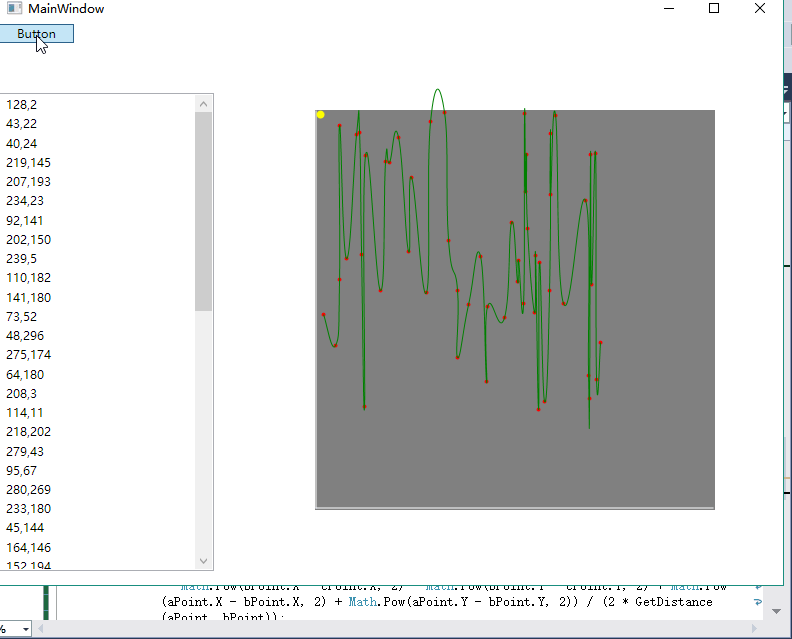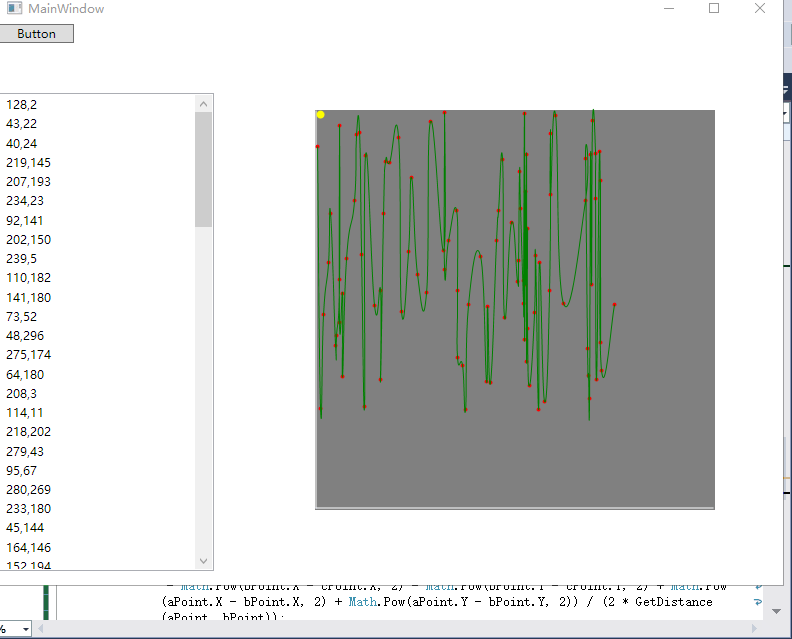
效果图如下：

4.源码下载

https://files.cnblogs.com/files/chlm/WPF%E5%85%89%E6%BB%91%E6%9B%B2%E7%BA%BF%E5%9B%BE.rar

感谢阅读，希望可以帮到你