HMM:隐马尔可夫模型HMM
http://blog.csdn.net/pipisorry/article/details/50722178
隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程,是在被建模的系统被认为是一个马尔可夫过程与未观测到的(隐藏的)的状态的统计马尔可夫模型。
在正常的马尔可夫模型中,状态对于观察者来说是直接可见的。这样状态的转换概率便是全部的参数。[马尔科夫模型HMM概述]
而在隐马尔可夫模型中,状态并不是直接可见的,但受状态影响的某些变量则是可见的。每一个状态在可能输出的符号上都有一概率分布。因此输出符号的序列能够透露出状态序列的一些信息。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。
HMM(隐马尔科夫模型)是自然语言处理中的一个基本模型,用途比较广泛,如汉语分词、词性标注及语音识别等,在NLP中占有很重要的地位。
与马尔科夫相比,隐马尔科夫模型则是双重随机过程,不仅状态转移之间是个随机事件,状态和输出之间也是一个随机过程,如下图所示:

此图中符号与之前描述马尔科夫时可能不同。
该图分为上下两行,上面那行就是一个马尔科夫转移过程,下面这一行则是输出,即我们可以观察到的值,现在,我们将上面那行的马尔科夫转移过程中的状态称为隐藏状态,下面的观察到的值称为观察状态,观察状态的集合表示为 O={O1,O2,O3,…OM}。
相应的,隐马尔科夫也比马尔科夫多了一个假设,即输出仅与当前状态有关,可以用如下公式表示:
P(O1,O2,…,Ot|S1,S2,…,St)=P(O1|S1)*P(O2|S2)*...*P(Ot|St)
其中,O1,O2,…,Ot为从时刻1到时刻t的观测状态序列,S1,S2,…,St则为隐藏状态序列。
另外,该假设又称为输出独立性假设。
隐马尔科夫模型(Hidden Markov Models)
回顾一下马尔科夫过程[马尔科夫模型]天气那个例子,一个隐士也许不能够直接获取到天气的观察情况,但是他有一些水藻。民间传说告诉我们水藻的状态与天气状态有一定的概率关系——天气和水藻的状态是紧密相关的。在这个例子中我们有两组状态,观察的状态(水藻的状态)和隐藏的状态(天气的状态)。我们希望为隐士设计一种算法,在不能够直接观察天气的情况下,通过水藻和马尔科夫假设来预测天气。
例子中,需要着重指出的是,隐藏状态的数目与观察状态的数目可以是不同的。一个包含三个状态的天气系统(晴天、多云、雨天)中,可以观察到4个等级的海藻湿润情况(干、稍干、潮湿、湿润)。在这种情况下,观察到的状态序列与隐藏过程有一定的概率关系。我们使用隐马尔科夫模型对这样的过程建模,这个模型包含了一个底层隐藏的随时间改变的马尔科夫过程,以及一个与隐藏状态某种程度相关的可观察到的状态集合。
下图显示的是天气例子中的隐藏状态和观察状态。
假设隐藏状态(实际的天气)由一个简单的一阶马尔科夫过程描述,那么它们之间都相互连接。
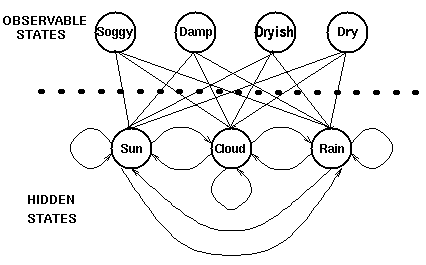
隐藏状态和观察状态之间的连接表示:在给定的马尔科夫过程中,一个特定的隐藏状态生成特定的观察状态的概率。这很清晰的表示了‘进入’一个观察状态的所有概率之和为1,在上面这个例子中就是Pr(Obs|Sun),Pr(Obs|Cloud) 及 Pr(Obs|Rain)之和。
Note:这里是把obs作为参数来用,就是说Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Sun) = 1;
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Cloud) = 1;
Sum_{Obs=Dry,Dryish,Damp,Soggy}(Obs|Rain) = 1;
除了定义了马尔科夫过程的概率关系,我们还有另一个矩阵,定义为混淆矩阵(confusion matrix),它包含了给定一个隐藏状态后得到的观察状态的概率。对于天气例子,混淆矩阵是:
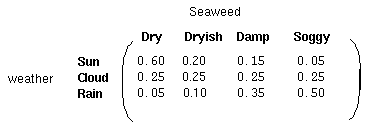
注意矩阵的每一行之和是1。
隐马尔科夫过程的定义
* 隐藏状态:一个系统的(真实)状态,可以由一个马尔科夫过程进行描述(例如,天气)。
* 观察状态:在这个过程中‘可视’的状态(例如,海藻的湿度)。
* pi向量:包含了(隐)模型在时间t=1时一个特殊的隐藏状态的概率(初始概率)。
* 状态转移矩阵:包含了一个隐藏状态到另一个隐藏状态的概率
* 混淆矩阵:包含了给定隐马尔科夫模型的某一个特殊的隐藏状态,观察到的某个观察状态的概率。
一个隐马尔科夫模型是一个三元组(pi, A, B)
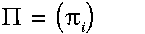 :初始化概率向量;
:初始化概率向量;
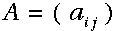 :状态转移矩阵;
:状态转移矩阵;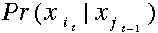
 :混淆矩阵;
:混淆矩阵;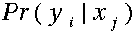
在状态转移矩阵及混淆矩阵中的每一个概率都是时间无关的——也就是说,当系统演化时这些矩阵并不随时间改变。实际上,这是马尔科夫模型关于真实世界最不现实的一个假设。
隐马模型基本要素及基本三问题
举个例子
举个常见的例子来引出下文,同时方便大家理解!比如我在不同天气状态下去做一些事情的概率不同,天气状态集合为{下雨,阴天,晴天},事情集合为{宅着,自习,游玩}。假如我们已经有了转移概率和输出概率,即P(天气A|天气B)和P(事情a|天气A)的概率都已知道,那么则有几个问题要问(注意,假设一天我那几件事情中的一件),
1.假如一周内的天气变化是 下雨->晴天->阴天->下雨->阴天->晴天->阴天,那么我这一周 自习->宅着->游玩->自习->游玩->宅着->自习的概率是多大?
2.假如我这一周做事序列是 自习->宅着->游玩->自习->游玩->宅着->自习,不知道天气状态的情况下这个做事序列的概率是多大?
3.假如一周内的天气变化是 下雨->晴天->阴天->下雨->阴天->晴天->阴天,那我们这一周最有可能的做事序列是什么?
4.假如我这一周做事序列是 自习->宅着->游玩->自习->游玩->宅着->自习,那么这一周的天气变化序列最有可能是什么?
HMM的三个基本要素
综上所述,我们可以得到隐马尔科夫的基本要素,即一个五元组{S,N,A,B,PI};
S:隐藏状态集合;
N:观察状态集合;
A:隐藏状态间的转移概率矩阵;
B:输出矩阵(即隐藏状态到输出状态的概率);
PI:初始概率分布(隐藏状态的初始概率分布);
其中,A,B,PI称为隐马尔科夫的参数,用X表示。
由上述问题可以引出隐马尔科夫的三个基本问题的其中两个。
HMM的三个基本问题
1. 给定模型(五元组),求某个观察序列O的概率(样例问题2)。
2. 给定模型和观察序列O,求可能性最大的隐藏状态序列(样例问题4)。
3. 对于给定的观察序列O,调整HMM的参数,使观察序列出现的概率最大。
一旦一个系统可以作为HMM被描述,就可以用来解决三个基本问题。
其中前两个是模式识别的问题:给定HMM求一个观察序列的概率(评估);搜索最有可能生成一个观察序列的隐藏状态序列(解码)。第三个问题是给定观察序列生成一个HMM(学习)。
a) 评估(Evaluation)
考虑这样的问题,我们有一些描述不同系统的隐马尔科夫模型(也就是一些( pi,A,B)三元组的集合)及一个观察序列。我们想知道哪一个HMM最有可能产生了这个给定的观察序列。例如,对于海藻来说,我们也许会有一个“夏季”模型和一个“冬季”模型,因为不同季节之间的情况是不同的——我们也许想根据海藻湿度的观察序列来确定当前的季节。
我们使用前向算法(forward algorithm)来计算给定隐马尔科夫模型(HMM)后的一个观察序列的概率,并因此选择最合适的隐马尔科夫模型(HMM)。
在语音识别中这种类型的问题发生在当一大堆数目的马尔科夫模型被使用,并且每一个模型都对一个特殊的单词进行建模时。一个观察序列从一个发音单词中形成,并且通过寻找对于此观察序列最有可能的隐马尔科夫模型(HMM)识别这个单词。
b) 解码( Decoding)
给定观察序列搜索最可能的隐藏状态序列。
另一个相关问题,也是最感兴趣的一个,就是搜索生成输出序列的隐藏状态序列。在许多情况下我们对于模型中的隐藏状态更感兴趣,因为它们代表了一些更有价值的东西,而这些东西通常不能直接观察到。
考虑海藻和天气这个例子,一个盲人隐士只能感觉到海藻的状态,但是他更想知道天气的情况,天气状态在这里就是隐藏状态。
我们使用Viterbi 算法(Viterbi algorithm)确定(搜索)已知观察序列及HMM下最可能的隐藏状态序列。
Viterbi算法(Viterbi algorithm)的另一广泛应用是自然语言处理中的词性标注。在词性标注中,句子中的单词是观察状态,词性(语法类别)是隐藏状态(注意对于许多单词,如wind,fish拥有不止一个词性)。对于每句话中的单词,通过搜索其最可能的隐藏状态,我们就可以在给定的上下文中找到每个单词最可能的词性标注。
C)学习(Learning)
根据观察序列生成隐马尔科夫模型。
第三个问题,也是与HMM相关的问题中最难的,根据一个观察序列(来自于已知的集合),以及与其有关的一个隐藏状态集,估计一个最合适的隐马尔科夫模型(HMM),也就是确定对已知序列描述的最合适的(pi,A,B)三元组。
当矩阵A和B不能够直接被(估计)测量时,前向-后向算法(forward-backward algorithm)被用来进行学习(参数估计),这也是实际应用中常见的情况。
wiki上一个关于HMM三个基本问题解释的例子
Alice 和Bob是好朋友,但是他们离得比较远,每天都是通过电话了解对方那天作了什么.Bob仅仅对三种活动感兴趣:公园散步,购物以及清理房间.他选择做什么事情只凭当天天气.Alice对于Bob所住的地方的天气情况并不了解,但是知道总的趋势.在Bob告诉Alice每天所做的事情基础上,Alice想要猜测Bob所在地的天气情况.
Alice认为天气的运行就像一个马尔可夫链. 其有两个状态 “雨”和”晴”,但是无法直接观察它们,也就是说,它们对于Alice是隐藏的.每天,Bob有一定的概率进行下列活动:”散步”, “购物”, 或 “清理”. 因为Bob会告诉Alice他的活动,所以这些活动就是Alice的观察数据.这整个系统就是一个隐马尔可夫模型HMM.
Alice知道这个地区的总的天气趋势,并且平时知道Bob会做的事情.也就是说这个隐马尔可夫模型的参数是已知的.可以用程序语言(Python)写下来:
// 状态数目,两个状态:雨或晴
states = (‘Rainy’, ‘Sunny’)
// 每个状态下可能的观察值
observations = (‘walk’, ‘shop’, ‘clean’)
//初始状态空间的概率分布
start_probability = {‘Rainy’: 0.6, ‘Sunny’: 0.4}
// 与时间无关的状态转移概率矩阵
transition_probability = {
’Rainy’ : {‘Rainy’: 0.7, ‘Sunny’: 0.3},
’Sunny’ : {‘Rainy’: 0.4, ‘Sunny’: 0.6},
}
//给定状态下,观察值概率分布,发射概率
emission_probability = {
’Rainy’ : {‘walk’: 0.1, ‘shop’: 0.4, ‘clean’: 0.5},
’Sunny’ : {‘walk’: 0.6, ‘shop’: 0.3, ‘clean’: 0.1},
}
在这些代码中,start_probability代表了Alice对于Bob第一次给她打电话时的天气情况的不确定性(Alice知道的只是那个地方平均起来下雨多些).在这里,这个特定的概率分布并非平衡的,平衡概率应该接近(在给定变迁概率的情况下){‘Rainy’: 0.571, ‘Sunny’: 0.429}。 transition_probability 表示马尔可夫链下的天气变迁情况,在这个例子中,如果今天下雨,那么明天天晴的概率只有30%.代码emission_probability 表示了Bob每天作某件事的概率.如果下雨,有 50% 的概率他在清理房间;如果天晴,则有60%的概率他在外头散步。
Alice和Bob通了三天电话后发现第一天Bob去散步了,第二天他去购物了,第三天他清理房间了。Alice现在有两个问题:
这个观察序列“散步、购物、清理”的总的概率是多少?(注:这个问题对应于HMM的基本问题之一:已知HMM模型λ及观察序列O,如何计算P(O|λ)?)
最能解释这个观察序列的状态序列(晴/雨)又是什么?(注:这个问题对应HMM基本问题之二:给定观察序列O=O1,O2,…OT以及模型λ,如何选择一个对应的状态序列S = q1,q2,…qT,使得S能够最为合理的解释观察序列O?)
至于HMM的基本问题之三:如何调整模型参数, 使得P(O|λ)最大?这个问题事实上就是给出很多个观察序列值,来训练以上几个参数的问题。
HMM基本算法
1. 对于一个观察序列匹配最可能的系统——评估,使用前向算法(forward algorithm)解决;
2. 对于已生成的一个观察序列,确定最可能的隐藏状态序列——解码,使用Viterbi 算法(Viterbi algorithm)解决;
3. 对于已生成的观察序列,决定最可能的模型参数——学习,使用前向-后向算法(forward-backward algorithm)解决。
前向算法
对于第一个基本问题,计算公式为:

即对于观察序列O,我们需要找出所有可能的隐藏状态序列S,计算出在给定模型下S输出为O的概率(就是样例问题一啊),然后计算概率之和。
直观上看,假如序列O的长度为T,模型的隐藏状态集合大小为N,那么一共有NT个可能的隐藏状态序列,计算复杂度极高O(NT),暴力算法太慢了。
解决方案就是动态规划(Dynamic Programming)。
假设观察序列为O1,O2,O3,….,Ot. 在时刻i(1<i<=t)时,定义C为产生序列O1,O2,…,Oi且Si=Sk的概率:

其中,Sk为任意一个隐藏状态值。
则C(i+1,Or)的计算公式为:

其中,Sr为任意一个隐藏状态值。A为转移概率。B为隐藏状态到观察状态的概率。为了便于理解,还是看图:

C(3,下雨)考虑了t=1和t=2的所有组合情况,同时也是C(4,下雨|阴天|晴天)的子问题。C(3,阴天)和C(3,晴天)也是如此计算,而C(i+1,Sr)计算公式则可以表示成:

由图知:C(4,阴天)=[C(3,下雨)*A(下雨,阴天)+C(3,阴天)*A(阴天,阴天)+C(3,晴天)*A(晴天,阴天)]*B(阴天,自习)。
通过图片,大家应该能直观的理解该算法了,该算法又称为前向算法,那还有后向算法?是的,后向算法就是这个算法倒过来嘛,也是动态规划,这里就不赘述了,有兴趣的看参考文献。另外,这里没有讲解如何初始化概率,也可以去参考文献里查证。
维特比算法
现在,HMM的第一个基本问题解决了,下面开始解决第二个问题,第二个问题又称为解码问题,同样的,暴力算法是计算所有可能性的概率,然后找出拥有最大概率值的隐藏状态序列。与问题一的暴力解决方案类似,复杂度为O(NT)。
那应该用什么方案呢?
毫无疑问,还是动态规划啊!
假设观察序列为O1,O2,O3,….,Ot. 在时刻i(1<i<=t)时,定义D为观察O1,O2,…,Oi且Si=Sk时产生该观察序列的最大概率:
其中,S1,S2,….S(i-1),在此时也已经可以得到,因为它们是子问题啊。

童鞋们有么有看到该公式和上面的前向算法的差异?一个是对子问题求和,一个是对子问题求最大值啊。
当然,对于本问题来说,因为需要求出的是使得观察序列概率最大的隐藏状态的序列,而不是最大概率,所以,在算法计算过程中,还需要记录前一个隐藏状态的值。比如C(4,阴天)的最大值是有子问题C(3,下雨)得来的,那么需要在C(4,阴天)这个节点记录前置状态为下雨。
由于本算法和前向算法只是计算公式的不同,所以参考图是一样的,本算法还可以参考上面算法的图;同样的,解释中没有提到初始化,可以去看参考文献。
本算法又称为维特比算法,维特比是人名,这个老先生在上世纪70年代发明的该算法,但在现代人看来没什么神秘,可见问题在解决后可能会很简单,所以不管是生活上还是学术上都不要畏惧,勇于战而后知战之易矣。
相信理解了前向算法和维特比算法后,大家对样例问题2和样例问题4都能解决了吧,对于样例问题3,其实跟维特比算法差不多,只不过是在观察状态的空间中寻找最优解。
对于基本问题三,待续。
隐马尔科夫过程的应用
HMM一开始是在信息论中应用的,后来才被应用到自然语言处理还有其他图像识别等各个方面。
下面举两个例子说明他的应用,一个是输入法的整句解码,一个是语音识别。有图为证:

输入法把拼音看做是观察状态,需要得到的汉字为隐藏状态,这样,输入法的整句解码就变成了维特比解码,其转移概率即是二元语言模型,其输出概率即是多音字对应不同拼音的概率。
将上图中的拼音换成语音,就成了语音识别问题,转移概率仍然是二元语言模型,其输出概率则是语音模型,即语音和汉字的对应模型。
隐马尔可夫模型的其它应用
基因组序列中蛋白质编码区域的预测
对于相互关联的DNA或蛋白质族的建模
从基本结构中预测第二结构元素
通信中的译码过程
隐马可夫模型在语音处理上的应用
因为马可夫模型有下列特色:
时间点 的隐藏条件和时间点
的隐藏条件和时间点 的隐藏条件有关。因为人类语音拥有前后的关联,可以从语义与发音两点来看:
的隐藏条件有关。因为人类语音拥有前后的关联,可以从语义与发音两点来看:
单字的发音拥有前后关联:例如"They are"常常发音成"They're",或是"Did you"会因为"you"的发音受"did"的影响,常常发音成"did ju",而且语音辨识中用句子的发音来进行分析,因此需要考虑到每个音节的前后关系,才能够有较高的准确率。
句子中的单字有前后关系:从英文文法来看,主词后面常常接助动词或是动词,动词后面接的会是受词或介系词。而或是从单一单字的使用方法来看,对应的动词会有固定使用的介系词或对应名词。因此分析语音讯息时需要为了提升每个单字的准确率,也需要分析前后的单字。
马可夫模型将输入讯息视为一单位一单位,接着进行分析,与人类语音模型的特性相似。语音系统辨识的单位为一个单位时间内的声音。利用梅尔倒频谱等语音处理方法,转换成一个发音单位,为离散型的资讯。而马可夫模型使用的隐藏条件也是一个个被封包的 ,因此使用马可夫模型来处理声音讯号比较合适。
,因此使用马可夫模型来处理声音讯号比较合适。
from:http://blog.csdn.net/pipisorry/article/details/50722178
ref: HiddenMarkovModels*
Lawrence R. Rabiner (February 1989). “A tutorial on Hidden Markov Models and selected applications in speech recognition”
隐马尔科夫模型(Hidden Markov Models)介绍
隐马尔可夫模型的原理及实现 HMM(一)
HMM:隐马尔可夫模型HMM的更多相关文章
- 基于隐马尔科夫模型(HMM)的地图匹配(Map-Matching)算法
文章目录 1. 1. 摘要 2. 2. Map-Matching(MM)问题 3. 3. 隐马尔科夫模型(HMM) 3.1. 3.1. HMM简述 3.2. 3.2. 基于HMM的Map-Matchi ...
- 隐马尔科夫模型HMM学习最佳范例
谷歌路过这个专门介绍HMM及其相关算法的主页:http://rrurl.cn/vAgKhh 里面图文并茂动感十足,写得通俗易懂,可以说是介绍HMM很好的范例了.一个名为52nlp的博主(google ...
- 猪猪的机器学习笔记(十七)隐马尔科夫模型HMM
隐马尔科夫模型HMM 作者:樱花猪 摘要: 本文为七月算法(julyedu.com)12月机器学习第十七次课在线笔记.隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来 ...
- 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(一)HMM模型
隐马尔科夫模型HMM(一)HMM模型基础 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比 ...
- 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数(TODO) 隐马尔科夫模型HMM(四)维特比算法 ...
- 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态序列
隐马尔科夫模型HMM(一)HMM模型 隐马尔科夫模型HMM(二)前向后向算法评估观察序列概率 隐马尔科夫模型HMM(三)鲍姆-韦尔奇算法求解HMM参数 隐马尔科夫模型HMM(四)维特比算法解码隐藏状态 ...
- 用hmmlearn学习隐马尔科夫模型HMM
在之前的HMM系列中,我们对隐马尔科夫模型HMM的原理以及三个问题的求解方法做了总结.本文我们就从实践的角度用Python的hmmlearn库来学习HMM的使用.关于hmmlearn的更多资料在官方文 ...
- 机器学习之隐马尔科夫模型HMM(六)
摘要 隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔科夫过程.其难点是从可观察的参数中确定该过程的隐含参数,然后利用这些参数来作进一步 ...
随机推荐
- Python笔记(一)——打印输出
一.输出语句input 输出语句print 例:用户输入 username = input("username:") #变量名 显示的字符 password = input( ...
- node之querystring模块
前言 querystring 模块提供了一些实用工具,用于解析与格式化 URL 查询字符串. 一.querystring.parse() 用于将一个查询字符串解析为JS 对象. const query ...
- js中一个对象当做参数传递时候?
高程中讲到:'ECMAScript 中所有函数的参数都是按值传递'. 这就像把值从一个变量复制到另一个变量一样. 那引用类型的值也是像基本类型一样? 直接看栗子一: var person = { na ...
- 我在 Ubuntu 下使用 Sublime 编写 python 代码时遇到并解决的问题
Ubuntu 下 Sublime 无法输入中文 解决方法如下: sudo apt-get update && sudo apt-get upgrade 克隆项目到本地 : git cl ...
- 18. 4Sum(中等)
Given an array S of n integers, are there elements a, b, c, and d in S such that a + b + c + d = tar ...
- HashSet<T>的妙用
HashSet<int> hs = new HashSet<int>(); var ret = hs.Add(1); //ret==true var ret2 = hs.Ad ...
- C# 基础问答
1.静态变量和非静态变量的区别? 2.const 和 static readonly 区别? 3.extern 是什么意思? 4.abstract 是什么意思? 5.internal 修饰符起什么作用 ...
- WUOJ-ACM :1003: 零起点学算法78——牛牛
武汉科技大学ACM :1003: 零起点学算法78--牛牛Problem Description牛牛是一种纸牌游戏,总共5张牌,规则如下: 如果找不到3张牌的点数之和是10的倍数,则为没牛: 如果其中 ...
- --save-dev 和 --save的区别
1. 我们在使用npm install xx --save-dev / --save安装模块或插件的时候,会将他们写入到 package.json 文件,那到底有什么区别呢? --save-dev:会 ...
- ubuntu安装fat32和exfat文件系统支持
vftp(fat32) apt install -y dosfstools exfat apt install -y exfat-fuse exfat-utils
