java用Kruskal实现最小生成树

今天更新这篇文章超级激动，因为我会最小生成树的算法了(其实昨天就开始研究了，只是昨天参加牛客网的算法比赛，结果又被虐了，好难过~)

最小生成树的算法，其实学了数据结构就会有一定的基础，Kruskal算法是贪婪法的一种，一直在所有边中选择最小边(当然不能形成环，因为最小生成树是没有环的)。首先遇到的问题就是如何表示这个图，想用邻接矩阵还是关联矩阵。但是这两种矩阵都要输入好多，感觉太浪费空间了。于是，我自己定义了一个类，是边的类。只要一个图的每一条边都关联两个点，两个端点。于是这个类中包括一个关联点的数组，是否被选择，以及边的权值。另外就是这个边的代号，以a,b,c,d...来表示，顶点是int类型,以1,2,3,4...来表示。接下来来看实际的题目吧。

1.问题描述:

　　　　如下图，求图的最小生成树，把边选出来，并且求出最小生成树的权值

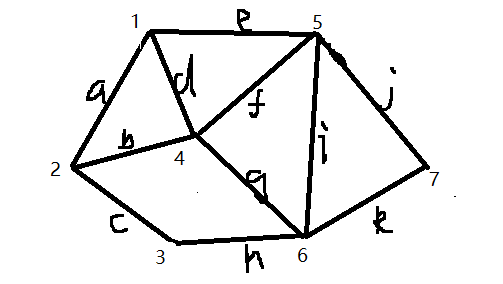
　　　　每条边的权值如下:

　　　　 a -------------4

　　　　 b--------------6

　　　　 c--------------4

　　　　 d--------------2

　　　　 e--------------3

　　　　 f---------------1

　　　 　g--------------2

　　　 　h--------------3

　　　 　i---------------4

　　　 　j---------------1

　　　 　k--------------2

由图利用Kruskal算法不难得出最小生成树所选的边是: f  j  g  d  h  c   / f  j  g  d  h  c....

2.输入:请输入这个图有几条边和顶点数:(11表示边条数，7表示顶点个数) ，接下来3个数，分别为边的权值，边和哪两个点关联
　　　　11 7 
　　　　4 1 2
　　　　6 2 4
　　　　4 2 3
　　　　2 1 4
　　　　3 1 5
　　　　1 4 5
　　　　2 4 6
　　　　3 3 6
　　　　4 5 6
　　　　1 5 7
　　　　2 6 7

3.输出:

　　　　选的边为: f j g d h c
　　　　权值是:13
4.算法思想:

　　　　输入完了之后用一个排序方法，将树的权值从小到大进行排序，保存在Bian[]这个数组中。接下来再从小到大进行选择，判断是否不在同一个连通分量和没有被选择。判断不在一个连通分量很关键。这个思想，我昨天想了好久，开始是想选的边不能形成圈，但发现这样也太难判断了，该怎么看是否形成圈呢？然后就各种百度，查资料，然后发现只要不在同一个联通分量就可以了。比如假如上图:我边a权值是1，边j权值是1，如果不在同一个连通分量，那么还是可以选择的。化为计算机语言，也就是我把已经选择了的边的顶点保存在一个顶点数组里面，如果我接下来要添加的边的两个端点都已经在在这个数组里面，那么就不能选了，如果有一个在，一个不在，或者两个都不在，就可以选。仔细想想是不是这个道理呢？但是我这样做之后发现程序总是少选1条边，原来，选到只剩最后一条边的时候，是可能会两个端点都在数组里的(当然有些图也不会)，于是在最后一条边时需要另外判断了。如果是最后一条边，并且两个点都在的话，那就选这条边，else if 继续前面那种选法就可以。

5.代码示例:

import java.util.Scanner;

class Edge{
    int v; //边的权值
    int[] ConnectPoint = new int[2];  //边所连接的点
    int isSelect; //是否被选择，1表示被选，0表示没有被选
    char No; //图的编号,a,b,c,d...在创建图的时候初始化的
}

public class 最小生成树2 {
    public static void main(String[] args) {
        Scanner scn = new Scanner(System.in);
        System.out.println("请输入图有几条边和几个点:");
        int n = scn.nextInt();  //保存边数
        int m = scn.nextInt(); //保存点数
        Edge edge[] = new Edge[n];
        for(int i=0;i<n;i++){
            edge[i] = new Edge();  //创建出真实的边出来
            edge[i].v = scn.nextInt();
            edge[i].ConnectPoint[0] = scn.nextInt();
            edge[i].ConnectPoint[1] = scn.nextInt();
            edge[i].No = (char) ('a' + i);
        }
        
        //输入完了之后，将这些边按权值进行排序
        sort(edge);
        
        //定义一个点的数组，来存放已经选择的边的关联顶点编号
        int hasSelectPoint[] = new int[2*m];  //因为每条边都有关联两个顶点,选择的边存放进来可能会存放两次
        //初始化，这个数组开始全部存0，都没有被选择
        for(int i=0;i<hasSelectPoint.length;i++){
            hasSelectPoint[i] = 0;
        }
        
        //权值排序完成之后就开始选边
        int j=0;
        int step = 1;//选的边数，开始选第一条边
        for(int i=0;i<n;i++){
            //最小生成树要选的边数等于顶点数-1,那么开始要选m-1最后一条边时这样选。再break退出
            if(step == m-1 && allInSelectPoint(edge[i],hasSelectPoint)){ //最后一条边了
                    edge[i].isSelect = 1;//直接选择
                    break;
            }else if(edge[i].isSelect ==0 && !allInSelectPoint(edge[i],hasSelectPoint)){ //如果边没有被选，并且这条边的两个顶点不同时在顶点的数组里
                    edge[i].isSelect = 1;
                    hasSelectPoint[j] = edge[i].ConnectPoint[0];
                    j++;
                    hasSelectPoint[j] = edge[i].ConnectPoint[1];
                    j++;
                    step++; //开始选第二条边
            }
        }
        
        //打印所选的边
        int sum = 0; // 计算权值
        System.out.print("所选的边为:");
        for(int i=0;i<n;i++){
            if(edge[i].isSelect==1){
                sum = sum + edge[i].v;
                System.out.print(edge[i].No + " ");
            }
        }
        System.out.println();
        System.out.println("权值为: " + sum);
    }

    private static boolean allInSelectPoint(Edge edge, int[] hasSelectPoint) {
        int flag1 = 0;
        int flag2 = 0;//这两个变量是分别看边的两个端点在不在存放已经选择点的数组里面
        for(int i=0;i<hasSelectPoint.length;i++){
            if(edge.ConnectPoint[0] ==hasSelectPoint[i]){
                flag1 = 1;
            }
            if(edge.ConnectPoint[1] ==hasSelectPoint[i]){
                flag2 = 1;
            }
        }
        if(flag1 ==1 && flag2 ==1){  //两个点都在
            return true;
        }else {  //都不在或者有一个点不在
            return false;
        }
    }

    //将权值进行交换
    private static void sort(Edge[] edge) {
        Edge tempEdge = null;
        for(int i=0;i<edge.length;i++){
            for(int j=i+1;j<edge.length;j++){
                if(edge[j].v<edge[i].v){
                    tempEdge = edge[i];
                    edge[i] = edge[j];
                    edge[j] = tempEdge;
                }
            }
        }
    }
}