class-提升方法Boosting
2 AdaBoost训练误差分析
3 AdaBoost algorithm 另外的解释
3.1 前向分步算法
3.2 前向分步算法与AdaBoost
4 提升树
4.1 提升树模型
4.2 梯度提升
Boosting在分类问题中,通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类性能。AdaBoost最具代表性,由Freund和Schapire在1995年提出;Boost树在2000年由Friedman提出。
1 AdaBoost算法
基本思想:对于分类而言,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)比强分类器容易得多。因此此方法就是从弱分类器出发,反复学习,得到一系列弱分类器(基本分类器),然后组合成一个强分类器。Boosting方法大多是改变训练数据的权值分布,针对不同训练数据分布调用弱分类器进行一系列学习的方法。如何改变训练数据的权值或概率分布?提高前一轮弱分类器错误分类的样本的权值,而降低正确分类样本的权值,这样错误分类的样本在本次弱分类器中就被更大的关注,一次分类问题就被一系列分类器分而治之。如何组合这一组弱分类器?——加权多数表决的方法,加大无误差率低的弱分类器的权值,减小误差率大的弱分类器的权值,让其在表决中起较小作用。
算法:


说明:
步骤一中,权值分布采取均匀分布得到权值向量D1,在原始数据上学习分类器;
步骤二中,m表示轮数,m=1表示第一轮学习过程。
(a)使用当前权值向量Dm加权训练集,学习基本分类器Gm(x)。
(b)计算基本分类器在加权训练集上的误分类率em,可以看出Gm(x)的分类误差率是误分类样本权重之和。
(c) Gm的系数就是在最终组合分类器所占的权重,表示此分类器的重要性。em小于1/2时,alpham>=0,随着误分类率的减小而增大,所以误分类率越小的基本分类器在最终分类器所起的作用越大。
(d)中更新权值分布,为下一轮做准备,其实yGm相乘是验证此个样本值分类的正确性,正确则同号,同号则为正,为正则指数部分为负数,就减少此样本值的分量,减少的多少由alpha决定。即
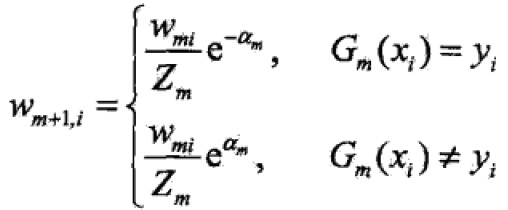
步骤三中,f(x)的线性组合实现了M个基本分类器的加权表决,系数alpha是基本分类器的重要性。注意这里的alpha之和不为1。f(x)的符号表示实例的类别,绝对值的大小表示分类的确信度。最终sign得到强分类器G(x)。
在具体执行过程中,可以每次都进行组合然后得到误分类点,直到误分类点为0为止或者达到m的最大值M为止。
2 AdaBoost训练误差分析
定理:训练误差的界:
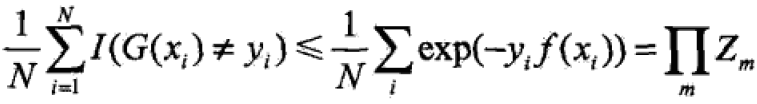
证明:

定理:二类分类的AdaBoost训练误差界:
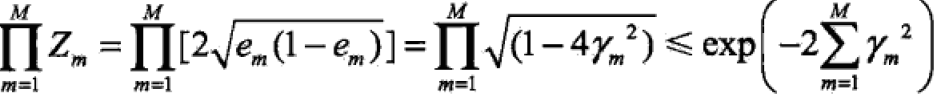 ,
,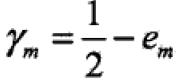
证明:
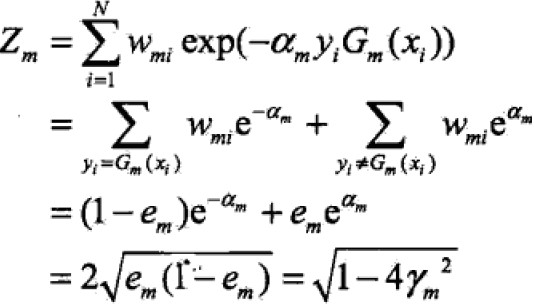

推论:
 表明AdaBoost误差界以指数速率下降。
表明AdaBoost误差界以指数速率下降。
注意:AdaBoost算法不需要知道下界γ,具有适应性adaptive Boosting
3 AdaBoost algorithm 另外的解释
这个解释是AdaBoost算法模型是加法模型,损失函数是指数函数,学习算法为前向分步算法时的二类分类学习方法。
3.1 前向分步算法
加法模型(additive model)
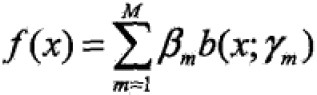
其中,b为基函数,γ为基函数的参数;β为基函数的系数;
给定训练集和损失函数L(y,f(x))条件下,学习加法模型f成为风险极小化或损失函数极小化的问题:
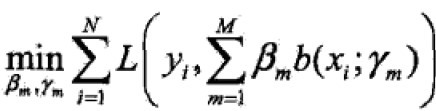
前向分步算法(forward stagewise algorithm)求解思路是:因为学习的模型是加法模型,如果能够从前向后,每一步只学习一个基函数及其系数,逐步逼近优化函数目标(上式),那么就可以简化优化的复杂度。因此,每步只需优化如下损失函数:
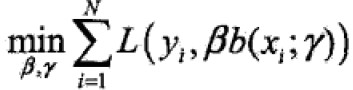
算法明细:

3.2 前向分步算法与AdaBoost
定理:AdaBoost算法是前向分步算法的特例,model为基本分类器组成的加法模型,损失函数是指数函数。
证明:根据算法流程对比二者并无区别,需要注意的是前向分步算法的损失函数是指数损失函数(exponential loss function)
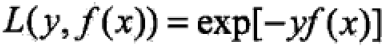

4 提升树
Boosting Tree被认为是统计学习中性能最好的方法之一,以分类树或回归树为基本分类器的提升方法。
4.1 提升树模型
提升方法实际上采用的是加法模型(基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树。对分类问题的决策树是二叉分类树,对回归问题的决策树是二叉回归树。基本分类器xv可以看做由一个根结点直接连接两个叶子结点的简单决策树,即决策树桩(decision stump)。提升树模型可以表示为决策树的加法模型:
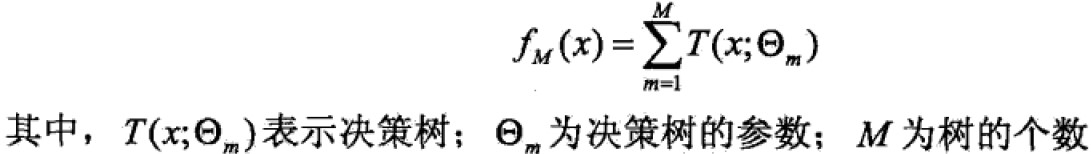
提升算法采用前向分步算法,首先确定初始提升树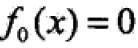 ,则第m步的模型是
,则第m步的模型是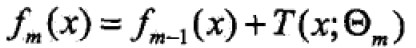 ;
;
经验最小化函数: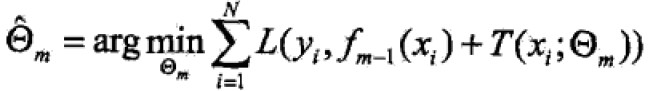 ,m-1表示当前树,经验最小化函数可以确定下一个树的决策参数。
,m-1表示当前树,经验最小化函数可以确定下一个树的决策参数。
不同问题的提升树学习算法,主要区别是使用的损失函数不同(回归问题:平方误差损失函数;分类问题指数损失函数)。
回归问题
已知训练集T={(x1,x2),…(xN,yN)},x属于Rn,y属于R,如果将输入空间划分为J个互不相交的区域R1,…,RJ,并且在每个区域上确定输出常量cj,树可表示为
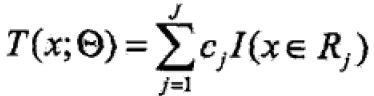
其中,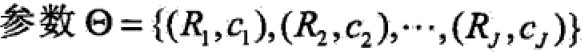 表示树的区域划分和各区域上常数(类)。J是回归树的复杂度即叶子结点个数。
表示树的区域划分和各区域上常数(类)。J是回归树的复杂度即叶子结点个数。
回归提升树使用前向分步算法:
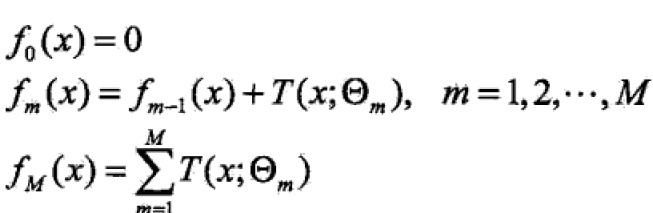
前向分步算法第m步,给定当前模型fm-1,需求: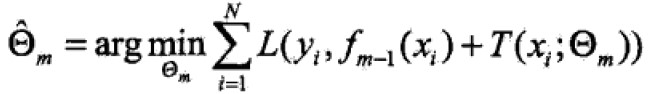 。
。
当采用平方误差损失函数时, 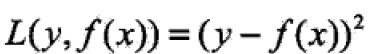
代入得:
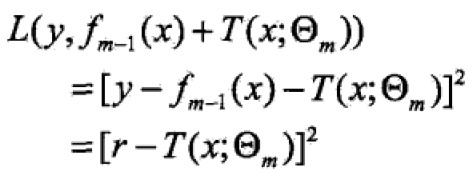
这里,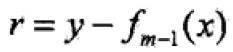 是当前模型拟合数据的残差(residual)
是当前模型拟合数据的残差(residual)
回归树算法:

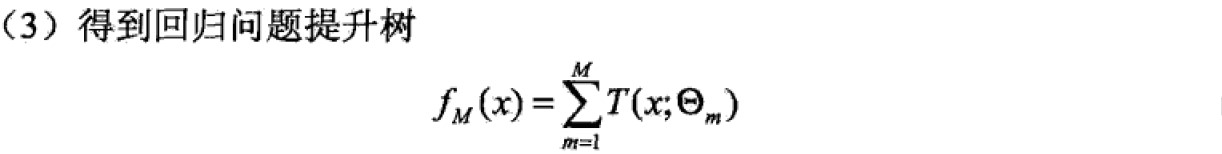
4.2 梯度提升
当损失函数不是平方误差函数或者指数函数时,优化并不简单,故提出梯度提升(gradient Boosting)算法,关键是利用损失函数的负梯度在当前模型的值
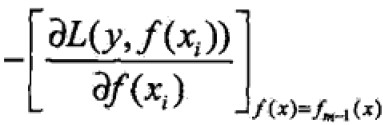 作为回归问题中残差的近似值拟合回归树。
作为回归问题中残差的近似值拟合回归树。
梯度提升算法:

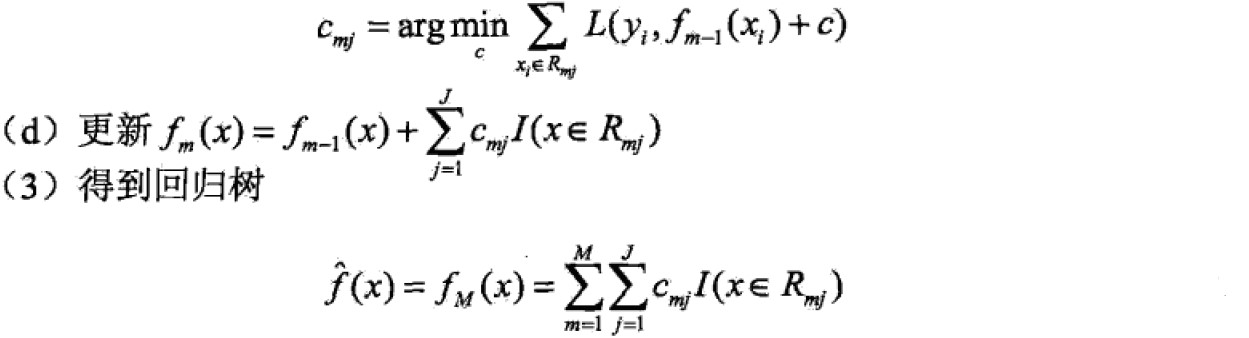
class-提升方法Boosting的更多相关文章
- 提升方法(boosting)详解
提升方法(boosting)详解 提升方法(boosting)是一种常用的统计学习方法,应用广泛且有效.在分类问题中,它通过改变训练样本的权重,学习多个分类器,并将这些分类器进行线性组合,提高分类的性 ...
- Boosting(提升方法)之GBDT
一.GBDT的通俗理解 提升方法采用的是加法模型和前向分步算法来解决分类和回归问题,而以决策树作为基函数的提升方法称为提升树(boosting tree).GBDT(Gradient Boosting ...
- Boosting(提升方法)之AdaBoost
集成学习(ensemble learning)通过构建并结合多个个体学习器来完成学习任务,也被称为基于委员会的学习. 集成学习构建多个个体学习器时分两种情况:一种情况是所有的个体学习器都是同一种类型的 ...
- 组合方法(ensemble method) 与adaboost提升方法
组合方法: 我们分类中用到非常多经典分类算法如:SVM.logistic 等,我们非常自然的想到一个方法.我们是否可以整合多个算法优势到解决某一个特定分类问题中去,答案是肯定的! 通过聚合多个分类器的 ...
- js 变量提升+方法提升
<!DOCTYPE html> <html> <head lang="en"> <meta charset="UTF-8&quo ...
- 机器学习理论提升方法AdaBoost算法第一卷
AdaBoost算法内容来自<统计学习与方法>李航,<机器学习>周志华,以及<机器学习实战>Peter HarringTon,相互学习,不足之处请大家多多指教! 提 ...
- 统计学习方法c++实现之七 提升方法--AdaBoost
提升方法--AdaBoost 前言 AdaBoost是最经典的提升方法,所谓的提升方法就是一系列弱分类器(分类效果只比随机预测好一点)经过组合提升最后的预测效果.而AdaBoost提升方法是在每次训练 ...
- 提升方法-AdaBoost
提升方法通过改变训练样本的权重,学习多个分类器(弱分类器/基分类器)并将这些分类器进行线性组合,提高分类的性能. AdaBoost算法的特点是不改变所给的训练数据,而不断改变训练数据权值的分布,使得训 ...
- 机器学习——提升方法AdaBoost算法,推导过程
0提升的基本方法 对于分类的问题,给定一个训练样本集,求比较粗糙的分类规则(弱分类器)要比求精确的分类的分类规则(强分类器)容易的多.提升的方法就是从弱分类器算法出发,反复学习,得到一系列弱分类器(又 ...
随机推荐
- 关于ES6 用箭头函数后的 this 指向问题
最近写完小程序后, 开始学习React, 因为有编译器, 就直接用ES6 新语法了, 中间自然离不开 () => { console.log('箭头函数的this是指向哪的问题')}; var ...
- 2018/1/28 RocketMq学习笔记
RocketMq是支持Topic模式的MQ中间件,它的传输格式为topic(主题,一个product对应一个主题,),Tag(标签,其实就是副标题,是为了更好的支持集群模式而出现的,这样客户端可以指定 ...
- 怎么理解np.random.seed()?
在使用numpy时,难免会用到随机数生成器.我一直对np.random.seed(),随机数种子搞不懂.很多博客也就粗略的说,利用随机数种子,每次生成的随机数相同. 我有两个疑惑:1, 利用随机数种子 ...
- javascript 一些特殊的字符运算
1.什么是 --> ? 这两个分开是很简单的两个运算符,比如--,一般表示自减,var i = 5;while(i){console.log(i--);},会打印出5,4,3,2,1: > ...
- ASP.NET Core的身份认证框架IdentityServer4--(4)添加第三方快捷登录
添加对外部认证的支持 接下来我们将添加对外部认证的支持.这非常简单,因为你真正需要的是一个兼容ASP.NET Core的认证处理程序. ASP.NET Core本身也支持Google,Facebook ...
- 读《Linux Shell脚本攻略》(第2版) 总结
前段时间读完了<Linux Shell脚本攻略>(第2版)这本书,给部分想读这本书的人分享下个人感受. 说下这本书的难度吧.纯新手或者只懂少部分编程知识的人,读起来还是有很大难度的.以我为 ...
- 每个前端开发者必会的 20 个 JavaScript 面试题
JavaScript 未声明变量直接使用会抛出异常:var name is not defined,如果没有处理异常,代码就停止运行了.但是,使用typeof undeclared_variable并 ...
- SpringMvc笔记-对RESTFUL风格的配置
1.@RequestMapping注解可以使用如下参数: 1,params:例如params={'username',"age!=100"}表示需要usernmame并且age 属 ...
- 端到端测试工具--testcafe
写在前面 随着业务的增加,复杂性的增加,我们更需要保证页面不能出错,之前需要每次上线之前需要每次人工测试,如果有好多改动,为保证业务不出错,需要耗费更多的时间来测试,所以我们需要写一些测试来保证业务的 ...
- python——Django项目模板
views.py # -*- coding: utf-8 -*- from __future__ import unicode_literals from django.shortcuts impor ...
