[NOIP2014]寻找道路（图论）

题目描述

在有向图G 中，每条边的长度均为1 ，现给定起点和终点，请你在图中找一条从起点到终点的路径，该路径满足以下条件：

1 ．路径上的所有点的出边所指向的点都直接或间接与终点连通。

2 ．在满足条件1 的情况下使路径最短。

注意：图G 中可能存在重边和自环，题目保证终点没有出边。

请你输出符合条件的路径的长度。

输入输出格式

输入格式：

输入文件名为road .in。

第一行有两个用一个空格隔开的整数n 和m ，表示图有n 个点和m 条边。

接下来的m 行每行2 个整数x 、y ，之间用一个空格隔开，表示有一条边从点x 指向点y 。

最后一行有两个用一个空格隔开的整数s 、t ，表示起点为s ，终点为t 。

输出格式：

输出文件名为road .out 。

输出只有一行，包含一个整数，表示满足题目᧿述的最短路径的长度。如果这样的路径不存在，输出- 1 。

输入输出样例

输入样例#1：

3 2
1 2
2 1
1 3

输出样例#1：

-1

输入样例#2：

6 6
1 2
1 3
2 6
2 5
4 5
3 4
1 5

输出样例#2：

3

说明

解释1：

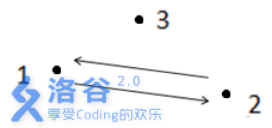
如上图所示，箭头表示有向道路，圆点表示城市。起点1 与终点3 不连通，所以满足题

目᧿述的路径不存在，故输出- 1 。

解释2：

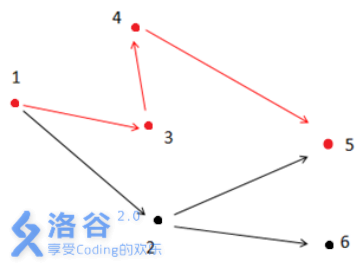
如上图所示，满足条件的路径为1 - >3- >4- >5。注意点2 不能在答案路径中，因为点2连了一条边到点6 ，而点6 不与终点5 连通。

对于30%的数据，0<n≤10，0<m≤20；

对于60%的数据，0<n≤100，0<m≤2000；

对于100%的数据，0<n≤10,000，0<m≤200,000，0<x，y，s，t≤n，x≠t。

• noip2014 day2t2，图论题，不过貌似比较简单。
• 已知只有所有出边都直接或间接指向终点的点才可能被选择，所以就建反边，从终点想起点扫，dfs，bfs均可，在把所有终点不能达到的点打上标记，这些点均不可备选择，并且在反边图中这些点所指向的点也不能被选择（因为在正边图中这些点指向标记点）。因此可以删去图中不符合要求的点，然后跑最短路即可。
• spfa，heap+dijkstra均可，bfs,dfs复杂度为O(n)，spfa复杂度为O(ke)，heap+dijkstra复杂度为O(nloge)，均可通过该题。

 #include <cstdio>
 #include <algorithm>
 #include <cstring>
 using namespace std;

 int tot,total,n,m,ss,tt,l[],r[],pre[],last[],other[];
 int que[],d[];
 bool judge[],vis[],point[];

 void add(int u,int v) {
     pre[++tot]=last[u];
     last[u]=tot;
     other[tot]=v;
 }

 void bfs(int x) {
     int h=,t=;
     que[]=x;
     vis[x]=;
     point[x]=;
     total++;
     while (h<t) {
         int cur=que[++h];
         for (int p=last[cur]; p; p=pre[p]) {
             int q=other[p];
             if (!vis[q]) {
                 vis[q]=;
                 que[++t]=q;
                 total++;
                 point[q]=;
             }
         }
     }
 }

 void spfa(int x) {
     int h=,t=;
     que[]=x;
     memset(d,,sizeof d);
     d[x]=;
     while (h<t) {
         int cur=que[++h];
         vis[cur]=;
         for (int p=last[cur]; p; p=pre[p]) {
             int q=other[p];
             if (!point[q]) continue;
             if (judge[q]) continue;
             if (d[q]>d[cur]+) {
                 d[q]=d[cur]+;
                 if (!vis[q]) {
                     vis[q]=;
                     que[++t]=q;
                 }
             }
         }
     }
 }

 int main() {
     scanf("%d%d",&n,&m);
     for (int i=; i<=m; i++) scanf("%d%d",&l[i],&r[i]);
     scanf("%d%d",&ss,&tt);
     for (int i=; i<=m; i++) add(r[i],l[i]);
     bfs(tt);
     if (!point[ss]) {
         printf("%d",-);
         return ;
     }
     for (int i=; i<=n; i++) {
         if (point[i]) continue;
         for (int p=last[i]; p; p=pre[p]) {
             int q=other[p];
             judge[q]=;
         }
     }
     memset(que,,sizeof que);
     memset(vis,,sizeof vis);
     memset(last,,sizeof last);
     tot=;
     for (int i=; i<=m; i++) add(l[i],r[i]);
     spfa(ss);
     printf("%d",d[tt]);
     return ;
 }