893E - Counting Arrays

E. Counting Arrays

time limit per test

3 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given two positive integer numbers x and y. An array F is called an y-factorization of x iff the following conditions are met:

• There are y elements in F, and all of them are integer numbers;
• .

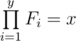You have to count the number of pairwise distinct arrays that are y-factorizations of x. Two arrays A and B are considered different iff there exists at least one index i (1 ≤ i ≤ y) such that Ai ≠ Bi. Since the answer can be very large, print it modulo 109 + 7.

Input

The first line contains one integer q (1 ≤ q ≤ 105) — the number of testcases to solve.

Then q lines follow, each containing two integers xi and yi (1 ≤ xi, yi ≤ 106). Each of these lines represents a testcase.

Output

Print q integers. i-th integer has to be equal to the number of yi-factorizations of xi modulo 109 + 7.

Example

input

2
6 3
4 2

output

36
6

Note

In the second testcase of the example there are six y-factorizations:

• { - 4,  - 1};
• { - 2,  - 2};
• { - 1,  - 4};
• {1, 4};
• {2, 2};
• {4, 1}.

题意：给出x,y。求满足含有y个元素的之积是x的数列个数。

思路：排列组合，插空法。

代码：

 #include<bits/stdc++.h>
 #define db double
 #define ll long long
 #define vec vector<ll>
 #define Mt  vector<vec>
 #define ci(x) scanf("%d",&x)
 #define cd(x) scanf("%lf",&x)
 #define cl(x) scanf("%lld",&x)
 #define pi(x) printf("%d\n",x)
 #define pd(x) printf("%f\n",x)
 #define pl(x) printf("%lld\n",x)
 #define rep(i,x,y) for(int i=x;i<=y;i++)
 #define debug puts("-------------");
 const int N = 1e6 + ;
 const int mod = 1e9 + ;
 const int MOD = mod-;
 const db  eps = 1e-;
 const db  PI = acos(-1.0);
 using namespace std;
 bool v[N];
 int pri[N];
 ll F[N], Finv[N], inv[N];//F是阶乘，Finv是逆元的阶乘
 
 int p=;
 void init()
 {
     memset(v,,sizeof(v));
     for(int i=;i<;i++){
         if(!v[i]) pri[p++]=i;
         for(int j=*i;j<;j+=i) {v[j]=;}
     }
     inv[] = ;
     for(int i = ; i < ; i ++){
         inv[i] = (mod - mod / i) * 1ll * inv[mod % i] % mod;
     }
     F[] = Finv[] = ;
     for(int i = ; i < ; i ++){
         F[i] = F[i-] * 1ll * i % mod;
         Finv[i] = Finv[i-] * 1ll* inv[i] % mod;
     }
 }
 ll C(ll n, ll m){    //comb(n, m)就是C(n, m)
     if(m <  || m > n)  return ;
     return F[n] * 1ll * Finv[n - m] % mod * Finv[m] % mod;
 }
 ll qpow(ll x,ll n)
 {
     ll ans=;
     x%=mod;
     while(n){
         if(n&) ans=ans*x%mod;
         x=x*x%mod;
         n>>=;
     }
     return  ans;
 }
 
 int main(){
     int q;
     ci(q);
     init();
     for(int i=;i<q;i++)
     {
         ll x,y;
         cl(x),cl(y);
         ll ans=qpow(,y-);
         if(x==){
             pl(qpow(, y - ));
             continue;
         }
         vector<int> e;e.clear();
         map<int,int> mp;mp.clear();
         int id=;
         while(x>){
             if(x%pri[id]==){
                 int n=;
                 while(x%pri[id]==) n++,x/=pri[id];
                 ans=ans*C(n+y-,y-)%mod;
             }
             id++;
             if(pri[id]>){
                 if(x>) ans=ans*y%mod;
                 break;
             }
         }
         pl(ans);
     }
     return ;
 }