2016 Noip提高组

2557. [NOIP2016]天天爱跑步

★★☆   输入文件：runninga.in   输出文件：runninga.out   简单对比
时间限制：2 s   内存限制：512 MB

【题目描述】

小C同学认为跑步非常有趣，于是决定制作一款叫做《天天爱跑步》的游戏。《天天爱跑步》是一个养成类游戏，需要玩家每天按时上线，完成打卡任务。

这个游戏的地图可以看作一棵包含n个结点和n-1条边的树，每条边连接两个结点，且任意两个结点存在一条路径互相可达。树上结点编号为从1到n的连续正整数。

现在有m个玩家，第i个玩家的起点为Si，终点为Ti。每天打卡任务开始时，所有玩家在第0秒同时从自己的起点出发，以每秒跑一条边的速度，不间断地沿着最短路径向着自己的终点跑去，跑到终点后该玩家就算完成了打卡任务。（由于地图是一棵树，所以每个人的路径是唯一的）

小C想知道游戏的活跃度, 所以在每个结点上都放置了一个观察员。 在结点的观察员会选择在第Wj秒观察玩家, 一个玩家能被这个观察员观察到当且仅当该玩家在第Wj秒也理到达了结点J  。 小C想知道每个观察员会观察到多少人?

注意: 我们认为一个玩家到达自己的终点后该玩家就会结束游戏, 他不能等待一 段时间后再被观察员观察到。 即对于把结点J作为终点的玩家: 若他在第Wj秒重到达终点,则在结点J的观察员不能观察到该玩家;若他正好在第Wj秒到达终点,则在结点的观察员可以观察到这个玩家。

【输入格式】

第一行有两个整数n和m。其中n代表树的结点数量，同时也是观察员的数量，m代表玩家的数量。

接下来n-1行每行两个整数u和v，表示结点u到结点v有一条边。

接下来一行n个整数，其中第j个整数为Wj，表示结点j出现观察员的时间。

接下来m行,每行两个整数Si和Ti，表示一个玩家的起点和终点。

对于所有的数据，保证1≤Si,Ti≤n，0≤ Wj ≤n。

【输出格式】

输出1行n个整数,第j个整数表示结点j的观察员可以观察到多少人。

【样例1输入】

6 3
2 3
1 2
1 4
4 5
4 6
0 2 5 1 2 3
1 5
1 3
2 6

【样例1输出】

2 0 0 1 1 1

【样例2输入】

5 3

1 2

2 3

2 4

1 5

0 1 0 3 0

3 1

1 4

5 5

【样例2输出】

1 2 1 0 1

【提示】

对于1号点，W1=0，故只有起点为1号点的玩家才会被观察到，所以玩家1和玩家2被观察到，共2人被观察到。

对于2号点，没有玩家在第2秒时在此结点，共0人被观察到。

对于3号点，没有玩家在第5秒时在此结点，共0人被观察到。

对于4号点，玩家1被观察到，共1人被观察到。

对于5号点，玩家2被观察到，共1人被观察到。

对于6号点，玩家3被观察到，共1人被观察到。

如果你的程序需要用到较大的栈空间(这通常意味着需要较深层数的递归)，请务必仔细阅读选手目录下的文档running/stackpdf，以了解在最终评测时栈空间的限制与在当前工作环境下调整栈空间限制的方法。

感觉没脸见人了

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
using namespace std;
const int maxn=;
int head[maxn*],num,n,m,w[maxn],s[maxn],t[maxn],ans[maxn],fa[maxn];
int dep[maxn],sz[maxn],top[maxn],son[maxn];
bool flag1_2=,flag3_4=,flag6_8=,flag9_12=,flag13_16=;
struct node{
    int to,pre;
}e[maxn*];
void Insert(int from,int to){
    e[++num].to=to;
    e[num].pre=head[from];
    head[from]=num;
}
void dfs1(int now,int father){
    fa[now]=father;
    dep[now]=dep[father]+;
    sz[now]=;
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==father)continue;
        dfs1(to,now);
        sz[now]+=sz[to];
        if(sz[son[now]]<sz[to]||!son[now])son[now]=to;
    }
}
void dfs2(int now,int father){
    top[now]=father;
    if(son[now])dfs2(son[now],father);
    for(int i=head[now];i;i=e[i].pre){
        int to=e[i].to;
        if(to==fa[now]||to==son[now])continue;
        dfs2(to,to);
    }
}
int LCA(int a,int b){
    while(top[a]!=top[b]){
        if(dep[top[a]]<dep[top[b]])swap(a,b);
        a=fa[top[a]];
    }
    if(dep[a]>dep[b])swap(a,b);
    return a;
}
void work1(){//1~2 所有人的起点等于自己的终点
    for(int i=;i<=m;i++)if(w[s[i]]==)ans[s[i]]++;
    for(int i=;i<=n;i++)printf("%d ",ans[i]);
}
void work2(){//3~4 w[]=0
    for(int i=;i<=m;i++)ans[s[i]]++;
    for(int i=;i<=n;i++)printf("%d ",ans[i]);
}
void work3(){//6~8 树退化成一条链
    int block;
    for(int i=;i<=m;i++){
        int step=abs(s[i]-t[i]);
        if(s[i]>t[i])block=-;
        else block=;
        for(int j=,k=s[i];j<=step;j++,k+=block)
            if(w[k]==j)ans[k]++;
    }
    for(int i=;i<=n;i++)printf("%d ",ans[i]);
}
void work4(){//9~12 s[]=1
    dfs1(,);//处理父亲节点
    for(int i=;i<=m;i++){
        int step=dep[t[i]]-dep[s[i]];
        for(int j=step,k=t[i];j>=;j--,k=fa[k])
            if(w[k]==j)ans[k]++;
    }
    for(int i=;i<=n;i++)printf("%d ",ans[i]);
}
void work5(){//13~16 t[]=1
    dfs1(,);
    for(int i=;i<=m;i++){
        int step=dep[s[i]]-dep[t[i]];
        for(int j=,k=s[i];j<=step;j++,k=fa[k])
            if(w[k]==j)ans[k]++;
    }
    for(int i=;i<=n;i++)printf("%d ",ans[i]);
}
void work6(){
    dfs1(,);
    dfs2(,);
    for(int i=;i<=m;i++){
        int lca=LCA(s[i],t[i]);
        int step=abs(dep[s[i]]-dep[lca]);
        for(int j=,k=s[i];j<=step;j++,k=fa[k])
            if(w[k]==j)ans[k]++;
        step++;
        int end=abs(dep[t[i]]-dep[lca]+step-);
        for(int j=end,k=t[i];j>=step;j--,k=fa[k])
            if(w[k]==j)ans[k]++;
    }
    for(int i=;i<=n;i++)printf("%d ",ans[i]);
}
int main(){
    //freopen("Cola.txt","r",stdin);
    freopen("runninga.in","r",stdin);
    freopen("runninga.out","w",stdout);
    scanf("%d%d",&n,&m);
    int x,y;
    for(int i=;i<n;i++){
        scanf("%d%d",&x,&y);
        Insert(x,y);
        Insert(y,x);
        if(abs(x-y)!=)flag6_8=;
    }
    for(int i=;i<=n;i++){
        scanf("%d",&w[i]);
        if(w[i])flag3_4=;
    }
    for(int i=;i<=m;i++){
        scanf("%d%d",&s[i],&t[i]);
        if(s[i]!=t[i])flag1_2=;
        if(s[i]!=)flag9_12=;
        if(t[i]!=)flag13_16=;
    }
    if(flag1_2){work1();return ;}
    if(flag3_4){work2();return ;}
    if(flag6_8){work3();return ;}
    if(flag9_12){work4();return ;}
    if(flag13_16){work5();return ;}
    work6();
    return ;
}

25分 暴力

P1850 换教室

【题目描述】

对于刚上大学的牛牛来说, 他面临的第一个问题是如何根据实际情况中情合适的课程。

在可以选择的课程中,有2n节课程安排在n个时间段上。在第 i ( 1≤ i≤n)个时同段上, 两节内容相同的课程同时在不同的地点进行, 其中, 牛牛预先被安排在教室 ci上课, 而另一节课程在教室 di进行。

在不提交任何申请的情况下,学生们需要按时间段的顺序依次完成所有的n节安排好的课程。如果学生想更换第i节课程的教室,则需要提出中情。若申请通过,学生就可以在第 i个时间段去教室 di上课, 否则仍然在教室 ci上课。

由于更换教室的需求太多, 申请不一定能获得通过。 通过计算, 牛牛发现申请更换第 i节课程的教室时, 中情被通过的概率是一个已知的实数 ki, 并且对于不同课程的申请, 被通过的概率是互相独立的。

学校规定, 所有的申请只能在学期开始前一次性提交, 并且每个人只能选择至多m节课程进行申请。 这意味着牛牛必须一次性决定是否申请更换每节课的教室, 而不能根据某些课程的申请结果来决定其他课程是否申请; 牛牛可以申请白己最希望更换教室的 m门课程,也可以不用完这m个中情的机会,甚至可以一门课程都不申请。

因为不同的课程可能会被安排在不同的教室进行, 所以牛牛需要利用课问时间从一间教室赶到另一间教室。

牛牛所在的大学有 v个教室,有 e条道路。每条道路连接两间教室, 并且是可以双向通行的。 由于道路的长度和拥;i者程度不同, 通过不同的道路耗费的体力可能会有所不同。当第i ( 1≤i≤n-1 )节课结束后,牛牛就会从这节课的教室出发,选择一条耗费体力最少的路径前往下一节课的教室。

现在牛牛想知道,申请哪几门课程可以使他因在教室问移动耗费的体力值的总和的期望值最小,请你帮他求出这个最小值。

【输入输出格式】

输入格式：

第一行四个整数 n,m,v,e 。 n表示这个学期内的时间段的数量; m表示牛牛最多可以申请更换多少节课程的教室; v表示牛牛学校里教室的数量; e表示牛牛的学校里道路的数量。

第二行n个正整数,第 i ( 1≤ i≤ n)个正整数表示c,,即第 i个时间段牛牛被安排上课的教室;保证1≤ ci≤ v。

第三行n个正整数,第 i ( 1≤ i≤ n)个正整数表示di,即第 i个时间段另一间上同样课程的教室;保证1≤ di≤ v。

第四行n个实数,第 i ( 1≤ i≤ n)个实数表示ki,即牛牛申请在第 i个时间段更换教室获得通过的概率。保证0≤ ki≤1 。

接下来 e行,每行三个正整数aj,bj,wj,表示有一条双向道路连接教室 aj ,bj ,通过这条道路需要耗费的体力值是 Wj ;保证1≤ aj,bj≤ v, 1≤ wj≤100 。

保证1≤n≤2000, 0≤m≤2000, 1≤v≤300, 0≤ e≤90000。

保证通过学校里的道路,从任何一间教室出发,都能到达其他所有的教室。

保证输入的实数最多包含3位小数。

输出格式：

输出一行,包含一个实数,四舎五入精确到小数点后恰好2位,表示答案。你的

输出必须和标准输出完全一样才算正确。

测试数据保证四舎五入后的答案和准确答案的差的绝对值不大于4 *10^-3 。 (如果你不知道什么是浮点误差, 这段话可以理解为: 对于大多数的算法, 你可以正常地使用浮点数类型而不用对它进行特殊的处理)

【输入输出样例】

输入样例#1：

3 2 3 3
2 1 2
1 2 1
0.8 0.2 0.5
1 2 5
1 3 3
2 3 1

输出样例#1：

2.80

【样例1说明】

所有可行的申请方案和期望收益如下表:

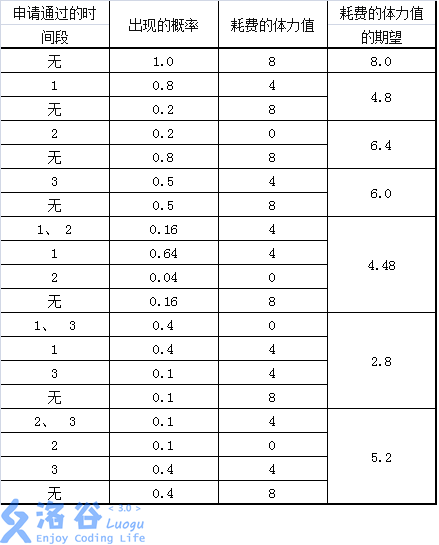
【提示】

1. 道路中可能会有多条双向道路连接相同的两间教室。 也有可能有道路两端连接

的是同一间教室。

2.请注意区分n,m,v,e的意义, n不是教室的数量, m不是道路的数量。

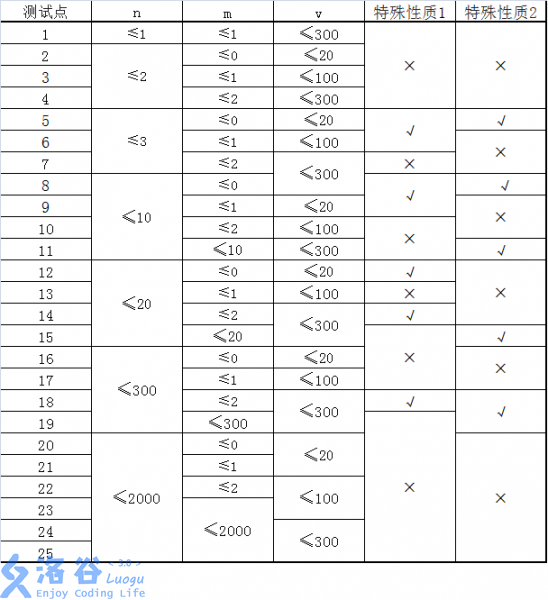
特殊性质1:图上任意两点 ai, bi, ai≠ bi间,存在一条耗费体力最少的路径只包含一条道路。

特殊性质2:对于所有的1≤ i≤ n， ki= 1 。

483 055 310

/*
    输入两个教室之间的距离的时候，可能一条边出现很多次，但是边权不一样。
*/
#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
int n,m,v,e,a[],b[];
double p[],ans=,ansnow,map[][];
bool q[];
void dfs2(int pos,int id,double P,double s){
    if(id==n){
        ansnow+=P*s;
        return;
    }
    if(!q[id+]){dfs2(a[id+],id+,P,s+map[pos][a[id+]]);}
    if(q[id+]){
        dfs2(a[id+],id+,P*(-p[id+]),s+map[pos][a[id+]]);
        dfs2(b[id+],id+,P*p[id+],s+map[pos][b[id+]]);
    }
}
void dfs1(int pos,int cnt){
    ansnow=;
    dfs2(,,,);
    ans=min(ans,ansnow);
    if(cnt==m+)return;
    for(int i=pos+;i<=n;i++){
        q[i]=;
        dfs1(i,cnt+);
        q[i]=;
    }
}
int main(){
    freopen("testdata(1).in","r",stdin);
    scanf("%d%d%d%d",&n,&m,&v,&e);
    for(int i=;i<=n;i++)scanf("%d",&a[i]);
    for(int i=;i<=n;i++)scanf("%d",&b[i]);
    for(int i=;i<=n;i++)scanf("%lf",&p[i]);
    memset(map,0x3f,sizeof(map));
    int x,y,z;
    for(int i=;i<=v;i++)
        for(int j=;j<=v;j++)map[i][j]=;
    for(int i=;i<=e;i++){
        scanf("%d%d%d",&x,&y,&z);
        if(z>map[x][y])continue;
        map[x][y]=map[y][x]=z;
    }
    for(int i=;i<=v;i++)map[i][i]=map[][i]=map[i][]=;
    for(int k=;k<=v;k++)
        for(int i=;i<=v;i++)
            for(int j=;j<=v;j++){
                if(i==j||i==k||j==k)continue;
                map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
            }
    dfs1(,);
    printf("%.2lf",ans);
}

80分 暴力by myl

#include<iostream>
#include<cstdio>
#include<cstring>
#define M 2010
#define N 310
using namespace std;
int n,m,v,e,a[M],b[M],dis[N][N];
int wantt[M],ok[M];
double qi[M],thiss,ans=100000000.0;
void floyed(){
    for(int k=;k<=v;k++)
        for(int i=;i<=v;i++)
            for(int j=;j<=v;j++)
                if(i!=j&&i!=k&&j!=k)
                    dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
double check2(double lv){
    int now=a[];int tot=;
    if(ok[]==)now=b[];
    for(int i=;i<=n;i++){
        if(ok[i]){
            if(now!=b[i])tot+=dis[now][b[i]];
            now=b[i];
        }
        else {
            if(now!=a[i])tot+=dis[now][a[i]];
            now=a[i];
        }
    }
    return lv*(double)tot;
}
void dfs2(int x,double lv){
    if(x==n+){
        thiss+=check2(lv);return;
    }
    if(!wantt[x]){
        dfs2(x+,lv);
    }
    else {
        dfs2(x+,lv*(1.0-qi[x]));
        ok[x]=;dfs2(x+,lv*qi[x]);ok[x]=;
    }
}
void check1(){
    thiss=;
    dfs2(,1.0);
    ans=min(ans,thiss);
}
void dfs1(int x,int t){
    if(t>m)return;
    if(x==n+){
        check1();return;
    }
    dfs1(x+,t);
    wantt[x]=;dfs1(x+,t+);wantt[x]=;
}
int main(){
    memset(dis,/,sizeof(dis));
    scanf("%d%d%d%d",&n,&m,&v,&e);
    for(int i=;i<=n;i++)
        scanf("%d",&a[i]);
    for(int i=;i<=n;i++)
        scanf("%d",&b[i]);
    for(int i=;i<=n;i++)
        scanf("%lf",&qi[i]);
    for(int i=;i<=e;i++){
        int x,y,z;scanf("%d%d%d",&x,&y,&z);
        if(x==y)continue;
        dis[x][y]=min(dis[x][y],z);
        dis[y][x]=min(dis[y][x],z);
    }
    floyed();
    if(m==){
        printf("%.2lf",check2(1.0));
    }
    else {
        dfs1(,);
        printf("%.2lf",ans);
    }
    fclose(stdin);fclose(stdout);
    return ;
}

80分 暴力

#include<iostream>
#include<cstdio>
using namespace std;
const int maxn=;
int n,m,V,E,c[maxn],d[maxn];
double t[maxn],map[maxn][maxn],dp[maxn][maxn][],ans;
int main() {
    scanf("%d%d%d%d",&n,&m,&V,&E);
    for(int i=;i<=n;++i) scanf("%d",&c[i]);
    for(int i=;i<=n;++i) scanf("%d",&d[i]);
    for(int i=;i<=n;++i) scanf("%lf",&t[i]);
    int x,y;
    double z;
    for(int i=;i<=V;i++)
        for(int j=;j<=V;j++)
            map[i][j]=0x7fffffff;
    for(int i=;i<=E;i++) {
        scanf("%d%d%lf",&x,&y,&z);
        map[x][y]=min(map[x][y],z);
        map[y][x]=map[x][y];
    }
    for(int i=;i<=V;i++)map[i][i]=;
    for(int k=;k<=V;k++)
        for(int i=;i<=V;i++)
            for(int j=;j<=V;j++)
                if(i!=j&&i!=k&&j!=k) {
                    map[i][j]=min(map[i][j],map[i][k]+map[k][j]);
                }
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++)
            dp[i][j][]=dp[i][j][]=0x7fffffff;
    ans=0x7fffffff;
    dp[][][]=dp[][][]=;
    for(int i=;i<=n;i++) {
        dp[i][][]=dp[i-][][]+map[c[i-]][c[i]];
        dp[i][][]=0x7fffffff;
        double w=map[c[i-]][c[i]];
        double x=(map[d[i-]][c[i]]-w)*t[i-]+w;
        double y=(map[c[i-]][d[i]]-w)*t[i]+w;
        double z=(-t[i-])*(-t[i])*map[c[i-]][c[i]]+(-t[i-])*t[i]*map[c[i-]][d[i]]+t[i-]*(-t[i])*map[d[i-]][c[i]]+t[i-]*t[i]*map[d[i-]][d[i]];
        for(int j=;j<=m&&j<=i;j++) {
            dp[i][j][]=min(dp[i-][j][]+w,dp[i-][j][]+x);
            dp[i][j][]=min(dp[i-][j-][]+y,dp[i-][j-][]+z);
        }
    }
    for(int i=; i<=m; i++) {
        ans=min(ans,dp[n][i][]);
        ans=min(ans,dp[n][i][]);
    }
    printf("%.2lf",ans);
}

100分 概率dp

P2827 蚯蚓

【题目描述】

本题中，我们将用符号\lfloor c \rfloor⌊c⌋表示对c向下取整，例如：\lfloor 3.0 \rfloor= \lfloor 3.1 \rfloor=\lfloor 3.9 \rfloor=3⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3。

蛐蛐国最近蚯蚓成灾了！隔壁跳蚤国的跳蚤也拿蚯蚓们没办法，蛐蛐国王只好去请神刀手来帮他们消灭蚯蚓。

蛐蛐国里现在共有n只蚯蚓（n为正整数)。每只蚯蚓拥有长度，我们设第i只蚯蚓的长度为a_i(i=1,2,...,n)a​i​​(i=1,2,...,n)，并保证所有的长度都是非负整数（即:可能存在长度为0的蚯蚓）。

每一秒，神刀手会在所有的蚯蚓中，准确地找到最长的那一只（如有多个则任选一个）将其切成两半。神刀手切开蚯蚓的位置由常数p(是满足0<p<1的有理数)决定，设这只蚯蚓长度为x，神刀手会将其切成两只长度分别为\lfloor px \rfloorlfloorpx⌋和x-\lfloor px \rfloorx−⌊px⌋的蚯蚓。特殊地，如果这两个数的其中一个等于0，则这个长度为0的蚯蚓也会被保留。此外，除了刚刚产生的两只新蚯蚓，其余蚯蚓的长度都会增加q(是一个非负整常数)。

蛐蛐国王知道这样不是长久之计，因为蚯蚓不仅会越来越多，还会越来越长。蛐蛐国王决定求助于一位有着洪荒之力的神秘人物，但是救兵还需要m秒才能到来......

(m为非负整数）

蛐蛐国王希望知道这m秒内的战况。具体来说，他希望知道：

•m秒内，每一秒被切断的蚯蚓被切断前的长度（有m个数）

•m秒后，所有蚯蚓的长度（有n+m个数)。

蛐蛐国王当然知道怎么做啦！但是他想考考你......

【输入输出格式】

输入格式：

第一行包含六个整数n,m,q,u,v,t，其中：n,m,q的意义见【问题描述】；u,v,t均为正整数；你需要自己计算p=u/v(保证0<u<v)t是输出参数，其含义将会在【输出格式】中解释。

第二行包含n个非负整数，为a_i,a_2,...,a_na​i​​,a​2​​,...,a​n​​，即初始时n只蚯蚓的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。

保证1 \le n \le 10^51≤n≤10​5​​，0<m \le 7*10^60<m≤7∗10​6​​，0 \le u<v \le 10^90≤u<v≤10​9​​，0 \le q \le 2000≤q≤200，1 \le t \le 711≤t≤71，0<ai \le 10^80<ai≤10​8​​。

输出格式：

第一行输出\lfloor m/t \rfloor⌊m/t⌋个整数，按时间顺序，依次输出第t秒，第2t秒，第3t秒……被切断蚯蚓（在被切断前）的长度。

第二行输出\lfloor (n+m)/t \rfloor⌊(n+m)/t⌋个整数，输出m秒后蚯蚓的长度；需要按从大到小的顺序，依次输出排名第t，第2t，第3t……的长度。

同一行中相邻的两个数之间，恰好用一个空格隔开。即使某一行没有任何数需要 输出，你也应输出一个空行。

请阅读样例来更好地理解这个格式。

【输入输出样例】

输入样例#1：

3 7 1 1 3 1
3 3 2

输出样例#1：

3 4 4 4 5 5 6
6 6 6 5 5 4 4 3 2 2

输入样例#2：

3 7 1 1 3 2
3 3 2

输出样例#2：

4 4 5
6 5 4 3 2

输入样例#3：

3 7 1 1 3 9
3 3 2

输出样例#3：

//空行
2

【样例解释1】

在神刀手到来前：3只蚯蚓的长度为3,3,2。

1秒后：一只长度为3的蚯蚓被切成了两只长度分别为1和2的蚯蚓，其余蚯蚓的长度增加了1。最终4只蚯蚓的长度分别为(1,2),4,3。括号表示这个位置刚刚有一只蚯蚓被切断

2秒后：一只长度为4的蚯蚓被切成了1和3。5只蚯蚓的长度分别为：2,3,(1,3),4。

3秒后：一只长度为4的蚯蚓被切断。6只蚯蚓的长度分别为：3,4,2,4,(1,3)。

4秒后：一只长度为4的蚯蚓被切断。7只蚯蚓的长度分别为：4,(1,3),3,5,2,4。

5秒后：一只长度为5的蚯蚓被切断。8只蚯蚓的长度分别为：5,2,4,4,(1,4),3,5。

6秒后：一只长度为5的蚯蚓被切断。9只蚯蚓的长度分别为：（1,4),3,5,5,2,5,4,6。

7秒后：一只长度为6的蚯蚓被切断。10只蚯蚓的长度分别为：2,5,4,6,6,3,6,5,(2,4)。所以，7秒内被切断的蚯蚓的长度依次为3,4,4,4,5,5,6。7秒后，所有蚯蚓长度从大到小排序为6,6,6,5,5,4,4,3,2,2

【样例解释2】

这个数据中只有t=2与上个数据不同。只需在每行都改为每两个数输出一个数即可。

虽然第一行最后有一个6没有被输出，但是第二行仍然要重新从第二个数再开始输出。

【样例解释3】

这个数据中只有t=9与上个数据不同。

注意第一行没有数要输出，但也要输出一个空行。

【数据范围】

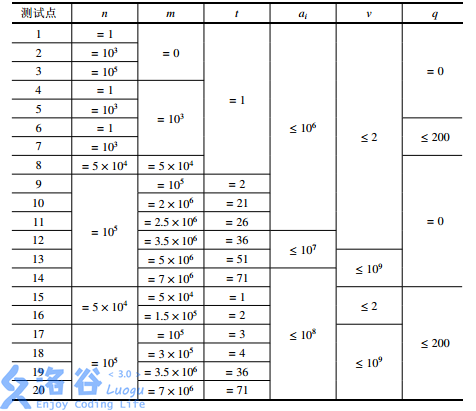
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int maxn=;
const int maxm=;
int n,m,q,u,v,t,ans1[maxm],a[maxn+maxm],len;
int cmp(int x,int y){
    return x>y;
}
void work1(){
    len=n;
    for(int i=;i<=m;i++){
        sort(a+,a+len+);
        ans1[i]=a[len];
        int x=a[len]*u/v,y=a[len];
        a[len]=x;
        a[++len]=y-x;
        for(int j=;j<=len-;j++)a[j]+=q;
    }
    int i=;
    while(){
        i++;
        if(i*t>m)break;
        printf("%d ",ans1[i*t]);
    }printf("\n");
    i=;
    sort(a+,a+m+n+,cmp);
    while(){
        i++;
        if(i*t>n+m)break;
        printf("%d ",a[i*t]);
    }
}
priority_queue<int>q1;
void work2(){
    for(int i=;i<=n;i++)q1.push(a[i]);
    for(int i=;i<=m;i++){
        int now=q1.top();q1.pop();
        int x=now*u/v;
        q1.push(x);
        q1.push(now-x);
        ans1[i]=now;
    }
    int i=;
    while(){
        i++;
        if(i*t>m)break;
        printf("%d ",ans1[i*t]);
    }printf("\n");
    for(int i=;i<=n+m;i++){
        a[i]=q1.top();q1.pop();
    }
    for(int i=;i<=(n+m)/t;i++)
        printf("%d ",a[i*t]);
}
int main(){
    freopen("earthworm.in","r",stdin);
    freopen("earthworm.out","w",stdout);
    scanf("%d%d%d%d%d%d",&n,&m,&q,&u,&v,&t);
    for(int i=;i<=n;i++)scanf("%d",&a[i]);
    if(q==)work2();
    else work1();
    return ;
}

55分 堆+暴力

洛谷2827 蚯蚓

P2831 愤怒的小鸟

【题目描述】

Kiana最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于(0,0)处，每次Kiana可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如y=ax^2+bxy=ax​2​​+bx的曲线，其中a,b是Kiana指定的参数，且必须满足a<0。

当小鸟落回地面(即x轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有n只绿色的小猪，其中第i只小猪所在的坐标为(xi,yi)。

如果某只小鸟的飞行轨迹经过了(xi,yi),那么第i只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过(xi,yi)，那么这只小鸟飞行的全过程就不会对第i只小猪产生任何影响。

例如，若两只小猪分别位于(1,3)和(3,3)，Kiana可以选择发射一只飞行轨迹为y=-x^2+4xy=−x​2​​+4x的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有T个关卡，现在Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

【输入输出格式】

输入格式：

第一行包含一个正整数T，表示游戏的关卡总数。

下面依次输入这T个关卡的信息。每个关卡第一行包含两个非负整数n,m，分别表示该关卡中的小猪数量和Kiana输入的神秘指令类型。接下来的n行中，第i行包含两个正实数(xi,yi)，表示第i只小猪坐标为(xi,yi)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果m=0，表示Kiana输入了一个没有任何作用的指令。

如果m=1，则这个关卡将会满足：至多用\left \lceil \frac{n}{3} + 1 \right \rceil⌈​3​​n​​+1⌉只小鸟即可消灭所有小猪。

如果m=2,则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少\left \lfloor \frac{n}{3} \right \rfloor⌊​3​​n​​⌋只小猪。

保证1<=n<=18，0<=m<=2，0<xi,yi<10，输入中的实数均保留到小数点后两位。

上文中，符号\left \lceil x \right \rceil⌈x⌉和\left \lfloor x \right \rfloor⌊x⌋分别表示对c向上取整和向下取整

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量

【输入输出样例】

输入样例#1：

2
2 0
1.00 3.00
3.00 3.00
5 2
1.00 5.00
2.00 8.00
3.00 9.00
4.00 8.00
5.00 5.00

输出样例#1：

1
1

输入样例#2：

3
2 0
1.41 2.00
1.73 3.00
3 0
1.11 1.41
2.34 1.79
2.98 1.49
5 0
2.72 2.72
2.72 3.14
3.14 2.72
3.14 3.14
5.00 5.00

输出样例#2：

2
2
3

输入样例#3：

1
10 0
7.16 6.28
2.02 0.38
8.33 7.78
7.68 2.09
7.46 7.86
5.77 7.44
8.24 6.72
4.42 5.11
5.42 7.79
8.15 4.99

输出样例#3：

6

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同，2只小猪分别位于（1.00,3.00)和 (3.00,3.00)，只需发射一只飞行轨迹为y = -x^2 + 4x的小鸟即可消灭它们。

第二个关卡中有5只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

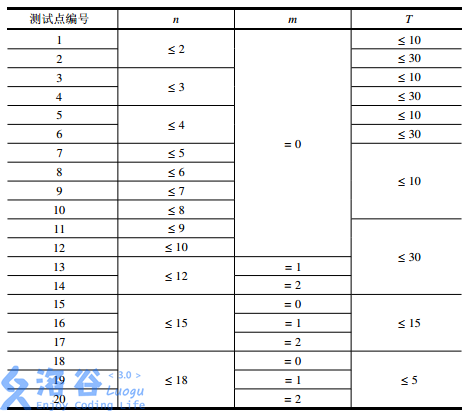
#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<cmath>
#define N 20
using namespace std;
int n,m,limit,ok[N],ans,q[N];
double x[N],y[N],a,b;
void check(int i,int j){
    double x1=x[i],x2=x[j],y1=y[i],y2=y[j];
    double P=x1/x2;
    a=(y2*P-y1)/(x2*x1-x1*x1);
    b=(y1-a*x1*x1)/x1;
}
void dfs(int t){
    if(t>limit)return;
    if(t>=ans)return;
    int flag=;
    for(int i=;i<=n;i++){
        if(ok[i])continue;
        ok[i]=;flag=;int fl2=;
        for(int j=i+;j<=n;j++){
            if(ok[j])continue;
            check(i,j);
            if(a>=)continue;
            ok[j]=;fl2=;
            int num=;
            for(int k=j+;k<=n;k++){
                double yy=a*x[k]*x[k]+b*x[k]-y[k];
                if(abs(yy)<=0.001){
                    ok[k]=;q[++num]=k;
                }
            }
            dfs(t+),ok[i]=ok[j]=;
            for(int i=;i<=num;i++)ok[q[i]]=;
        }
        if(!fl2)dfs(t+),ok[i]=;
    }
    if(!flag){
        ans=min(ans,t);
        return;
    }
}
void work(){
    scanf("%d%d",&n,&m);
    if(m==)limit=n;
    else if(m==)limit=min(n/+,n);
    else limit=min(n,n-n/+);
    for(int i=;i<=n;i++)
        scanf("%lf%lf",&x[i],&y[i]);
    dfs();
    printf("%d\n",ans);
}
int main(){
    freopen("angrybirds.in","r",stdin);
    freopen("angrybirds.out","w",stdout);
    int T;scanf("%d",&T);
    while(T--){
        memset(ok,,sizeof(ok));
        ans=N;
        work();
    }
    fclose(stdin);fclose(stdout);
    return ;
}

50分 暴力

洛谷P2831 愤怒的小鸟