算法复习——树形dp

树形dp的状态转移分为两种,一种为从子节点到父节点，一种为父节点到子节点，下面主要讨论子节点到父亲节点的情况：

例题1(战略游戏)：

这是一道典型的由子节点状态转移到父节点的问题，而且兄弟节点之间没有相互影响，我们用f[i][0]/f[i][1]表示i不取/要取时其所在子树总共最少取的节点数,不难得出dp方程：

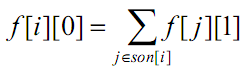
代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<cstring>
#include<string>
#include<algorithm>
#include<cstdio>
#include<cstdlib>
#include<vector>
using namespace std;
const int N=;
int first[N],next[N*],go[N*],tot,n,father[N],f[N][];
vector<int>son[N];
inline int R()
{
  char c;int f=;
  for(c=getchar();c<''||c>'';c=getchar());
  for(;c<=''&&c>='';c=getchar())
    f=(f<<)+(f<<)+c-'';
  return f;
}
inline void comb(int a,int b)
{
  next[++tot]=first[a],first[a]=tot,go[tot]=b;
  next[++tot]=first[b],first[b]=tot,go[tot]=a;
}
inline void dfs(int u,int fa)
{
  for(int e=first[u];e;e=next[e])
  {
    int v=go[e];
    if(v==fa)  continue;
    father[v]=u;
    son[u].push_back(v);
    dfs(v,u);
  }
}
inline void dp(int u)
{
  int temp=1e+;
  if(!son[u].size())
  {
    f[u][]=;f[u][]=;
    return;
  }
  for(int i=;i<son[u].size();i++)
  {
    dp(son[u][i]);
    f[u][]+=f[son[u][i]][];
    f[u][]+=min(f[son[u][i]][],f[son[u][i]][]);
  }
  f[u][]++;
}
int main()
{
  //freopen("a.in","r",stdin);
  int a,b,c;
  n=R();
  for(int i=;i<=n;i++)
  {
    a=R(),b=R();
    for(int j=;j<=b;j++)
      c=R(),comb(a,c);
  }
  dfs(,);dp();
  int ans=min(f[][],f[][]);
  cout<<ans<<endl;
  return ;
}

通过这道题我们也可以看出,如果兄弟节点间并不存在相互影响制约的关系，dp的第二维通常是非常小的

那么当兄弟节点间会相互影响时，又该怎么办,我们先讨论较为简单的二叉树的情况：

例题2(二叉苹果树)：

首先将保留树枝数量转化成保留节点数量+1,（不转化也可以），然后每个树枝上的苹果数量设为相应节点的点权，我们发现，如果用f[i][k]表示i所在子树总共留下了k个节点，由于儿子节点只有两个，我们就可以枚举左儿子保留的节点数量x，则右儿子即为k-x-1，推出dp方程：

f[i][k]=max{f[lson][x]+f[rson][k-x-1],f[i][k]},0<=x<k

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=;
int first[N],next[N*],go[N*],val[N*],tot;
int n,m;
int dp[N][N];
inline void comb(int a,int b,int c)
{
  next[++tot]=first[a],first[a]=tot,go[tot]=b,val[tot]=c;
  next[++tot]=first[b],first[b]=tot,go[tot]=a,val[tot]=c;
}
inline void dfs(int u,int fa,int Val,int k)
{
  if(u==||k==)
  {
    dp[u][k]=;
    return;
  }
  if(dp[u][k]!=-)
    return;
  dp[u][k]=;
  for(int i=;i<k;i++)
  {
    int l=,r=,vl,vr;
    for(int e=first[u];e;e=next[e])
    {
      int v=go[e];
      if(v==fa)  continue;
      if(l==)
        l=v,vl=val[e];
      else
      {
        r=v,vr=val[e];
        break;
      }
    }
    dfs(l,u,vl,i);
    dfs(r,u,vr,k-i-);
    dp[u][k]=max(dp[l][i]+dp[r][k-i-]+Val,dp[u][k]);
  }
  return;
}
int main()
{
  //freopen("a.in","r",stdin);
  scanf("%d%d",&n,&m);
  m++;
  memset(dp,-,sizeof(dp));
  int a,b,c;
  for(int i=;i<n;i++)
  {
    scanf("%d%d%d",&a,&b,&c);
    comb(a,b,c);
  }
  dfs(,,,m);
  cout<<dp[][m]<<endl;
  return ;
}

通过这道题，我们可以发现，如果兄弟节点间存在着相互影响的情况，那么常常会在dfs之前枚举儿子状态，保证儿子的状态不冲突，由于枚举会出现重复的情况，我们也常常会用到记忆化搜索

上面只是两个儿子的情况，如果面对多个儿子，上面的方法显然是不可取的

例题3(选课)：

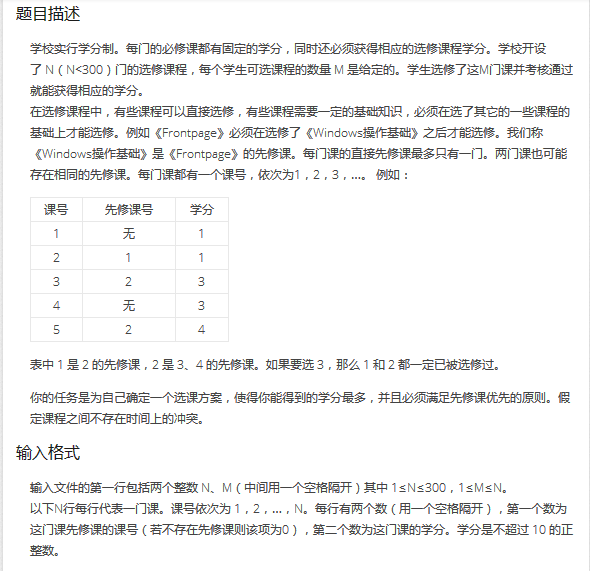
根据题意由先修课向它的课程连边，建成一颗树，树的点权对应课程学分

此时我们必须将多叉树转化为二叉树：把第一个孩子作为父节点的左子树，其它孩子作为第一个孩子的右子树。

具体实现为：每次读入一个节点i的儿子j，我们将son[i]=j，而将brother[j]设为之前的son[i]，也就是离j最近的兄弟节点。

设f[u][k]为新建的二叉树的后，节点u所在子树保留k个儿子能得到得最多学分，可以得出dp方程：

f[u][k]=max(f[u][k],f[son[u]][i]+dp[brother[u]][k-i-1]+val[u]),0<=i<k;

其中val表示该节点对应课程的的学分

由实际意义不难发现，我们这样枚举少考虑了一个情况，也就是当前u节点所对应的原来的图的子树的节点都不取的情况，

因此在最后我们还要这样：

f[u][k]=max(f[u][k],f[brother[u]][k])

多叉树转二叉树的方法是面对分配附加维时常用的一种方法

例题4（偷天换日，洛谷3360）：

首先要考虑的是这道题的建图，如果根据题意新建一个图是在太麻烦，因此我们可以直接考虑边读入信息边再已知的树上dfs，（详细见代码）

用f[i][j]表示已i为节点的子树（包含i与其父亲连接的边）中花费j的时间能获得的最大价值

当我们dfs到展览室的时候，f[i][j]的计算无疑是一个01背包问题，在此不多叙述

其他情况我们可以发现，除去末端展览室的情况，树的其他部分都是一颗二叉树，因此直接用我们上面提到的方法即可：

f[x][i]=max(f[x][i],f[l][j]+f[r][i-j-dis]);dis<=i<=n,j<=i-dis;

其中dis表示i与其父节点连接的边的权值；

代码如下：（引用洛谷题解）

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define ll long long
ll n,m=;
ll f[][]={};
ll value[],tim[];
inline void sca(ll x)
{
    ll dis,pd;
    scanf("%lld%lld",&dis,&pd);
    dis*=;
    if(pd)
    {
        for(ll j=;j<=pd;j++)
        scanf("%lld%lld",&value[j],&tim[j]);
        for(ll i=;i<=pd;i++)
            for(ll j=n;j>=tim[i];j--)
            if(j-tim[i]>=dis)
            f[x][j]=max(f[x][j],f[x][j-tim[i]]+value[i]);
        return;
    }
    ll l=++m;sca(m);
    ll r=++m;sca(m);
    for(ll i=dis;i<=n;i++)
    for(ll j=;j<=i-dis;j++)f[x][i]=max(f[x][i],f[l][j]+f[r][i-j-dis]);
}
int main()
{
    scanf("%lld",&n);n--;
    sca();
    printf("%lld",f[][n]);
    return ;
}

例题5(骑士，bzoj1040)：

首先想到的是如果按照痛恨关系建边的话有两种情况：有一个环或者为一颗树，为树的话就和例题1一样了，十分简单，因此主要考虑有环的情况.

为了让环更好处理，我们选择从被痛恨者向痛恨他的人连一条边····这样整个图即为奇环外向树（只有一个环且没有环外的点指向环内的点的图）

这样的话我们可以找环上任意一点u让它与它的父节点father[u]断开，然后以它为根进行dp，dp方程与例题1一样。

然而这样会出现冲突，因为最优答案有可能是由f[father[u]][1]更新过来的，因此我们要将环上的的点单独处理

首先直接将f[father[u]][1]赋值为f[father[u]][0]这样的话可以保证u取了而father[u]一定没有取,然后依次往father[father[u]],father[father[father[u]]]·····跳，即重新遍历整个环,依次更新遍历的点的f[][0],f[][1],直到跳到u为止

最后只更新f[u][1]就好了,ans加上max{f[u][1],f[u][0]}.

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=1e6+;
int first[N],next[N],go[N],tot,n,val[N],father[N],g[N];
long long ans=,f[N][];
bool visit[N];
inline int R()
{
  char c;int f=;
  for(c=getchar();c<''||c>'';c=getchar());
  for(;c<=''&&c>='';c=getchar())
    f=(f<<)+(f<<)+c-'';
  return f;
}
inline void comb(int a,int b)
{
  next[++tot]=first[a],first[a]=tot,go[tot]=b;
}
inline void dfs(int u)
{
  visit[u]=true;f[u][]=val[u];
  for(int e=first[u];e;e=next[e])
  {
    int v=go[e];
    if(!visit[v])
    {
      dfs(v);
      f[u][]+=max(f[v][],f[v][]);
      f[u][]+=f[v][];
    }
  }
}
inline void dp(int a)
{
  int root;
  for(root=a;g[root]!=a;root=father[root])
    g[root]=a;
  dfs(root);
  int b=father[root];
  f[b][]=f[b][];
  for(int x=father[b];x!=root;x=father[x])
  {
    f[x][]=val[x],f[x][]=;
    for(int e=first[x];e;e=next[e])
    {
      int v=go[e];
      f[x][]+=max(f[v][],f[v][]);
      f[x][]+=f[v][];
    }
  }
  f[root][]=val[root];
  for(int e=first[root];e;e=next[e])
  {
    int v=go[e];
    f[root][]+=f[v][];
  }
  ans+=max(f[root][],f[root][]);
}
int main()
{
  //freopen("a.in","r",stdin);
  n=R();int a,b;
  for(int i=;i<=n;i++)
  {
    a=R(),b=R();
    val[i]=a,comb(b,i);
    father[i]=b;
  }
  for(int i=;i<=n;i++)
    if(!visit[i])
      dp(i);
  printf("%lld",ans);
  return ;
}

例题6（bzoj1023仙人掌）

Description

　　如果某个无向连通图的任意一条边至多只出现在一条简单回路（simple cycle）里，我们就称这张图为仙人掌
图（cactus）。所谓简单回路就是指在图上不重复经过任何一个顶点的回路。

　　举例来说，上面的第一个例子是一张仙人图，而第二个不是——注意到它有三条简单回路：（4，3，2，1，6
，5，4）、（7，8，9，10，2，3，7）以及（4，3，7，8，9，10，2，1，6，5，4），而（2，3）同时出现在前两
个的简单回路里。另外，第三张图也不是仙人图，因为它并不是连通图。显然，仙人图上的每条边，或者是这张仙
人图的桥（bridge），或者在且仅在一个简单回路里，两者必居其一。定义在图上两点之间的距离为这两点之间最
短路径的距离。定义一个图的直径为这张图相距最远的两个点的距离。现在我们假定仙人图的每条边的权值都是1
，你的任务是求出给定的仙人图的直径。

Input

　　输入的第一行包括两个整数n和m（1≤n≤50000以及0≤m≤10000）。其中n代表顶点个数，我们约定图中的顶
点将从1到n编号。接下来一共有m行。代表m条路径。每行的开始有一个整数k（2≤k≤1000），代表在这条路径上
的顶点个数。接下来是k个1到n之间的整数，分别对应了一个顶点，相邻的顶点表示存在一条连接这两个顶点的边
。一条路径上可能通过一个顶点好几次，比如对于第一个样例，第一条路径从3经过8，又从8返回到了3，但是我们
保证所有的边都会出现在某条路径上，而且不会重复出现在两条路径上，或者在一条路径上出现两次。

Output

　　只需输出一个数，这个数表示仙人图的直径长度。

Sample Input

15 3
9 1 2 3 4 5 6 7 8 3
7 2 9 10 11 12 13 10
5 2 14 9 15 10 8
10 1
10 1 2 3 4 5 6 7 8 9 10

Sample Output

8
9

HINT

对第一个样例的说明：如图，6号点和12号点的最短路径长度为8，所以这张图的直径为8。

【注意】使用Pascal语言的选手请注意：你的程序在处理大数据的时候可能会出现栈溢出。

如果需要调整栈空间的大小，可以在程序的开头填加一句：{$M 5000000}，其中5000000即

指代栈空间的大小，请根据自己的程序选择适当的数值。

这道题不得不说是真tm难啊····

题解详见：http://z55250825.blog.163.com/blog/static/150230809201412793151890/

说说我理解的吧····先进行一遍dfs造一颗树用f[i]表示从i往深处的链能到达的最大距离，注意是链，不是环·····,那么用这个尝试更新答案,(用u的儿子的f的次大值和最大值的和+1来更新)

然后我们要讨论的就是如何处理环上的情况····

对于环的话我们找到环上深度最高的点u，我们要按照f的定义求出f[u]，（这里有点难想，设i为环上除u外的点，那么我们可以推出f[u]=max{f[i]+dis(u,i)},于是以后dfs到环上的话答案一定由f[u]更新而来

接下来我们就要解决如何算f[u],并且在更新答案时我们还忽略了环上的点可以更新答案,打个比方，如果环上有两个点i,j,那么答案可能由f[i]+f[j]+dis(i,j)更新而来·····

我们要先提取出这个环,然后利用单调队列来求这个东西····具体实现看代码吧,···大概有点类似于烽火传递····队列首与队列尾的距离不能大于环长度的一半（不然就不是最短距离）,然后还要保持一个单调性···

代码：

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<ctime>
#include<cctype>
#include<cstring>
#include<string>
#include<algorithm>
using namespace std;
const int N=5e4+;
int n,m,k,f[N],low[N],dfn[N],cnt,deep[N],father[N],tol;
int first[N],go[N*],next[N*],tot,ans=,queue[N*],a[N*];
inline int R()
{
  char c;int f=;
  for(c=getchar();c<''||c>'';c=getchar());
  for(;c<=''&&c>='';c=getchar())
    f=(f<<)+(f<<)+c-'';
  return f;
}
void comb(int a,int b)
{
  next[++tot]=first[a],first[a]=tot,go[tot]=b;
  next[++tot]=first[b],first[b]=tot,go[tot]=a;
}
void init()
{
  n=R(),m=R();int a,b;
  while(m--)
  {
    k=R();a=R();
    for(int i=;i<k;i++)  b=R(),comb(a,b),a=b;
  }
}
void dp(int root,int u)
{
  int tail=,head=;tol=deep[u]-deep[root]+;
  for(int i=u;i!=root;i=father[i])
    a[tol--]=f[i];
  a[tol]=f[root],tol=deep[u]-deep[root]+;
  for(int i=tol+;i<=tol*;i++)
    a[i]=a[i-tol];
  queue[head]=;
  for(int i=;i<=tol+tol/;i++)
  {
    while(head<=tail&&queue[head]<i-tol/)  head++;
    ans=max(ans,a[queue[head]]+a[i]+i-queue[head]);
    while(head<=tail&&a[queue[tail]]-queue[tail]<=a[i]-i)  tail--;
    queue[++tail]=i;
  }
  for(int i=;i<=tol;i++)
    f[root]=max(f[root],a[i]+min(i-,tol-i+));
}
void tarjan(int u)
{
  low[u]=dfn[u]=++cnt;
  for(int e=first[u];e;e=next[e])
  {
    int v=go[e];
    if(father[u]==v)  continue;
    if(!dfn[v])  father[v]=u,deep[v]=deep[u]+,tarjan(v);
    low[u]=min(low[v],low[u]);
    if(dfn[u]<low[v])  ans=max(ans,f[u]+f[v]+),f[u]=max(f[u],f[v]+);
  }
  for(int e=first[u];e;e=next[e])
  {
    int v=go[e];
    if(father[v]!=u&&dfn[u]<dfn[v])
      dp(u,v);
  }
}
int main()
{
  //freopen("a.in","r",stdin);
  init();
  tarjan();
  printf("%d\n",ans);
  return ;
}