【bzoj1002】[FJOI2007]轮状病毒 矩阵树定理+高精度

题目描述

轮状病毒有很多变种，所有轮状病毒的变种都是从一个轮状基产生的。一个N轮状基由圆环上N个不同的基原子和圆心处一个核原子构成的，2个原子之间的边表示这2个原子之间的信息通道。如下图所示

N轮状病毒的产生规律是在一个N轮状基中删去若干条边，使得各原子之间有唯一的信息通道，例如共有16个不同的3轮状病毒，如下图所示

现给定n(N<=100)，编程计算有多少个不同的n轮状病毒

输入

第一行有1个正整数n

输出

计算出的不同的n轮状病毒数输出

样例输入

3

样例输出

16

---

题解

矩阵树定理+高精度

求无向图生成树个数，显然使用矩阵树定理。

然后得到的行列式如下：

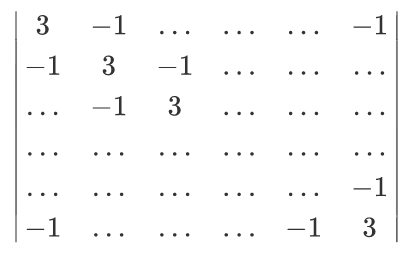
（-1和3处是相同的结构，其余位置为0）

然后可以使用高精度小数进行高斯消元，不过这样显然不够优雅。

手推一下这个行列式的性质，可以发现：$F(n)=3*F(n-1)-F(n-2)+2$。

这样就可以直接递推了。

高精度什么的使用Python就好啦。

n = int(input())
f = [0] * 105
f[1] = 1
for i in range(2 , n + 1):
	f[i] = 3 * f[i - 1] - f[i - 2] + 2
print(f[n])