Codevs 4357 不等数列

不等数列

【题目描述】

将1到n任意排列，然后在排列的每两个数之间根据他们的大小关系插入“>”和“<”。问在所有排列中，有多少个排列恰好有k个“<”。答案对2012取模。

【输入格式】

第一行2个整数n,k。

【输出格式】

一个整数表示答案。

【样例输入】

5 2

【样例输出】

66

【数据范围】

对于30%的数据：n <= 10

对于100%的数据：k < n <= 1000，

对于30% n<=10的数据，搜索打表，状态压缩动态规划......

对于1--n等类似的排列计数问题，以动态规划和组合数学2种大方向为基本解决方向。

组合数学在noip最难也就到杨辉三角左右，所以这题我从动态规划展开。

如果此类排列问题在脑中的模型是：“有n个格子，填入1--n”，那么相对应的DP就不得不记录哪些数填过了（从左到右填入）或者哪些格子填过了（从小到大填入）。这样一来就必须要使用状态压缩来存储这些信息，就使得复杂度变得难以接受。

而如果换个模型：“从小到大把数字插入数列”。注意是数列而不是格子，这样一来就不需要记录是哪些数字插入了（而只要记录插入到了第几个数字），同时不需要记录每个数字的具体位置，也不需要记录数字的相对位置，而只需记录相对关系的数目（对本题而言就是有几个“<”）。

因为是从小到大插入数字，所以当前插入的数字一定大于所有已经插入的。

蓝色是当前插入的数字，如果它插入到<关系的2个数字之间（或者数列最左端），就会使数列的<数量不变，>数量+1：

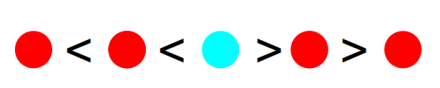
类似的，插入到>关系的2个数字之间（或者数列最右端），数列的<数量+1，>数量不变。

F[i][j]表示前i个数字构成的数列中，恰有j个‘<’号的方案数（‘>’号就有i-j-1个）。

F[i][j]=F[i-1][j-1]*(i-j)+F[i-1][j]*(j+1).

时空复杂度:O(n^2)

若打表则时间复杂度为O(1)

#include<iostream>
#include<cstdio>
using namespace std;
int n,k,f[][];
int main(){
    scanf("%d%d",&n,&k);
    for(int i=;i<=n;i++)f[i][]=;
    for(int i=;i<=n;i++)
        for(int j=;j<i;j++)
            f[i][j]=max(f[i][j],f[i-][j-]*(i-j)%+f[i-][j]*(j+)%)%;
    cout<<f[n][k];
}