第6章 图的学习总结（邻接矩阵&邻接表）

我觉得图这一章的学习内容更有难度，其实图可以说是树结构更为普通的表现形式，它的每个元素都可以与多个元素之间相关联，所以结构比树更复杂，然而越复杂的数据结构在现实中用途就越大了，功能与用途密切联系，所以，图结构非常重要，学习起来也是有点难度的，在于图的存储结构和逻辑结构，以及它与其他辅助数据结构相结合（链表，队列等），这需要很清晰的逻辑思维，才能把知识贯通。

这么重要的图，它的特别重要应用（最小生成树、最短路径、拓扑排序、关键路径），还有这些应用中一些著名算法，图的这章内容的丰富，让我大开眼界！

学习图最基础的内容，也是实现其他操作最基础、最关键的部分，就是图的存储结构，图的遍历。这里我准备总结一下在做题目时候对邻接矩阵、邻接表，深度优先搜索遍历、广度优先搜索遍历的理解，而对于应用的各种算法，还需要继续学习，才有更深刻的理解。

PTA上题目：列出连通集

给定一个有N个顶点和E条边的无向图，请用DFS和BFS分别列出其所有的连通集。假设顶点从0到N−1编号。进行搜索时，假设我们总是从编号最小的顶点出发，按编号递增的顺序访问邻接点。

输入格式:

输入第1行给出2个整数N(0<N≤10)和E，分别是图的顶点数和边数。随后E行，每行给出一条边的两个端点。每行中的数字之间用1空格分隔。

输出格式:

按照 “ { v1, v2, v3, ... ,vk } ”的格式，每行输出一个连通集。先输出DFS的结果，再输出BFS的结果。

输入样例:                         输出样例:

8 6　　　　　　　　　　　　{ 0 1 4 2 7 }
0 7　　　　　　　　　　　　{ 3 5 }
0 1　　　　　　　　　　　　{ 6 }
2 0　　　　　　　　　　　　{ 0 1 2 7 4 }
4 1　　　　　　　　　　　　{ 3 5 }
2 4　　　　　　　　　　　　{ 6 }
3 5 

跟据这道题题意，可明显以看出用邻接矩阵的存储结构较容易，而且输入中没有顶点名，直接用数组下标就可以，所以存储输入数据还是比较简单实现的，下面是邻接矩阵存储定义：

typedef int ArcType; //边
type char VerTexType;//顶点名字，这道题不需要用到
typedef struct
{
    VerTexType vexs[];//顶点表
        ArcType arcs[][];//邻接矩阵
    int vexnum,arcnum;//顶点数和边数
}AMGraph; 

接下来创建无向图：

void create(AMGraph &G)//邻接矩阵建立无向图
{
    int i,j,k;
    int x,y;
    cin>>G.vexnum>>G.arcnum;
    for(i=;i<G.vexnum;i++)//初始化矩阵元素值为0
    {
        for(j=;j<G.arcnum;j++)
        G.arcs[i][j]=;
    }
    for(k=;k<G.arcnum;k++)//输入一条边的两个端点
    {
        cin>>x>>y;
        G.arcs[x][y]=;//并将对应矩阵中元素值置1,表示此两点间存在边
        G.arcs[y][x]=;//无向图的矩阵为对称的
    }
}

因为题目的特殊性，找顶点对应的下标的LocateVex函数就省去了，直接用输入数据，所以简单很多。继续是图的遍历，先DFS算法，对于非连通图，需要两个函数来完成图的遍历，刚好这道题目也是输入连通分量，DFSAM函数是对一个连通分量的遍历，DFS是对整个图，有几个连通分量就调用几次DFSAM：

void DFSAM(AMGraph G,int v)//一个连通分量的深度优先搜索遍历
{
    int w;
    cout<<v<<" ";visit[v]=true;//输出第一个点，同时记录已经访问过
    for(w=;w<G.vexnum;w++)
    {
        if(G.arcs[v][w]!=&&(!visit[w]))     DFSAM(G,w);//对尚未访问过且与上一个顶点间存在边的顶点递归调用
    }
}

void DFS(AMGraph G)//非连通图的深度优先搜索遍历
{
    int v;
    for(v=;v<G.vexnum;v++)
        visit[v]=false;//标记数组初始化
    for(v=;v<G.vexnum;v++)
    {
        if(!visit[v])//对于未访问的顶点调用DFSAMG函数
        {    cout<<"{ ";
            DFSAM(G,v);
            cout<<"}"<<'\n';
        }
     }
}

继续是广度优先搜索遍历（BFS），感觉相对于DFS在算法上更难一点，需要借助队列的存储结构来完成，这跟上一章树的层次遍历差不多。上课时候讨论过有两种方法可以实现，一是先将顶点入队，再访问；二是先访问顶点，再入队，后者更优，它避免了将已经访问过的顶点进行多余的入队操作。

void BFSAM(AMGraph G,int v)//一个连通分量的广度优先搜索遍历
{
    queue<int> q;
    int w,x;
    cout<<v<<" ";//采用先访问再入队方法
    q.push(v);
    visit[v]=true;//入队第一个点，同时记录已经访问过
    while(!q.empty())//循环下面操作，直到队空
    {
        x=q.front();//记录此时队头顶点，再出队
        q.pop();
        for(w=;w<G.vexnum;w++)//遍历查找邻接点
        {
            if(G.arcs[x][w]!=&&(!visit[w]))//若两点间有边且未访问
            {
                cout<<w<<" "; //输入此顶点
                visit[w]=true;//标记已经访问过
                q.push(w);//将此点入队
            }
         }
    }
}

void BFS(AMGraph G)//非连通图的深广度优先搜索遍历
{
    int v;
    for(v=;v<G.vexnum;v++)
        visit[v]=false;
    for(v=;v<G.vexnum;v++)
    {
        if(!visit[v])//对于未访问的顶点调用DFSALG函数
        {    cout<<"{ ";
            BFSAM(G,v);
            cout<<"}"<<'\n';
        }
     }
}

对于上面邻接矩阵查找顶点的下一个邻接点和判断是否有边存在，是通过遍历所有顶点和一个if语句完成，而在邻接表中，这一步操作就不一样了。

邻接矩阵比较熟悉，容易操作，但它适合用在稠密图，空间复杂度高O（n²），稀疏图中尤其浪费空间，所以有时需要采用邻接表。因此，这道题我准备试一下用邻接表，顺便加深一下对算法的理解。邻接表存储结构的定义复杂许多，如下：

typedef struct Arcnode
{
    int ad;//顶点所在位置（下标）
    struct Arcnode *next;//指向下一条边的指针
}Arcnode;

typedef struct Vnode//顶点信息（表）
{
    Arcnode *first;
}Vnode,Al[];

typedef struct//邻接表
{
    Al ver;//顶点数组
    int vexnum,arcnum;//顶点数和边数
}ALGraph;

表头结点和边结点：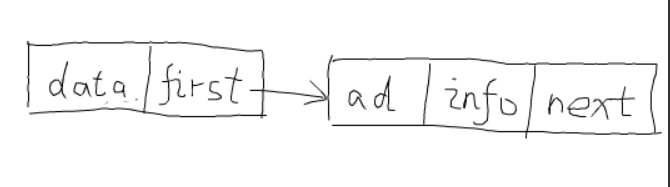

然后创建无向图就是对每个指针指向的操作：

void create(ALGraph &G)
{
    int i,j,k,x,y;
    Arcnode *p,*p1;
    cin>>G.vexnum>>G.arcnum;
    for(i=;i<G.vexnum;i++)
    G.ver[i].first=NULL;
    for(k=;k<G.arcnum;k++)//输入一条边的两个端点
    {
        cin>>x>>y;
        p=new Arcnode;//无向图的两点互相指向对方
        p->ad=y;p->next=G.ver[x].first;G.ver[x].first=p;
        p1=new Arcnode;
        p1->ad=x;p1->next=G.ver[y].first;G.ver[y].first=p1;
    }
}

开始我在新结点那里出错，出现很奇怪的结果，链式结构的存储确实很容易出现小错误，接着在DFSAL中跟矩阵判断条件有所不同，需要一个指针指向起始位置，在while循环里还有修改指针指向：

void DFSAL(ALGraph G,int v)//一个连通分量的深度优先搜索遍历
{
    int w;
    cout<<v<<" ";visit[v]=true;
    Arcnode *p2;
    p2=new Arcnode;
    //输出第一个点，同时记录已经访问过
    p2=G.ver[v].first;
    while(p2)
    {
        w=p2->ad;
        if(!visit[w])     DFSAL(G,w);//对尚未访问过且与上一个顶点间存在边的顶点递归调用
        p2=p2->next;
    }
}

邻接表的BFS算法操作有点难，我在这里卡了，出现许多错误，这里有队列，有链表，在判断和指针操作有些问题，开始问题出现有：没有定义指针变量指向访问顶点；在while循环之后未修改指针指向，导致死循环；再修改错误过程中，忘记将元素出队还有出队位置不对，运行出错。经过一波修改，最后终于成功了

void BFSAL(ALGraph G,int v)//一个连通分量的广度优先搜索遍历
{
    queue<int> q;
    int w,x;
    cout<<v<<" ";//采用先访问再入队方法
    q.push(v);
    visit[v]=true;//入队第一个点，同时记录已经访问过
    while(!q.empty())//循环下面操作，直到队空
    {
        x=q.front();//记录此时队头顶点，再出队
        Arcnode *p3;
        p3=new Arcnode;
        p3=G.ver[x].first;
        q.pop();
        while(p3)
        {
            w=p3->ad;
            if(!visit[w])//若两点间有边且未访问
            {
                cout<<w<<" "; //输入此顶点
                visit[w]=true;//标记已经访问过
                q.push(w);//将此点入队
            }
            p3=p3->next;
        }
    }
}

然后又发现一个问题，整个程序运行没有问题，但是与题目输出结果在第一个连通分量顺序不同，那究竟在哪有错误，我仔细看了一遍，画一下创建邻接表时候每个点的关系，最后发现是因为存储结构不同，就链表来说，这个创建的时候是前插法，输出顺序与输入顺序有关系，这道题要求“从编号最小的顶点出发，按编号递增的顺序访问邻接点”，就仅限于用邻接矩阵方法实现。

但在这个过程中发现问题，解决问题，更明白许多，特别对不太熟悉的邻接表方法，有更深的理解。下面是完整代码，虽然暂时不适应解决这道题，但以后可能要用到这种思想。

#include<iostream>
#include<queue>
using namespace std;
bool visit[];//访问标记数组
typedef int ArcType; //边 

typedef struct Arcnode
{
    int ad;
    struct Arcnode *next;
}Arcnode;

typedef struct Vnode
{
    Arcnode *first;
}Vnode,Al[];

typedef struct
{
    Al ver;
    int vexnum,arcnum;
}ALGraph;

void create(ALGraph &G)
{
    int i,j,k,x,y;
    Arcnode *p,*p1;
    cin>>G.vexnum>>G.arcnum;
    for(i=;i<G.vexnum;i++)
    G.ver[i].first=NULL;
    for(k=;k<G.arcnum;k++)//输入一条边的两个端点
    {
        cin>>x>>y;
        p=new Arcnode;
        p->ad=y;p->next=G.ver[x].first;G.ver[x].first=p;
        p1=new Arcnode;
        p1->ad=x;p1->next=G.ver[y].first;G.ver[y].first=p1;
    }
}

void DFSAL(ALGraph G,int v)//一个连通分量的深度优先搜索遍历
{
    int w;
    cout<<v<<" ";visit[v]=true;
    Arcnode *p2;
    p2=new Arcnode;
    //输出第一个点，同时记录已经访问过
    p2=G.ver[v].first;
    while(p2)
    {
        w=p2->ad;
        if(!visit[w])     DFSAL(G,w);//对尚未访问过且与上一个顶点间存在边的顶点递归调用
        p2=p2->next;
    }
}

void DFS(ALGraph G)//非连通图的深度优先搜索遍历
{
    int v;
    for(v=;v<G.vexnum;v++)
        visit[v]=false;//标记数组初始化
    for(v=;v<G.vexnum;v++)
    {
        if(!visit[v])//对于未访问的顶点调用DFSAMG函数
        {    cout<<"{ ";
            DFSAL(G,v);
            cout<<"}"<<'\n';
        }
     }
} 

void BFSAL(ALGraph G,int v)//一个连通分量的广度优先搜索遍历
{
    queue<int> q;
    int w,x;
    cout<<v<<" ";//采用先访问再入队方法
    q.push(v);
    visit[v]=true;//入队第一个点，同时记录已经访问过
    while(!q.empty())//循环下面操作，直到队空
    {
        x=q.front();//记录此时队头顶点，再出队
        Arcnode *p3;
        p3=new Arcnode;
        p3=G.ver[x].first;
        q.pop();
        while(p3)
        {
            w=p3->ad;
            if(!visit[w])//若两点间有边且未访问
            {
                cout<<w<<" "; //输入此顶点
                visit[w]=true;//标记已经访问过
                q.push(w);//将此点入队
            }
            p3=p3->next;
        }
    }
}

void BFS(ALGraph G)//非连通图的深度优先搜索遍历
{
    int v;
    for(v=;v<G.vexnum;v++)
        visit[v]=false;//标记数组初始化
    for(v=;v<G.vexnum;v++)
    {
        if(!visit[v])//对于未访问的顶点调用DFSAMG函数
        {    cout<<"{ ";
            BFSAL(G,v);
            cout<<"}"<<'\n';
        }
     }
} 

int main()
{
    ALGraph g;
    create(g);
    DFS(g);
    BFS(g);
    return ;
}

这一章还有很多需要学习，这里只是对图的理解和最基础的的操作，后面许多算法还只停留在理解，实际应用还实现不了，接下来需要对图的应用那部分内容有更多的学习和探索。