Linear Regression 线性回归

Motivation 问题描述

收集到某一地区的房子面积和房价的数据（x, y）42组,对于一套已知面积的房子预测其房价？

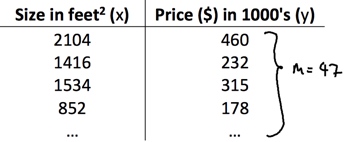
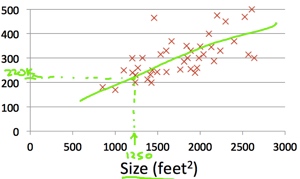
由房价数据可视化图可以看出，可以使用一条直线拟合房价。通过这种假设得到的预测值和真实值比较接近。

Model 模型

将现实的问题通过数学模型描述出来。
m 个样本(example)组成训练集(training set)，每一个样本有n个特征(feature)和一个标签(label)。目的是，通过一个数学模型(algorithm)和参数(parameters)将每一个样本和标签映射。这样，给定一个未知的样本就可以通过建立的数学模型预测其标签。

参数	解释
m	样例数 training set
n	特征数 no. of features
X	(m*(n+1))
y	(m*1)
$\Theta$	((n+1)*1) $X\theta=y$

Hypothesis 假设

假设房价由此方程拟合
\[h_\theta(x) = \theta_0+\theta_1x\]
其中$\theta_0$为偏置bias，$\theta_1$为因变量的权重weight

Cost function 损失函数

需要一个函数评价拟合函数的预测效果如何。直观的，我们可以计算真实房价和预测房价的差值平方和J，J越小预测效果越好。所以，可以通过最小化J可以求出参数$\theta_0$和$\theta_1$的值。
\[J(\theta_0,\theta_1)=\frac 1 {2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2\]

Gradient descent 梯度下降

这是一个二元函数求极值的问题。可以使用求偏导的方法找出所有极值点，然后代入损失函数求出最小值。一般的做法是采用梯度下降法。梯度下降选择一个系数alpha，和迭代次数。
repeat until convergence {
\[\theta_0 := \theta_0 - \alpha\frac 1 {2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\]
\[\theta_1 := \theta_1 - \alpha\frac 1 {2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\cdot{x^{(i)}}\]
}
下图是二维梯度下降可视化

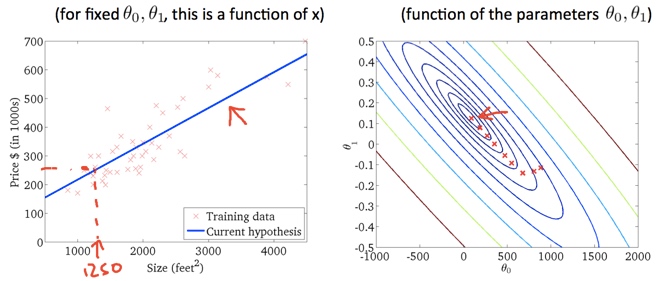
通过这种方式可以得出假设的参数。对于已知房子面积的房子就可以使用假设估计房价了。值得一提的是预测的房价不可能是100%准确，但是可以认为是在给定条件下最接近真实房价的值。
注意，梯度下降求的的只是极值点，有可能陷入局部最优，但是对于凸函数，极值点就是最值点，因为极值点只有一个。

LG with multiple variables 多元线性回归

更一般的情况是房价可能由多种因素综合决定，像房子年龄，卧室数目和楼层数。

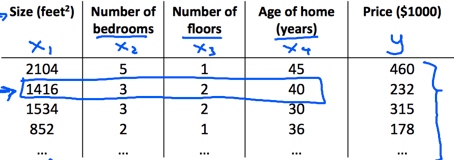
这时hypothesis变为
\[h_\theta = \theta_0 + \theta_1x_1 + \cdots + \theta_nx_n\]
cost function变为
\[J(\theta_0,\theta_1, \cdots ,\theta_n)=\frac 1 {2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2\] gradient descent变为
\[\theta_j := \theta_j - \alpha\frac 1 {2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\cdot{x^{(i)}_j}\]
注意使用feature scaling将不同范围的特征映射到相近的范围。

Polynomial regression多项式回归

更一般的情况是房价和面积是如下图的关系。解决方法转化为多元线性回归。

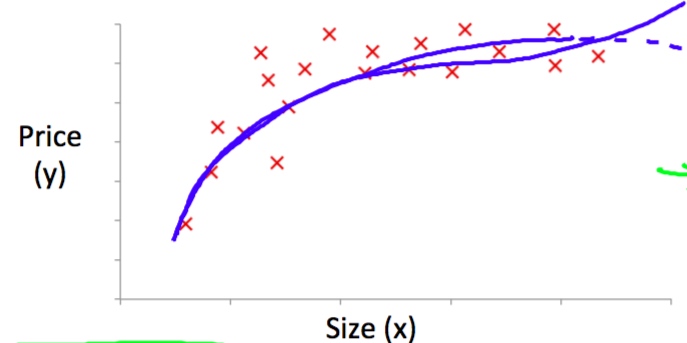
在这种情况下，一种可能是选择以下特征
\[x_1=size,x_2=(size)^2\]
hypothesis 为
\[h_\theta(x)=\theta_0+\theta_1(size)+\theta_2(size)^2\]
即为
\[h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2\]
通过这种方法就可以转换为多元线性回归问题。

Normal Equation

使用多元函数求极值的方法。只是以向量的方式表示。
当除了使用梯度下降外，还可以使用normal equation求参数。

\[X\theta=y\]
解得
\[\theta=(X^TX)^{-1}X^Ty\]
注意当features数多于样本数的情况
解决办法增加样本数，减少特征数，使用normalization

References