分类回归树（CART）

概要

本部分介绍 CART，是一种非常重要的机器学习算法。

 

---

基本原理

 

CART 全称为 Classification And Regression Trees，即分类回归树。顾名思义，该算法既可以用于分类还可以用于回归。

克服了 ID3 算法只能处理离散型数据的缺点，CART 可以使用二元切分来处理连续型变量。二元切分法，即每次把数据集切分成两份，具体地处理方法是：如果特征值大于给定值就走左子树，否则就走右子树。对 CART 稍作修改就可以处理回归问题。先前我们使用香农熵来度量集合的无组织程度，如果选用其它方法来代替香农熵，就可以使用树构建算法来完成回归。

本部分将构建两种树，第一种是回归树，其每个叶节点包含单个值；第二种是模型树，其每个叶节点包含一个线性方程。

 

---

回归树

要对树据的复杂关系建模，我们已经决定用树结构来帮助切分数据，那么如何实现数据的切分呢？怎么才能知道是否已经充分切分呢？这些问题的答案取决于叶节点的建模方式。回归树假设叶节点是常数值，需要度量出数据的一致性，在这里我们选择使用平方误差的总值来达到这一目的。

选择特征的伪代码如下：

对每个特征：
    对每个特征值：
        将数据切分成两份（二元切分）
             计算切分的误差（平方误差）
             如果当前误差小于当前最小误差，那么将当前切分设定为最佳切分并更新最小误差
返回最佳切分的特征和阈值

与 ID3 或 C4.5 唯一不同的是度量数据的一致性不同，前两者分别是信息增益和信息增益率，而这个是用平方误差的总值，有一点聚类的感觉。比如这样的数据集：

程序创建的树结构就是：

{'spInd': 0, 'spVal': 0.48813000000000001, 'left': 1.0180967672413792, 'right': -0.044650285714285719}

在分类树中最常用的是基尼指数：在分类问题中，假设有 \(K\) 个类，样本点属于第 \(k\) 类的概率为 \(p_k\)，则概率分布的基尼指数定义为

\begin{align}

Gini(p) = \sum_{k=1}^K p_k(1-p_k) = 1- \sum_{k=1}^K p_k^2

\end{align}

基尼系数与熵的特性类似，也是不确定性的一种度量。对于样本集合 \(D\)，基尼指数为

\begin{align}

Gini(D) = 1- \sum_{k=1}^K\left( \frac{\lvert C_k \rvert }{\lvert D \rvert} \right)

\end{align}

其中 \(C_k\) 是 \(D\) 中属于样本集合第 \(k\) 类的样本子集， \(K\) 是类的个数。

 

---

剪枝

一棵树如果节点过多，表明该模型可能对数据进行了“过拟合”。控制决策树规模的方法称为剪枝，一种是先剪枝， 一种是后剪枝。所谓先剪枝，实际上是控制决策树的生长，后剪枝是指对完全生成的决策树进行修剪。

先剪枝方法有：

• 数据划分法。划分数据成训练样本和测试样本，使用训练样本进行训练，使用测试样本进行树生长检验
• 阈值法。当某节点的信息增益小于某阈值时，停止树生长
• 信息增益的统计显著性分析。从已有节点获得的所有信息增益统计其分布，如果继续生长得到的信息增益与该分布相比不显著，则停止树的生长

先剪枝的优缺点

• 优点：简单直接
• 缺点：对于不回溯的贪婪算法，缺乏后效性考虑，可能导致树提前停止

 

后剪枝方法有：

• 减少分类错误修剪法。使用独立的剪枝集估计剪枝前后的分类错误率，基于此进行剪枝
• 最小代价与复杂性折中的剪枝。对剪枝后的树综合评价错误率和复杂性，决定是否剪枝
• 最小描述长度准则。最简单的树就是最好的树，对决策树进行编码，通过剪枝得到编码最小的树
• 规则后剪枝。将训练完的决策树转换成规则，通过删除不会降低估计精度的前提下修剪每一条规则

后剪枝的优缺点

• 优点：实际应用中有效
• 缺点：数据量大时，计算代价较大

 

下面讲述一种用于 CART 回归树的剪枝操作。一般使用后剪枝方法需要将数据集分成测试集和训练集，C4.5 所用的剪枝操作还是一种特殊的后剪枝操作，不需要测试集。

剪枝操作前，首先指定参数，使得构建出的树足够大、足够复杂，便于剪枝。接下来从上而下找到叶结点，用测试集来判断将这些叶节点合并是否能降低测试误差，如果是的话就合并。伪代码如下：

基于已有的树切分测试数据：
    如果存在任一子集是一棵树，则在该子集递归剪枝过程
    计算将当前两个叶节点合并后的误差
    计算不合并的误差
    如果合并会降低误差的话，就将叶节点合并

 

---

模型树

模型树仍然采用二元切分，但叶节点不再是简单的数值，取而代之的是一些线性模型。

考虑下图中的数据，显然两条直线拟合效果更好。

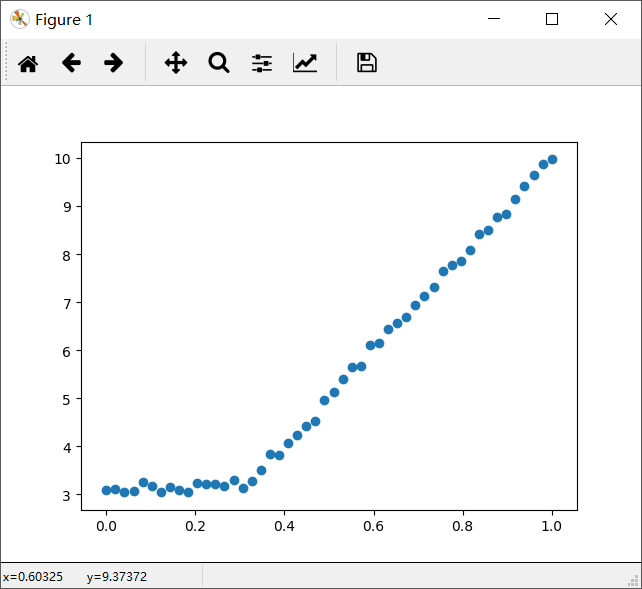
对回归树稍作修改就可以变成模型树。模型树的生成树关键在于误差的计算。对于给定的数据集，应该先用线性的模型对它进行拟合，然后计算真实的目标值与模型预测值间的差值。最后将这些差值的平方求和就得到了所需要的误差。

 

树回归优缺点

 

• 优点：可以对复杂和非线性的数据建模
• 缺点：结果不易理解