UVA 1599， POJ 3092 Ideal Path 理想路径 (逆向BFS跑层次图)

大体思路是从终点反向做一次BFS得到一个层次图，然后从起点开始依次向更小的层跑，跑的时候选则字典序最小的，由于可能有多个满足条件的点，所以要把这层满足条件的点保存起来，在跑下一层。跑完一层就会得到这层最小的color号。

反省：这道题由于有自环和重边的存在，因此满足条件的一个点可能多次被加到队列，这样的复杂度将会成指数级。没注意到这点TLE了几发。。。如果一个点到另一个点的最短路径只有一条，就不用判断重复了。正是因为重边所以特别需要注意这点

示意图：

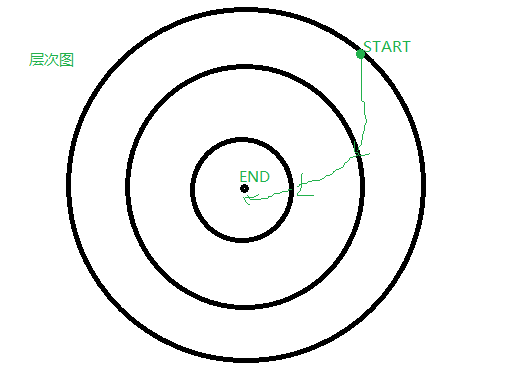
学习点：

1.层次图的构建，逆向思维。

2.注意不是简单图的情况，重边和自环。

3.搜索最致命的问题就是状态判重

#include<cstdio>
#include<cstring>
#include<vector>
#include<queue>

//#define local
using namespace std;
const int INF = 1e9;
const int maxm = 2e5 + ;
const int maxn = 1e5 + ;
int n;

struct Edge
{
   int v,c,nxt;
}e[maxm<<];

int d[maxn];
int cnt , head[maxn];

//init head -1
inline void addEdge(int u,int v,int c)
{
 //  e[cnt].u = u;
   e[cnt].v = v;
   e[cnt].c = c;
   e[cnt].nxt = head[u];
   head[u] = cnt++;
}

void bfs()
{
   queue<int> q;
   memset(d,-,sizeof(d));
   q.push(n); d[n] = ;
   int u,v,i;
   while(!q.empty()){
      u = q.front(); q.pop();
      if(u == ) { printf("%d\n",d[u]); return ;}
      for(i = head[u]; ~i ; i = e[i].nxt ){
         v = e[i].v;
         if(~d[v]) continue;
         d[v] = d[u] + ;
         q.push(v);
      }
   }
}

bool vis[maxn];
void bfs2()
{
   queue<int> q;///复杂度写高了 没有给结点判断重复 指数级
   int u = ,v, i;
   q.push(u);
   int c = INF;//最小color
   vector<int> vec;//保存下一个层次的点
   memset(vis,false,sizeof(vis));
   while(!q.empty()||!vec.empty()) {

      if(q.empty()) { //保证队列里只有一个层次的点，如果队列空了，说明上一层的点都跑完了，这时候c一定是最小的
         for(i = ;i < vec.size();i++) {
            int k = vec[i], v = e[k].v;
            if(e[k].c == c && !vis[v] ) {//vis[v] 重边
               if(e[k].v == n) { printf("%d\n",c); return ;}
               q.push(e[vec[i]].v); vis[v] = true;
            }
         }
         vec.clear();
         printf("%d ",c); c = INF;
      }

      u = q.front(); q.pop();

      for(i = head[u]; ~i ; i = e[i].nxt ) {
         v = e[i].v;
         if(d[u] - d[v] ==  && e[i].c <= c) {
            vec.push_back(i);
            c = e[i].c;
         }
      }
   }
}

int main()
{
#ifdef local
    freopen("in.txt","r",stdin);
#endif // local
   int m;
   int u,v,c;
   while(~scanf("%d%d",&n,&m)){
      memset(head,-,sizeof(head)); cnt = ;
      while(m--) {
         scanf("%d%d%d",&u,&v,&c);
         if(u == v) continue;//忽略自环
         addEdge(u,v,c);
         addEdge(v,u,c);
      }
      bfs();
      bfs2();
   }
   return ;
}