【原创】tarjan算法初步（强连通子图缩点）

【原创】tarjan算法初步（强连通子图缩点）

tarjan算法的思路不是一般的绕！！(不过既然是求强连通子图这样的回路也就可以稍微原谅了。。)

但是研究tarjan之前总得知道强连通分量是什么吧。。

上百度查查：

　　有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

看不懂。。那么——

看这张图

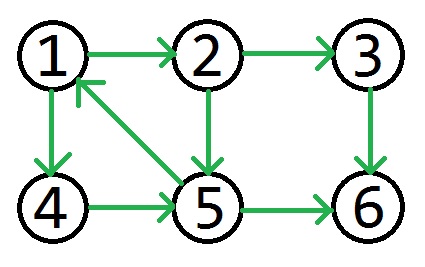
其中从1可以到2,3,4,5,6；

从2可以到1,3,4,5,6；

从3可以到6;

从4可以到1,2,3,5,6；

从5可以到1,2,3,4,6；

从6哪儿都到不了。

我们发现，{1,2,4,5}两两可以互达，我们称其为原图的一个强连通子图，而{3},{6}各自单独为原图的另外两个强连通子图。

我们想要通过程序实现O(n)求所有强连通子图，就要用到tarjan算法。

程序代码如下(tarjan的主要思路写在程序注释里，若无法理解请参考另一篇【转载】全网最!详!细!tarjan算法讲解)：

 // Tarjan有向图强连通缩点
 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<iostream>
 #include<string>
 #define MAXV 10010
 #define MAXE 100010
 using namespace std;
 struct tEdge{
     int np;
     tEdge *next;
 }E[MAXE],*V[MAXV];
 int tope=-;
 int n,m;
 int dfn[MAXV],dfstime=;  // dfn[i]表示点i的dfs序
 int low[MAXV];  // low[i]表示目前点i所能到达的最小dfs序点
 int status[MAXV];  // status[i]表示点i的访问状态,0=未访问,1=访问中,2=访问完毕
 int stack[MAXV],tops=-;
 int color[MAXV],totc=;  // color[]表示缩点后的块
 void addedge(int u,int v){
     E[++tope].np=v;
     E[tope].next=V[u];
     V[u]=&E[tope];
 }
 void tarjan(int now){
     stack[++tops]=now;  // 进栈
     low[now]=dfn[now]=++dfstime;  // 初始化dfs序
     status[now]=;  // 访问中(在栈中)
     for(tEdge *ne=V[now];ne;ne=ne->next){
         if(status[ne->np]==){  // 未访问(没有进过栈)
             tarjan(ne->np);  // dfs往下进行递归访问
             low[now]=min(low[now],low[ne->np]);
             // 由于now可达ne->np,故ne->np可达的最小dfs序点从now也可达
         }
         else if(status[ne->np]==){  // 回边,发现ne->np为栈中元素
             low[now]=min(low[now],dfn[ne->np]);
             // 若ne->np的dfs序比原来now可达的最小dfs序还小则更新
         }
     }
     if(low[now]==dfn[now]){
         // now到达的最小dfs序为自己dfs序
         // 即now不包含在最小dfs序更小的缩点中
         // 而栈中now以后的节点若不能到达now则早已出栈(FILO)
         totc++;  // 申请新颜色(一种颜色代表一个缩点)
         while(stack[tops+]!=now){  // 栈中所有在now之后的节点都在该缩点内
             status[stack[tops]]=;  // 访问完毕(已出栈)
             color[stack[tops--]]=totc;  // 为节点染色
         }
     }
 }
 int main(){
     memset(dfn,,sizeof(dfn));
     memset(low,,sizeof(low));
     memset(status,,sizeof(status));
     scanf("%d%d",&n,&m);
     for(int i=;i<=m;i++){
         int u,v;
         scanf("%d%d",&u,&v);
         addedge(u,v);
     }
     for(int i=;i<=n;i++)
         if(status[i]==)
             tarjan(i);  // 图不连通时必须保证每个点都处理到
     for(int i=;i<=n;i++)
         printf("Point %d colored %d\n",i,color[i]);  // 输出所属强连通块编号
     return ;
 }

测试数据：

运行结果：

Point  colored
Point  colored
Point  colored
Point  colored
Point  colored
Point  colored 

即color[1]={6},color[2]={3},color[3]={1,2,4,5}为原图的3个强连通子图的缩点。